LiveCharts 概述

LiveCharts是一个比较漂亮的WPF图表控件，在数据变化时还会有动画切换的效果，并且样式也可以控制。

在这里插入图片描述

安装 LiveCharts 及如何使用

首先，点击项目，然后右键，选择 “管理NuGet程序包”

在这里插入图片描述
然后，搜索liveCharts，选择wpf版本的进行安装

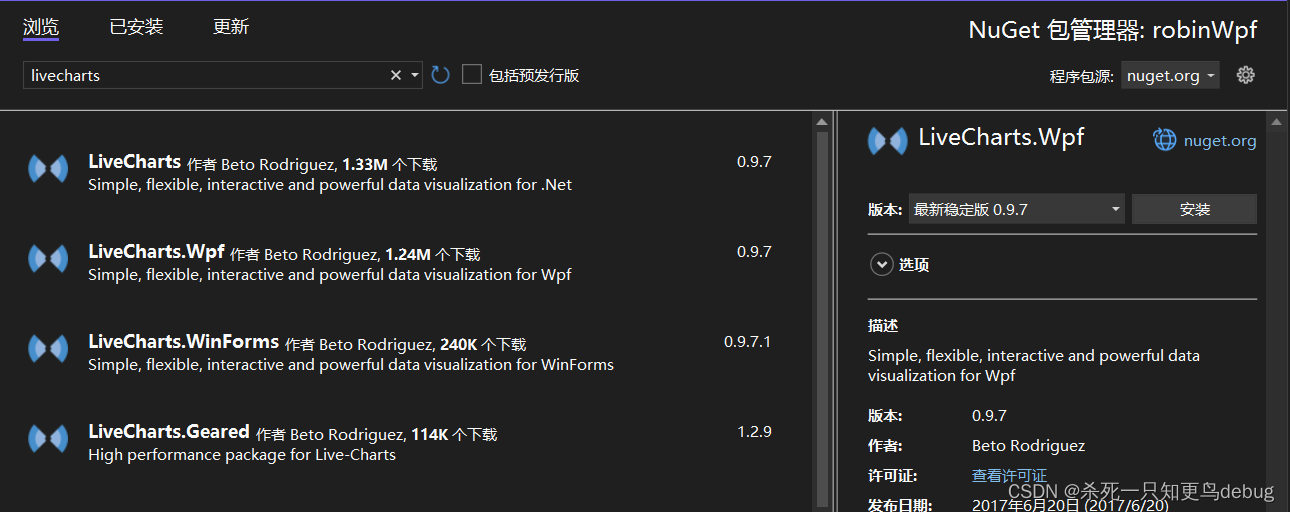
在这里插入图片描述

在需要使用liveCharts第三方库的xmal文件中，引入xmlns命名空间

 xmlns:lvc="clr-namespace:LiveCharts.Wpf;assembly=LiveCharts.Wpf"

直方图 LineSeries 属性说明

常用属性概览：
LegendLocation：" Top | Bottom | Left | Right " 设置图例的位置
Background 设置图表的背景色

LineSeries
a. Values : 设置线条的序列数据（数字序列）
b. Title : 设置线条的名称（作用于图例上面）
c. Fill : 用来填充线条下方数据区域的颜色（颜色值）
d. PointGeometry 设置数据点的形状
e. PointGeometrySize ：用来设置线条的点大小（数字值）
f. Stroke：设置线条的颜色（颜色值）
g. ForeGround：设置数据点字体的颜色（颜色值）
h. StrokeDashArray：设置线条虚线，数字值越大越虚
i. LineSmoothness 设置线条是否弯曲（0 或 1）0 为直线，1为曲线

AxisX （AxisY）
a. title 设置横纵轴标题（字符串）
b. Labels 设置横纵轴的标签（字符串）
c. LabelsRotation 设置坐标轴标签旋转的角度（数字值）
d. LabelFormatter 自定义坐标轴显示格式
e. ShowLabels 设置横纵轴的刻度是否显示（ True | False ）

综合直方图小例子

效果显示：

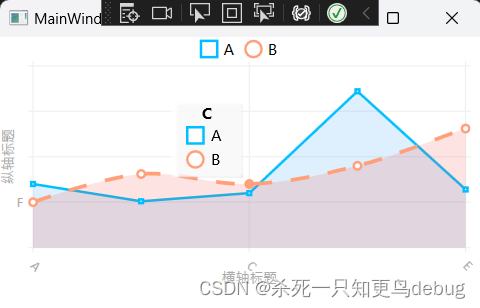
在这里插入图片描述

<lvc:CartesianChart  LegendLocation="Top" Background="white">
    <lvc:CartesianChart.Series>
        <!-- 直线实线 -->
        <lvc:LineSeries Values="20,1,10,122,14"  Stroke="DeepSkyBlue"  PointGeometrySize="5" Title="A" Foreground="Black"
                        LineSmoothness="0">
            <!-- 设置数据点的形状 -->
            <lvc:LineSeries.PointGeometry>
                <GeometryGroup>
                    <RectangleGeometry Rect="50,50,25,25" />
                </GeometryGroup>
            </lvc:LineSeries.PointGeometry>
        </lvc:LineSeries>
        <!-- 曲线虚线 -->
        <lvc:LineSeries Values="0,31,20,40,81"  Stroke="LightSalmon"  PointGeometrySize="8" Title="B"  StrokeDashArray="5"/>
    </lvc:CartesianChart.Series>
    <!-- 图表的横轴设置-->
    <lvc:CartesianChart.AxisX> 
        <lvc:Axis Title="横轴标题" Labels="A,B,C,D,E" LabelsRotation="45"/>
    </lvc:CartesianChart.AxisX>
    <!-- 图表的纵轴设置-->
    <lvc:CartesianChart.AxisY>
        <lvc:Axis Title="纵轴标题" Labels="F,G,H,I,J"/>
    </lvc:CartesianChart.AxisY>
</lvc:CartesianChart>