文章目录
- 动态规划(两个数组问题)
- 1. 最长公共子序列
- 2. 不相交的线
- 3. 不同的子序列
- 4. 交错字符串
- 5. 两个字符串的最小ASCII和
- 6. 最长重复子数组
- 7. 通配符匹配
动态规划(两个数组问题)
1. 最长公共子序列
题目链接
-
状态表示
dp[i][j] 表示 s1 0 到 i 区间内,以及时s2 0 到 j 区间内所有的子序列中,最长的公共子序列 -
状态转移方程
根据最后一个位置的请款分类讨论。
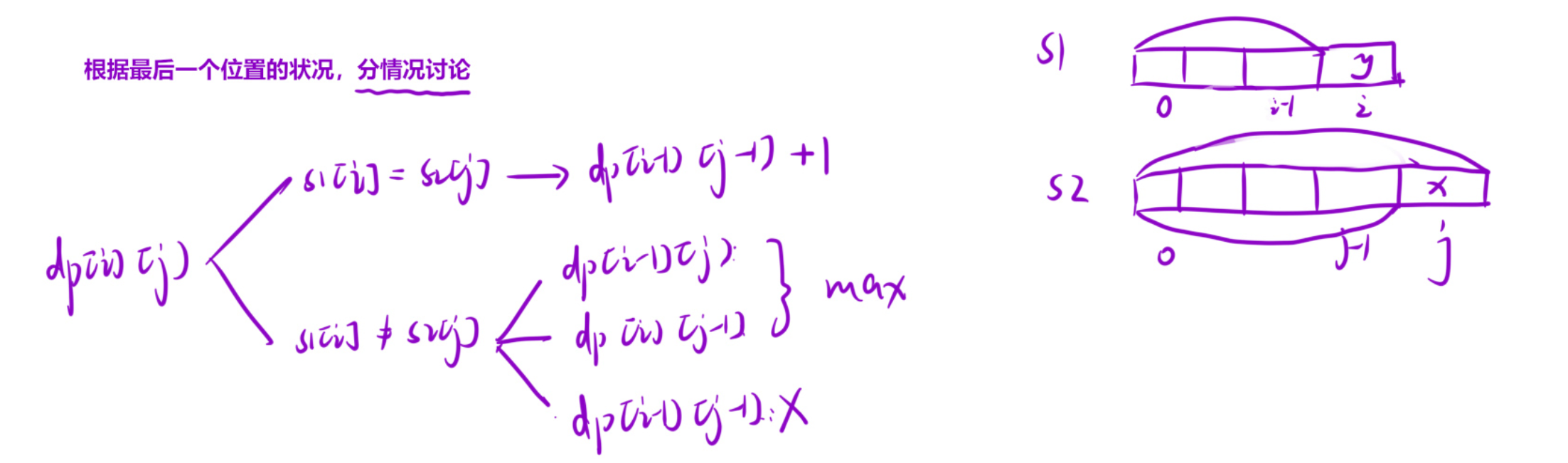
-
初始化
关于字符串的dp问题,空串是有研究意义的。引入空串的概念之后会方便我们的初始化
这里还可以使用之前的方法,使用辅助节点的方式
-
填表顺序
从下往上,从左到右
-
返回值
AC代码:
class Solution
{
public:
int longestCommonSubsequence(string text1, string text2)
{
int n = text1.size();
int m = text2.size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[n][m];
}
};
2. 不相交的线
题目链接
题目分析:根据这个题目可以看到不就是找最长公共子序列嘛
-
状态表示
dp[i][j] 表示 0 到 i 的所有子序列以及 0 到 j 的所有子序列当中,最长的公共子序列 -
状态转移方程
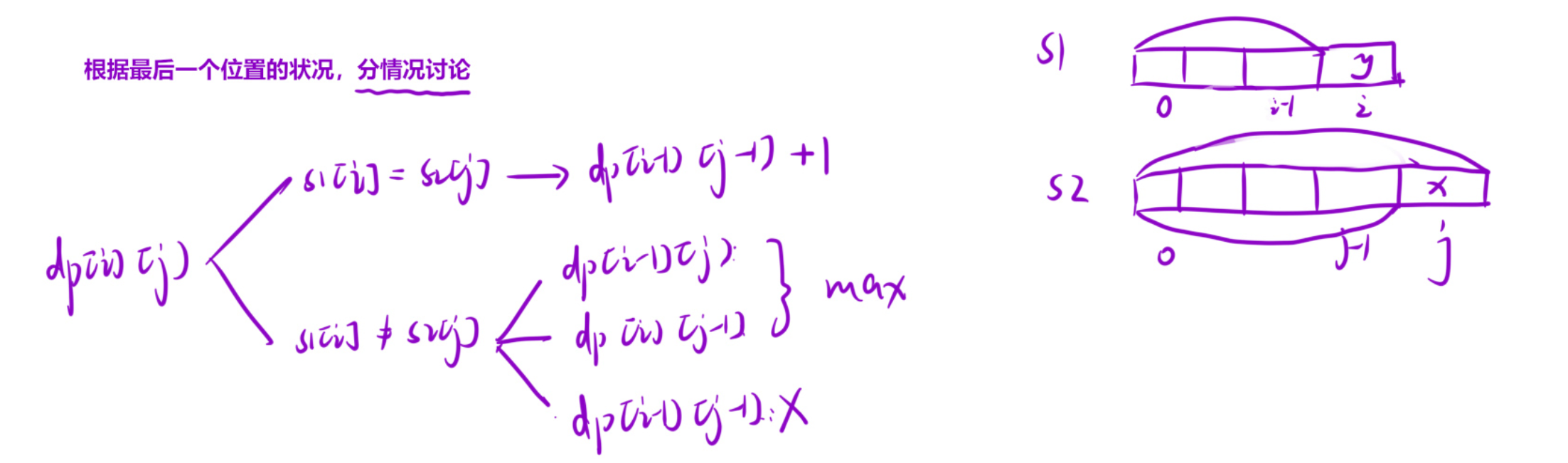
-
初始化
-
填表
-
返回值
AC代码:
class Solution
{
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2)
{
int n = nums1.size();
int m = nums2.size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[n][m];
}
};
3. 不同的子序列
题目链接
-
状态表示
dp[i][j] 表示 0 到 j 之间的所有子序列中有多少个出现 目标中0 到 i 之间的字母 -
状态转移方程

-
初始化
-
填表
-
返回值
AC代码:
class Solution
{
public:
int numDistinct(string s, string t)
{
int n = s.size();
int m = t.size();
vector<vector<double>> dp(m + 1, vector<double>(n + 1));
for (int i = 0; i <= n; i++) dp[0][i] = 1;
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
dp[i][j] += dp[i][j - 1];
if (s[j - 1] == t[i - 1]) dp[i][j] += dp[i - 1][j - 1];
}
}
return dp[m][n];
}
};
4. 交错字符串
题目链接
-
状态表示
dp[i][j] 表示 s1中[1, i]之间的字符串,以及s2当中[1,j]之间的字符串能否拼接成s3当中[1, i + j]之间的字符串 -
状态转移方程

-
初始化
当两个字符串都是空的时候,返回的一定是true,当s1 不为空, s2 为空,只要s1有一个不等于s3则直接返回false否则为true
s2的初始化也一样
-
填表
从上到下,从左到右
-
返回值
AC代码:
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
int m = s1.size();
int n = s2.size();
if (m + n != s3.size()) return false;
s1 = " " + s1;
s2 = " " + s2;
s3 = " " + s3;
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = true;
for (int i = 1; i <= n; i++)
{
if (s2[i] == s3[i]) dp[0][i] = true;
else break;
}
for (int i = 1; i <= m; i++)
{
if (s1[i] == s3[i]) dp[i][0] = true;
else break;
}
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if ((s1[i] == s3[i + j] && dp[i - 1][j]) || (s2[j] == s3[i + j] && dp[i][j - 1]))
dp[i][j] = true;
}
}
return dp[m][n];
}
};
5. 两个字符串的最小ASCII和
题目链接
-
状态表示
分析,这个题目要找两个字符串最小的,可以找到公共最大的然后反向求
dp[i][j] 表示 [0, i] 以及[0, j]的所有子序列当中,ASCII最大的公共子序列的和 -
状态转移方程

-
初始化
无需初始化
-
填表
从左到右,从上到下
-
返回值
两个字符串的和前去最大的乘以2
AC代码:
class Solution
{
public:
int minimumDeleteSum(string s1, string s2)
{
int m = s1.size();
int n = s2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
if (s1[i - 1] == s2[j - 1])
{
dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + s1[i - 1]);
}
}
}
int sum = 0;
for (auto e : s1) sum += e;
for (auto e : s2) sum += e;
return sum - dp[m][n] - dp[m][n];
}
};
6. 最长重复子数组
题目链接
-
状态表示
dp[i][j]以 i 位置为结尾的所有子数组,以及以j 位置为结尾的所有子数组当中,最长公共子数组的长度 -
状态转移方程
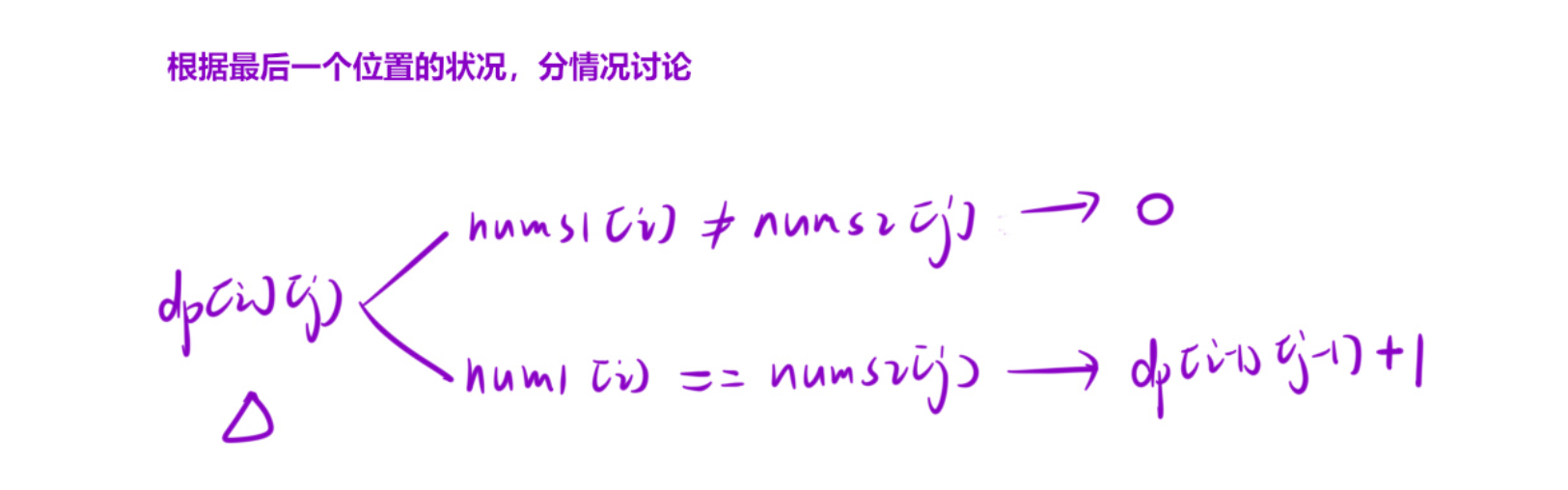
-
初始化
无需初初始化
-
填表
-
返回值
AC代码:
class Solution
{
public:
int findLength(vector<int>& nums1, vector<int>& nums2)
{
int m = nums1.size();
int n = nums2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
int ret = 0;
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (nums1[i - 1] == nums2[j - 1])
{
dp[i][j] = dp[i - 1][j - 1] + 1;
}
ret = max(ret, dp[i][j]);
}
}
return ret;
}
};
7. 通配符匹配
题目链接
-
状态表示
dp[i][j] 表示 p[0, j]区间内子串能否匹配s[0, i]区间内的子串 -
状态转移方程

这种有很多表示方法的状态转移方程,需要优化不可能把每个状态都表示出来
第一种就是采用数学方法来优化:
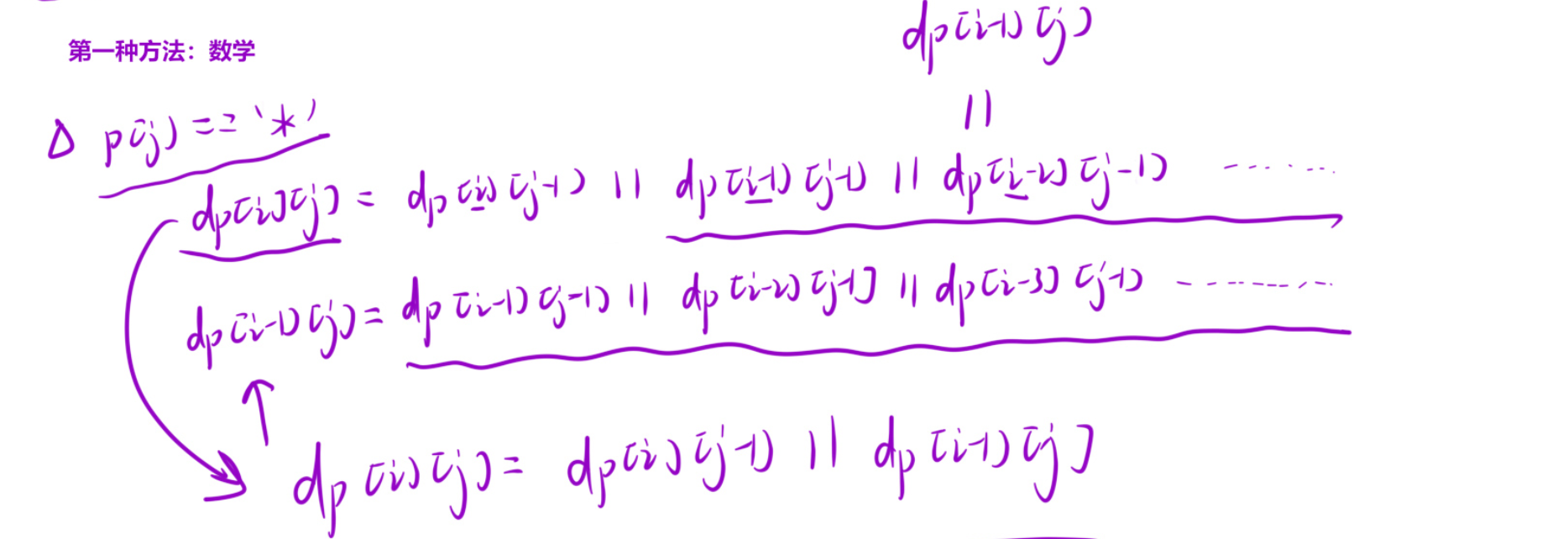
还可以根据状态表示以及实际情况优化状态转移方程

-
初始化
当
p[0][j] == ”*“时就一直是true -
填表
-
返回值
AC代码:
class Solution
{
public:
bool isMatch(string s, string p)
{
int m = s.size();
int n = p.size();
s = " " + s, p = " " + p;
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = true;
for (int j = 1; j <= n; j++)
{
if (p[j] == '*') dp[0][j] = true;
else break;
}
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (p[j] == '*')
dp[i][j] = dp[i- 1][j] || dp[i][j - 1];
else if (p[j] == '?') dp[i][j] = dp[i - 1][j - 1];
else
{
if (s[i] == p[j]) dp[i][j] = dp[i - 1][j - 1];
}
}
}
return dp[m][n];
}
};
{
if (p[j] == '*')
dp[i][j] = dp[i- 1][j] || dp[i][j - 1];
else if (p[j] == '?') dp[i][j] = dp[i - 1][j - 1];
else
{
if (s[i] == p[j]) dp[i][j] = dp[i - 1][j - 1];
}
}
}
return dp[m][n];
}
};