一【题目类别】

二【题目难度】

简单

三【题目编号】

572.另一棵树的子树

四【题目描述】

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

五【题目示例】

示例 1：
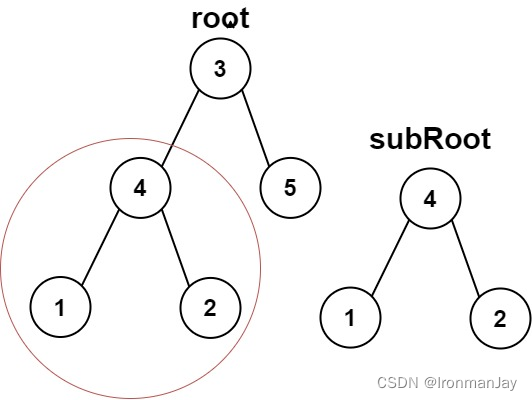
- 输入：root = [3,4,5,1,2], subRoot = [4,1,2]
- 输出：true
示例 2：
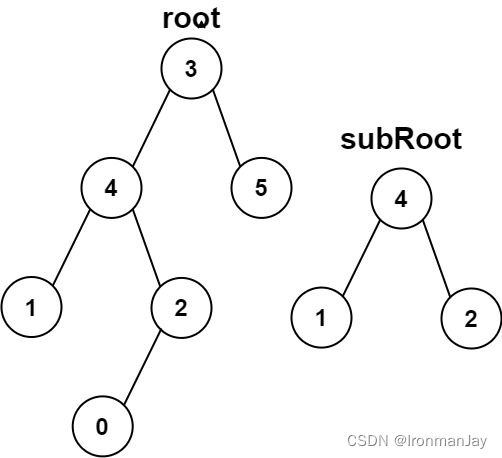
- 输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
- 输出：false

六【解题思路】

利用深度优先搜索
从root（主树）的根节点开始判断，subRoot（子树）是否是主树的子树
通过遍历整个root（主树）找新的根节点，来判断是否存在subRoot（子树）
是否是subRoot（子树）的判断比较简单，先看对应位置是否存在节点，再看节点值是否相同，具体可见代码
最后返回结果即可

七【题目提示】

$r o o t 树上的节点数量范围是 [1, 2000]$
$s u b R o o t 树上的节点数量范围是 [1, 1000]$
$10^4 <= root.val <= 10^4$
$10^4 <= subRoot.val <= 10^4$

八【时间频度】

时间复杂度： $O (m \times n)$ ，其中 $m 、 n$ 分别为两个树的节点个数
空间复杂度： $O(max\{d_m,d_n\})$ ，其中 $d_m、d_n$ 分别为两个树的高度，也就是递归栈的深度

九【代码实现】

Java语言版

public boolean isSubtree(TreeNode root, TreeNode subRoot) {
    if(judge(root,subRoot) || subRoot == null){
        return true;
    }
    if(root == null){
        return false;
    }
    return isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot);
}

public boolean judge(TreeNode p,TreeNode q){
    if(p == null && q == null){
        return true;
    }else if(p == null || q == null){
        return false;
    }else if(p.val != q.val){
        return false;
    }
    return judge(p.left,q.left) && judge(p.right,q.right);
}

C语言版

bool judge(struct TreeNode* p,struct TreeNode* q)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }
    else if(p == NULL || q == NULL)
    {
        return false;
    }
    else if(p->val != q->val)
    {
        return false;
    }
    return judge(p->left,q->left) && judge(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(judge(root,subRoot) || subRoot == NULL)
    {
        return true;
    }
    if(root == NULL)
    {
        return false;
    }
    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}