K均值聚类是一种常用的无监督学习算法,用于将一组数据点分成不同的簇(clusters),以便数据点在同一簇内更相似,而不同簇之间差异较大。K均值聚类的目标是通过最小化数据点与所属簇中心之间的距离来形成簇。
当我们要预测的是一个离散值时,做的工作就是“分类”。例如,要预测一个孩子能否成为优秀的运动员,其实就是要将他分到“好苗子”(能成为优秀的运动员)或“普通孩子”(不能成为优秀运动员)的类别。当我们要预测的是一个连续值时,做的工作就是“回归”。
例如,预测一个孩子将来成为运动员的指数,计算得到的是 0.99 或者 0.36 之类的数值。机器学习模型还可以将训练集中的数据划分为若干个组,每个组被称为一个“簇(cluster)”。
这些自动形成的簇,可能对应着不同的潜在概念,例如“篮球苗子”、“长跑苗子”。这种学习方式被称为“聚类(clusting)”,它的重要特点是在学习过程中不需要用标签对训练样本进行标注。也就是说,学习过程能够根据现有训练集自动完成分类(聚类)。
根据训练数据是否有标签,我们可以将学习划分为监督学习和无监督学习。
前面介绍的 K近邻、支持向量机都是监督学习,提供有标签的数据给算法学习,然后对数据分类。而聚类是无监督学习,事先并不知道分类标签是什么,直接对数据分类。
举一个简单的例子,有 100 粒豆子,如果已知其中 40 粒为绿豆,40 粒为大豆,根据上述标签,将剩下的 20 粒豆子划分为绿豆和大豆则是监督学习。
针对上述问题可以使用 K 近邻算法,计算当前待分类豆子的大小,并找出距离其最近的 5 粒豆子的大小,判断这 5 粒豆子中哪种豆子最多,将当前豆子判定为数量最多的那一类豆子类别。
同样,有 100 粒豆子,我们仅仅知道这些豆子里有两个不同的品种,但并不知道到底是什么品种。此时,可以根据豆子的大小、颜色属性,或者根据大小和颜色的组合属性,将其划分为两个类型。在此过程中,我们没有使用已知标签,也同样完成了分类,此时的分类是一种无监督学习。
聚类是一种无监督学习,它能够将具有相似属性的对象划分到同一个集合(簇)中。聚类方法能够应用于所有对象,簇内的对象越相似,聚类算法的效果越好。
理论基础
本节首先用一个实例来介绍 K 均值聚类的基本原理,在此基础上介绍 K 均值聚类的基本步骤,最后介绍一个二维空间下的 K 均值聚类示例。
分豆子
假设有 6 粒豆子混在一起,我们可以在不知道这些豆子类别的情况下,将它们按照直径大小划分为两类。
经过测量,以 mm(毫米)为单位,这些豆子的直径大小分别为 1、2、3、10、20、30。下面将它们标记为 A、B、C、D、E、F,并进行分类操作。
第 1 步:随机选取两粒参考豆子。例如,随机将直径为 1mm 的豆子 A 和直径为 2 mm 的豆子 B 作为分类参考豆子。
第 2 步:计算每粒豆子的直径距离豆子 A 和豆子 B 的距离。距离哪个豆子更近,就将新豆子划分在哪个豆子所在的组。使用直径作为距离计算依据时,计算结果如表 22-1 所示。

在本步骤结束时,6 粒豆子被划分为以下两组。
- 第 1 组:只有豆子 A。
- 第 2 组:豆子 B、C、D、E、F,共 5 粒豆子。
第 3 步:分别计算第 1 组豆子和第 2 组豆子的直径平均值。然后,将各个豆子按照与直径
平均值的距离大小分组。
- 计算第 1 组豆子的平均值 AV1 = 1mm。
- 计算第 2 组豆子的平均值 AV2 = (2+3+10+20+30)/5 = 13mm。
得到上述平均值以后,对所有的豆子再次分组:
- 将平均值 AV1 所在的组,标记为 AV1 组。
- 将平均值 AV2 所在的组,标记为 AV2 组。
计算各粒豆子距离平均值 AV1 和 AV2 的距离,并确定分组,如表 22-2 所示。
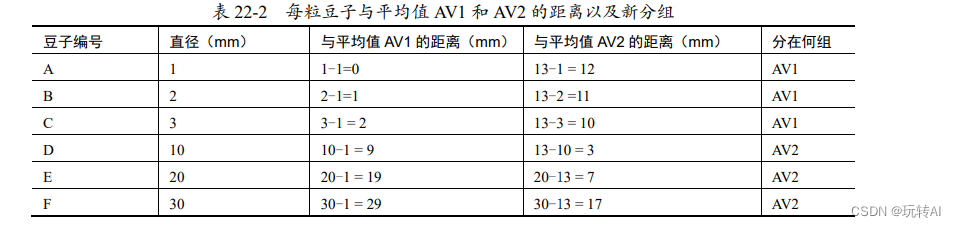
距离平均值 AV1 更近的豆子,就被划分为 AV1 组;距离平均值 AV2 更近的豆子,就被划分为 AV2 组。现在,6 粒豆子的分组情况为:
- AV1 组:豆子 A、豆子 B、豆子 C。
- AV2 组:豆子 D、豆子 E、豆子 F。
第4 步:重复第 3 步,直到分组稳定不再发生变化,即可认为分组完成。
在本例中,重新计算 AV1 组的平均值 AV41、AV2 组的平均值 AV42,依次计算每个豆子与平均值 AV41 和 AV42 的距离,并根据该距离重新划分分组。按照与第 3 步相同的方法,重新计算平均值并分组后,6 粒豆子的分组情况为:
- AV41 组:豆子 A、豆子 B、豆子 C。
- AV42 组:豆子 D、豆子 E、豆子 F。
与上一次的分组相比,并未发生变化,我们就认为分组完成了。
我们将直径较小的那一组称为“小豆子”,直径较大的那一组称为“大豆子”。
当然,本例是比较极端的例子,数据很快就实现了收敛,在实际处理中可能需要进行多轮的迭代才能实现数据的收敛,分类不再发生变化。
K 均值聚类函数
OpenCV 提供了函数 cv2.kmeans()来实现 K 均值聚类。该函数的语法格式为:
retval, bestLabels, centers=cv2.kmeans(data, K, bestLabels, criteria,
attempts, flags)
式中各个参数的含义为:
-
data:输入的待处理数据集合,应该是 np.float32 类型,每个特征放在单独的一列中。
-
K:要分出的簇的个数,即分类的数目,最常见的是 K=2,表示二分类。
-
bestLabels:表示计算之后各个数据点的最终分类标签(索引)。实际调用时,参数bestLabels 的值设置为 None。
-
criteria:算法迭代的终止条件。当达到最大循环数目或者指定的精度阈值时,算法停止继续分类迭代计算。该参数由 3 个子参数构成,分别为 type、max_iter 和 eps。
type 表示终止的类型,可以是三种情况,分别为:- cv2.TERM_CRITERIA_EPS:精度满足 eps 时,停止迭代。
- cv2.TERM_CRITERIA_MAX_ITER:迭代次数超过阈值 max_iter 时,停止迭代。
- cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER:上述两个条件中的
任意一个满足时,停止迭代。
-
max_iter:最大迭代次数。
-
eps:精确度的阈值。
-
attempts:在具体实现时,为了获得最佳分类效果,可能需要使用不同的初始分类值进
行多次尝试。指定 attempts 的值,可以让算法使用不同的初始值进行多次(attempts 次)
尝试。 -
flags:表示选择初始中心点的方法,主要有以下 3 种。
- cv2.KMEANS_RANDOM_CENTERS:随机选取中心点。
- cv2.KMEANS_PP_CENTERS:基于中心化算法选取中心点。
- cv2.KMEANS_USE_INITIAL_LABELS:使用用户输入的数据作为第一次分类中心点;
如果算法需要尝试多次(attempts 值大于 1 时),后续尝试都是使用随机值或者半随
机值作为第一次分类中心点。
返回值的含义为:
-
retval:距离值(也称密度值或紧密度),返回每个点到相应中心点距离的平方和。
-
bestLabels:各个数据点的最终分类标签(索引)。
-
centers:每个分类的中心点数据。
示例:有一堆米粒,按照长度和宽度对它们分类。
为了方便理解,假设米粒有两种,其中一种是 XM,另外一种是 DM。它们的直径不一样,XM 的长和宽都在[0, 20]内,DM 的长和宽都在[40, 60]内。使用随机数模拟两种米粒的长度和宽度,并使用函数 cv2.kmeans()对它们分类。
根据题目要求,主要步骤如下:
(1)随机生成两组米粒的数据,并将它们转换为函数 cv2.kmeans()可以处理的形式。
(2)设置函数 cv2.kmeans()的参数形式。
(3)调用函数 cv2.kmeans()。
(4)根据函数 cv2.kmeans()的返回值,确定分类结果。
(5)绘制经过分类的数据及中心点,观察分类结果。
代码如下:
import numpy as np
import cv2
from matplotlib import pyplot as plt
# 随机生成两组数值
# xiaomi 组,长和宽都在[0,20]内
xiaomi = np.random.randint(0,20,(30,2))
#dami 组,长和宽的大小都在[40,60]
dami = np.random.randint(40,60,(30,2))
# 组合数据
MI = np.vstack((xiaomi,dami))
# 转换为 float32 类型
MI = np.float32(MI)
# 调用 kmeans 模块
# 设置参数 criteria 值
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
# 调用 kmeans 函数
ret,label,center=cv2.kmeans(MI,2,None,criteria,10,cv2.KMEANS_RANDOM_CENTERS)
'''
#打印返回值
print(ret)
print(label)
print(center)
'''
# 根据 kmeans 的处理结果,将数据分类,分为 XM 和 DM 两大类
XM = MI[label.ravel()==0]
DM = MI[label.ravel()==1]
# 绘制分类结果数据及中心点
plt.scatter(XM[:,0],XM[:,1],c = 'g', marker = 's')
plt.scatter(DM[:,0],DM[:,1],c = 'r', marker = 'o')
plt.scatter(center[0,0],center[0,1],s = 200,c = 'b', marker = 'o')
plt.scatter(center[1,0],center[1,1],s = 200,c = 'b', marker = 's')
plt.xlabel('Height'),plt.ylabel('Width')
plt.show()
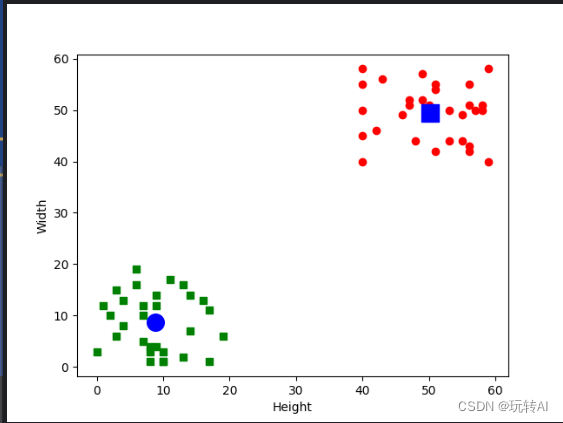
右上方的小方块是标签为“0”的数据点,左下方的圆点是标签为“1”的
数据点。右上方稍大的圆点是标签“0”的数据组的中心点;左下方稍大的方块是标签为“1”的数据组的中心点。








![[C++] 迭代器失效示例](https://img-blog.csdnimg.cn/0722629f7a69499599216f0327597092.png)