题目

---

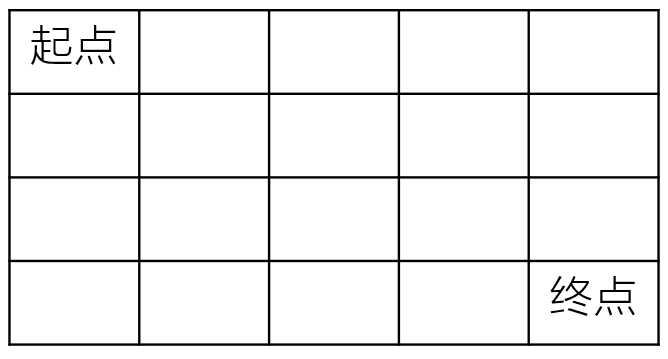
一个机器人在m×n大小的地图的左上角（起点）。
机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。
可以有多少种不同的路径从起点走到终点？

数据范围：0<n,m≤100，保证计算结果在32位整型范围内
要求：空间复杂度 O(nm)，时间复杂度 O(nm)
进阶：空间复杂度 O(1)，时间复杂度 O(min(n,m))

示例1

输入：
2,1
返回值：
1

示例2

输入：
2,2
返回值：
2

思路

---

这题属于动态规划，可以用递归解决，每次n∗m矩阵的子问题都是(m−1)∗n的矩阵与m∗(n−1)的矩阵的和。

解答代码

---

class Solution {
public:
    /**
     * @param m int整型 
     * @param n int整型 
     * @return int整型
     */
    int uniquePaths(int m, int n) {
        // write code here
        if (m ==1 || n == 1) {
            return 1;
        }
        return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
    }
};