优化与优化库

优化问题

👉优化问题组成

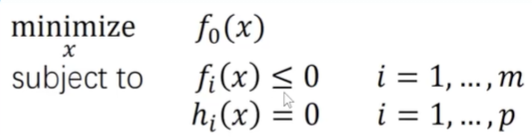
优化对象+目标函数/损失函数/评价函数+约束条件

👉分类
可以分为凸优化和非凸优化
什么是凸优化呢？

• 目标函数是凸的（有单一极值点称为是凸的）
• 不等式约束是凸的
• 所在的空间是凸的
• 等式约束是仿射形式
  常见形式
  

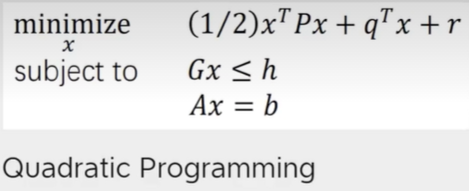
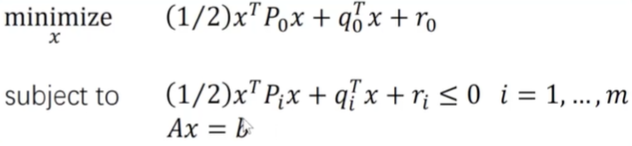
非凸优化

只要不是凸的，那就是非凸

👉数据来源
批量式betch：一次性给定一批观测数据
增量式incremental:数据是随着时间逐渐采集的
难点是如何根据后面的数据调整之前的估计结果

👉优化对象
合理选择优化对象：
关于优化对象的选择，在SLAM中可以选择优化对象是位置、姿态、传感器参数等
机器人抽象量（上位机）： 优化对象可以是时间多项式轨迹、推力大小方向、移动速度、转向角等
执行器底层量（下机位）：优化对象可以是电机转速和舵机转角
维度削减：
👉目标函数
目标函数的选择与要处理的问题密切相关
前端路径点搜索
后端优化生成轨迹
轨迹跟踪
👉约束条件
无约束优化一般来说会比有约束优化更容易求解，我们很想把有约束优化化成无约束优化问题
我们可以把约束加在目标函数中（拉格朗日乘子法）
转换对象空间（三角换元，三角函数简化公式等）
👉问题求解

• 数值解：求导，找极值点
• 解析解：求梯度，找增量
  常见优化库：
• ceres:代码开源、用于求解具有边界约束的非线性最小二乘和一般无约束优化问题。
• g2o:代码开源、用于解决非线性最小二乘问题，特点是将优化中涉及的对象用图的形式来表示。
• gtsam:使用因子图和贝叶斯网络作为底层计算范式而不是稀疏矩阵来优化最可能的配置
• osqp:多位大牛联合开发，用来求解QP问题的解
• CVX：MATLAB封装包，内嵌多种优化库
• MOSEK：适合的问题多，学生可以免费用，无源代码，库仅支持x86
• GLKP：快速鲁棒LP求解器，代码开源
• OOQP:快速鲁棒QP求解器，代码开源
• casadi:
  学习资料：
  

非线性最小二乘问题

无约束最小二乘是优化问题
关于非线性，我们只需要将其在局部线性化就可以了，具体的求解方式，我们选择迭代求解（比较通用的方法，因为复杂问题通常是难以求出解析解的）
非线性最小二乘的求解是比较独立的模块，是解决非线性最小二乘问题的常用方法，并不是状态估计独有的。

非线性最小二乘求解方法

👉问题描述

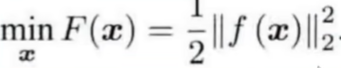
解析解：fx的形式复杂，不一定能求出解析解
数值解：

求解数值解的关键是：各个维度加还是减，加多少or减多少

👉直接方法
一阶梯度下降
二阶（牛顿法）：
仅使用一阶梯度作为下降方向，有时并不能很好的拟合函数的局部趋势

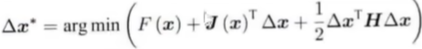
梯度下降方法过于贪心， 容易走出锯齿形路线
牛顿法中，海森矩阵H计算不易，求逆也不易