Roulettes

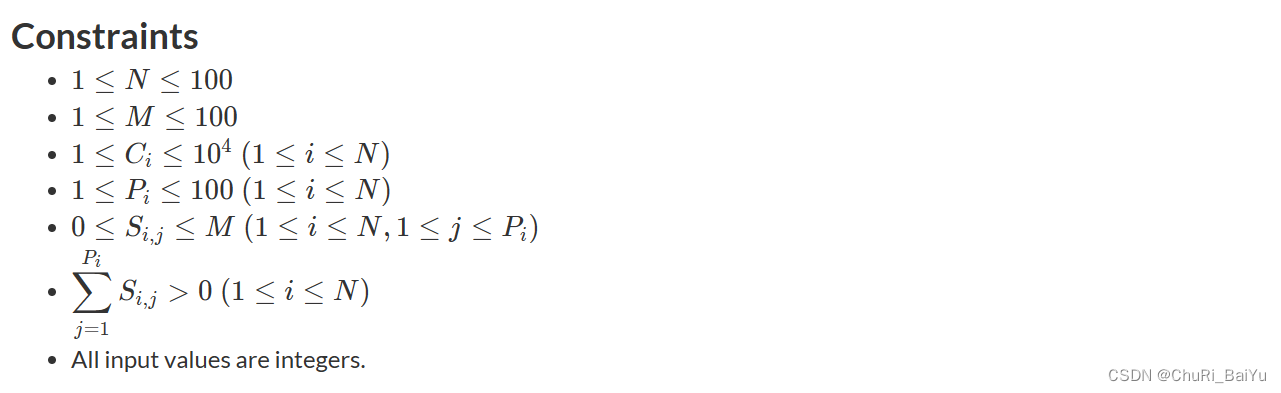
问题建模

给定n个轮盘，每个轮盘上有p个积分，每次转动轮盘需要一定的代价，在转动轮盘后可以等概率获得p个积分中的一个，每个轮盘可以转任意次。问获得m个积分所需的最小代价为多少。

问题分析

1.分析每个转盘对所求的作用

每个转盘，每转一次，可以等概率获得转盘内的一个积分，所求为m点积分，则转盘内的每一个积分对每个点的积分都有一定概率的贡献。

2.从集合的角度思考每个积分的贡献

考虑维护1~m点积分的集合内所需的最小代价，对于每一个轮盘内的积分加入后更新对应所需。设$$f(i)$$为积分大于等于i时所需的最小代价，则每个轮盘内的积分可以更新集合。由于有的转盘积分为0，则等价于用自己的状态更新自己，使用一维时需要特殊处理，即通过等式左移进行等价替换即可。设p1为0的个数，则有$$f[i]=c+p1/p\ast f[i]+1/p\ast f[i-s1]+1/p\ast f[i-s2]+...+1/p\ast f[i-sm]$$，等价于$$f[i]=c\ast (p-p1)+(f[i-s1]+f[i-s2]+...+f[i-sm])/(p-p1)$$

代码

#include<bits/stdc++.h>

#define x first
#define y second
#define C(i) str[0][i]!=str[1][i]
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
const int N =110,INF=0x3f3f3f3f;
int c[N],p[N];
int s[N][N];
double f[N];

void solve() {
    int n,m;
    cin >>n >>m;
    for(int i=1;i<=n;i++){
        cin >>c[i] >>p[i];
        for(int j=1;j<=p[i];j++)    cin >>s[i][j];
    }

    for(int i=1;i<=m;i++){
        f[i]=1e18;
        for(int j=1;j<=n;j++){
            int p1=0;
            double p2=0;
            for(int k=1;k<=p[j];k++){
                if(!s[j][k])    p1++;
                else p2+=f[max(0,i-s[j][k])];
            }
            f[i]=min(f[i],(p2+p[j]*c[j])/(p[j]-p1));
        }
    }

    printf("%.6lf\n",f[m]);
}


int main() {
    int t = 1;
    //cin >> t;
    while (t--) solve();
    return 0;
}