题目描述

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

思路分析

我读完这道题愣了一会。反应了半天才看懂题。

简单说一下题目，扔1次骰子，则可能的点数，1，2 ,3，4, 5，6。每一种出现的概率就是 1/6。所以当扔骰子数n=1时，应该返回[1/6,1/6,1/6,1/6,1/6,1/6]

当n=2的时候，看下面的表。

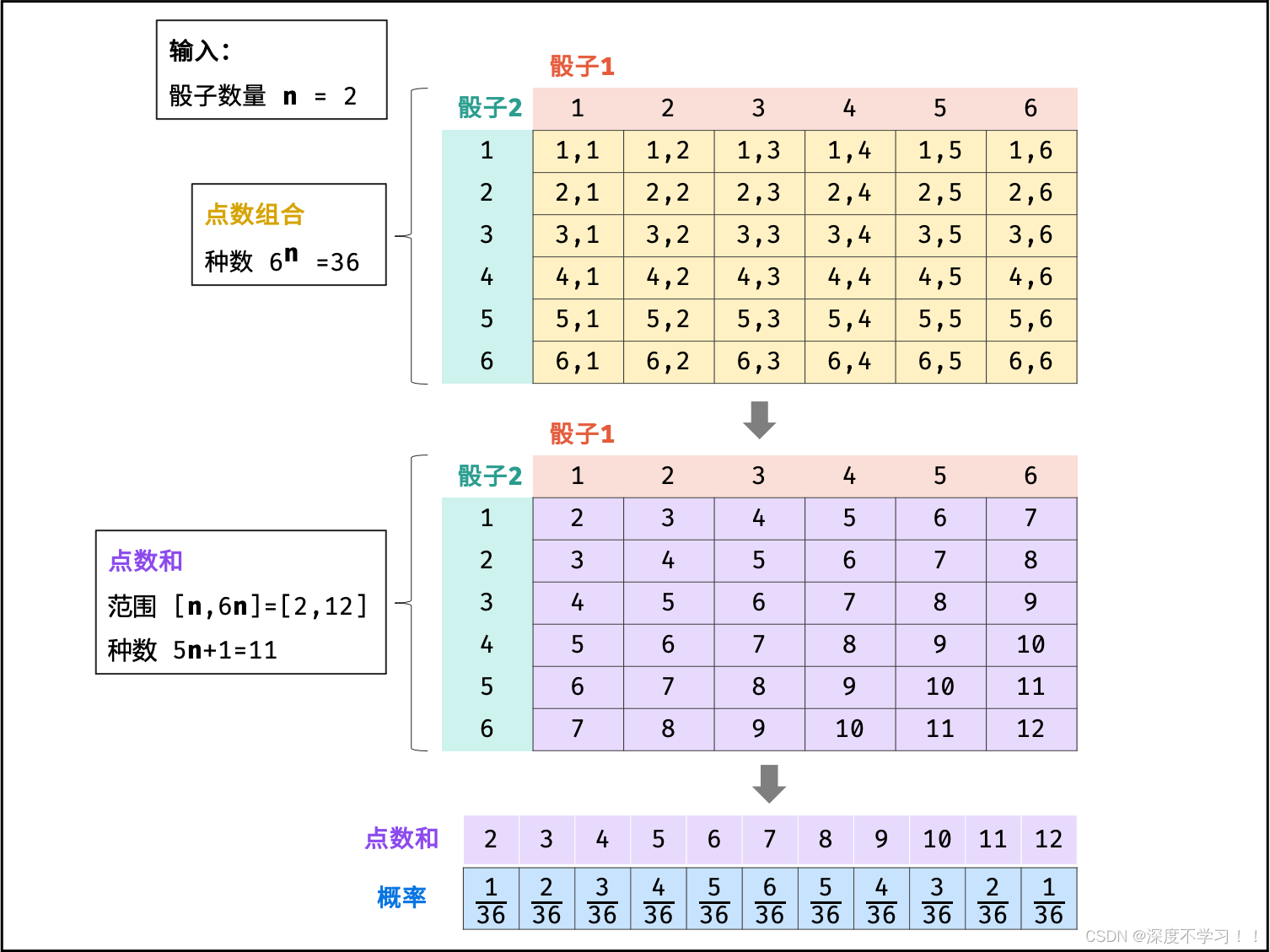
其实就是统计出投骰子的总和点数，计算出这些点数的出现概率:
P (k) =k出现的次数/总次数

总次数好说，因为一共有 n 枚骰子，每枚骰子的点数都有 6 种可能出现的情况。
1次骰子是 6 ，2次骰子是6 * 6。n次就是 6的n次方。

那么现在就是求k出现的总次数了。这里的k可以理解为一个列表，这个列表里存储了n个骰子出现所有数字的和的次数。

使用动态规划来解决，找出这个列表k。

看子问题的递进过程。

当只有一个骰子n=1时候，毫无疑问，总和可能性为[1,2,3,4,5,6]
当n=2的时候，总和可能性为[2,3,4,5,6,7,8,9,10,11,12]

拿其中的总和=3举例：两个骰子出现3，意味着：

• 第一次投1，第二次投2
• 或者第一次投2，第二次投1。

和上一轮的投掷结果相关，显然递推关系就基本出来了。

定义dp[i][j] 表示第i次投，总和为j时，有多少种组合数。

递推公式：dp[i][j] = dp[i-1][j-1]+ dp[i-1][j-2]+ dp[i-1][j-3]… dp[i-1][j-6]

这个式子其实就是先找到上一个状态，就是不加本次骰子的所有点数和，看看那些能凑成本次需要的j，将这些可能性全部相加即可。

        for i in range(2,n+1): # 第i个骰子
            for j in range(i,6*i+1): #j表示点数和，且最大为6*i
                for k in range(1,7): # 相加所有可以组成j的情况
                    if j < k:break  # 显然在递推公式里j>k，做边界处理
                    dp[i][j] +=dp[i-1][j-k]

初始化：
将n=1的情况初始化就行了。
为了方便理解，数组下标为0时的情况作废，数组下标为1就代表n=1 就是第一次投掷的情况。

完整代码

class Solution:
    def dicesProbability(self, n: int) -> List[float]:
        # dp[i][j] 表示投掷第i次，点数和为j，的组合次数有多少个
        num_sum = 6 ** n

        dp = [[0 for _ in range(6*n+1)] for _ in range(n+1)]

        for p in range(1,7):
            dp[1][p] = 1

        for i in range(2,n+1): # 第i个骰子
            for j in range(i,6*i+1): #j表示点数最大为6*i
                for k in range(1,7):
                    if j < k:break
                    dp[i][j] +=dp[i-1][j-k]

        res = []
        for i in range(n,n*6+1):
            res.append(dp[n][i]/num_sum)
        return res
    ```