0. 简介
我们之前经常接触的是使用激光雷达和惯性测量单元(IMU)的互补信息,但是实际使用的过程中IMU如果发生剧烈的颠簸,有可能会导致IMU失效。在广泛使用的迭代最近点(ICP)算法只能为姿态提供约束,而速度只能由IMU预积分进行约束。因此,速度估计倾向于随着姿态结果而更新。最近有一篇博客介绍了将雷达,imu,里程计融合的办法《LIW-OAM: Lidar-Inertial-Wheel Odometry and Mapping》,提出了一种准确而强大的LiDAR惯性轮里程计和地图制图系统,它在基于束调整(BA)的优化框架中融合了来自LiDAR、IMU和轮编码器的测量。轮编码器的参与可以提供速度测量作为一个重要的观测,这有助于LI-OAM提供更准确的状态预测。此外,在优化中通过轮编码器的观测来约束速度变量,可以进一步提高状态估计的准确性。在两个公共数据集上的实验结果表明,我们的系统在绝对轨迹误差(ATE)方面优于所有最先进的LI-OAM系统,并嵌入轮编码器可以大大提高基于BA框架的LI-OAM的性能。目前这个项目已经在Github中开源了
1. 文章贡献
文中我们使用了额外的轮编码器传感器,同时轮编码器传感器的成本要比AHRS低得多。在公共数据集nclt [3]和kaist [7]上的实验结果表明,本文的系统在绝对轨迹误差(ATE)方面优于现有最先进的LI-OAM系统。主要贡献有两个方面:
-
我们提出了一种基于BA的新型LIW-OAM系统,将轮编码器的速度观测嵌入到基于BA的LI优化中。我们的LIW-OAM系统在准确性方面优于大多数最先进的LI-OAM系统。
-
我们已经发布了这项工作的源代码,以促进社区的发展。
2. 预备知识
2.1坐标系
我们用 ( ⋅ ) w (·)^ w (⋅)w 、 ( ⋅ ) l (·)^ l (⋅)l 、 ( ⋅ ) o (·) ^o (⋅)o 和 ( ⋅ ) k (·)^ k (⋅)k 表示在世界坐标系、LiDAR坐标系、IMU坐标系和里程计(即轮编码器)坐标系中的三维点。世界坐标与 ( ⋅ ) l (·) ^l (⋅)l 在起始位置重合。在所有坐标系中,x轴指向前方,y轴指向左侧,z轴指向上方。 我们用 l i l_i li表示在时间 t i t_i ti进行第 i i i次扫描的LiDAR坐标,用 o i o_i oi表示在 t i t_i ti时的对应IMU坐标,然后从LiDAR坐标 l i l_i li到IMU坐标 o i o_i oi的变换矩阵(即外部参数)表示为 T l i o i ∈ S E ( 3 ) T^{o_i}_{l_i} ∈ SE(3) Tlioi∈SE(3):
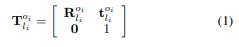
其中,$T^{o_i}{l_i} 由旋转矩阵 由旋转矩阵 由旋转矩阵R^{o_i}{l_i} ∈ SO(3) 和平移向量 和平移向量 和平移向量t^{o_i}{l_i} ∈ \mathbb{R}3$组成。外部参数通常在离线时进行校准,并在在线姿态估计期间保持不变;因此,我们可以简单地使用$To_l$ 表示$T^{o_i}{l_i} 。类似地,从里程表坐标到 I M U 坐标的变换表示为 。类似地,从里程表坐标到IMU坐标的变换表示为 。类似地,从里程表坐标到IMU坐标的变换表示为T^o_k$ ,其中包括 R k o R^o_k Rko 和 t k o t^o_k tko 。
我们使用旋转矩阵R和Hamilton四元数q来表示旋转。在状态向量中,我们主要使用四元数,但旋转矩阵也用于方便地旋转3D向量。 ⊗ ⊗ ⊗表示两个四元数之间的乘法运算。最后,我们用 ( ⋅ ^ ) (\hat{·}) (⋅^)表示某个量的噪声测量或估计。除了姿态,我们还估计速度 v v v、加速度计偏差 b a b_a ba和陀螺仪偏差 b ω b_ω bω,它们都由一个状态向量统一表示:
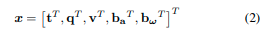
2.2 扫描状态表达式 (需要回顾CT-ICP)
受CT-ICP [5]的启发,我们使用以下方式表示扫描 S S S的状态:
1) S S S开始时间 t b t_b tb的状态(例如 x b x_b xb);
2) S S S结束时间 t e t_e te的状态(例如 x e x_e xe)。
通过这种方式,可以将 [ t b , t e ] [t_b,t_e] [tb,te]期间每个点的状态表示为 x b x_b xb和 x e x_e xe的函数。例如,对于在时间 t p ∈ [ t b , t e ] t_p∈[t_b,t_e] tp∈[tb,te]收集的属于 S S S的点 p p p,可以计算 t p t_p tp时的状态:
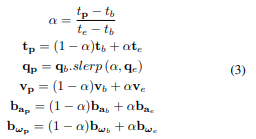
其中,slerp(·)是四元数的球面线性插值运算符。
2.3 IMU-里程计测量模型 (略看)
IMU-里程计包括一个轮式编码器和一个IMU,其中包括一个加速度计和一个陀螺仪。来自IMU的原始陀螺仪和加速度计测量值,即 a ^ t \hat{a}_t a^t和 ω ^ t \hat{ω}_t ω^t,分别为:
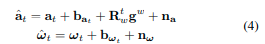
IMU测量值在IMU坐标系中测量,结合了抵消重力和平台动态的力量,并受到加速度计偏差 b a t b_{a_t} bat、陀螺仪偏差 b ω t b_{ω_t} bωt和加性噪声的影响。正如在VINS-Mono [12]中提到的那样,加速度计和陀螺仪测量中的加性噪声被建模为高斯白噪声, n a ∼ N ( 0 , σ a 2 ) , n ω ∼ N ( 0 , σ ω 2 ) n_a∼N(0,σ_a^2),n_ω∼N(0,σ_ω^2) na∼N(0,σa2),nω∼N(0,σω2)。加速度计偏差和陀螺仪偏差被建模为随机游走,其导数为高斯分布, b ˙ a t = n b a ∼ N ( 0 , σ b a 2 ) , b ˙ ω t = n b ω ∼ N ( 0 , σ b ω 2 ) \dot{b}_{a_t}=n_{b_a}∼N(0,σ_{ba}^2),\dot{b}_{ω_t}=n_{b_ω}∼N(0,σ_{b_ω}^2) b˙at=nba∼N(0,σba2),b˙ωt=nbω∼N(0,σbω2)。
轮式编码器根据计数器接收到的脉冲获取轴的旋转速度 τ τ τ,然后根据 τ τ τ和轮子半径计算左后轮和右后轮的速度。
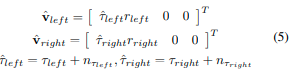
其中, n τ l e f t n_{τ_{left}} nτleft和 n τ r i g h t n_{τ_{right}} nτright是 τ l e f t τ_{left} τleft和 τ r i g h t τ_{right} τright的对应零均值白高斯噪声, v ^ l e f t \hat{v}_{left} v^left和 v ^ r i g h t \hat{v}_{right} v^right是从 τ ^ ⋅ \hat{τ}· τ^⋅和 r ⋅ r· r⋅计算出的两个轮子的测量线性速度。然后,轮式编码器里程计的最终测量模型,在里程计坐标系中测量,可以定义为:
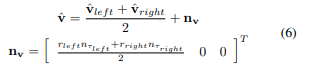
其中, [ n v ] x [n_v]_x [nv]x是两个零均值高斯分布 n v ∼ N ( 0 , σ v 2 ) n_v∼N(0,σ_v^2) nv∼N(0,σv2)的和,仍然是一个零均值高斯分布。
3. 系统概述
图1说明了我们的LIW-OAM框架,它由四个主要模块组成:预处理、初始化、状态估计和点云配准。预处理模块对输入的原始点进行下采样,并以与输入扫描相同的频率预积分IMU-里程计测量。初始化模块估计一些状态参数,包括重力加速度、加速度计偏差、陀螺仪偏差和初始速度。状态估计模块首先将IMU-里程计测量积分到最后状态以预测当前状态,然后执行基于BA的LIW优化以优化当前扫描的状态。最后,点云配准将新点添加到地图中,并删除远离地图的点。
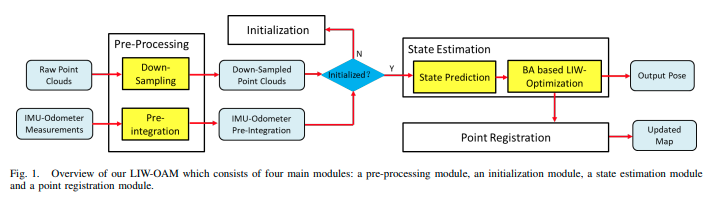
图1. LIW-OAM概述,包括四个主模块:预处理模块、初始化模块、状态估计模块和点注册模块。
4. 预处理(略看)
4.1 下采样
处理大量的3D点会产生高计算成本。为了减少计算复杂度,我们按以下方式对输入点进行下采样。我们将当前输入扫描 S i + 1 S_{i+1} Si+1的点放入一个体积为 0.5 × 0.5 × 0.5 0.5×0.5×0.5 0.5×0.5×0.5(单位:米)的体素中,并使每个体素仅包含一个点,以获得下采样扫描 P i + 1 P_{i+1} Pi+1。这种下采样策略确保了点的密度分布在下采样后在3D空间中是均匀的。
4.2 预积分
通常,IMU-里程计以比LiDAR更高的频率发送数据。预积分两个连续扫描 S i S_i Si和 S i + 1 S_{i+1} Si+1之间的所有IMU-里程计测量可以很好地总结硬件平台从时间 t e i t_{e_i} tei到 t e i + 1 t_{e_{i+1}} tei+1的动态特性,其中 e i e_i ei和 e i + 1 e_{i+1} ei+1分别是 S i S_i Si和 S i + 1 S_{i+1} Si+1的结束时间戳。在这项工作中,我们采用了基于四元数的离散时间IMU-里程计预积分方法[10],并使用[12]中的方法来纳入IMU偏置。具体而言,在相应的IMU坐标 o e i o_{e_i} oei和 o e i + 1 o_{e_{i+1}} oei+1中计算了 S i S_i Si和 S i + 1 S_{i+1} Si+1之间的预积分,即 α ^ e i + 1 e i , η ^ e i + 1 e i , β ^ e i + 1 e i \hat{α}^{e_i}_{e_{i+1}},\hat{η}^{e_i}_{e_{i+1}},\hat{β}^{e_i}_{e_{i+1}} α^ei+1ei,η^ei+1ei,β^ei+1ei和 γ ^ e i + 1 e i \hat{γ}^{e_i}_{e_{i+1}} γ^ei+1ei,其中 α ^ e i + 1 e i , β ^ e i + 1 e i \hat{α}^{e_i}_{e_{i+1}},\hat{β}^{e_i}_{e_{i+1}} α^ei+1ei,β^ei+1ei和 γ ^ e i + 1 e i \hat{γ}^{e_i}_{e_{i+1}} γ^ei+1ei分别是从IMU测量中预积分的平移、速度和旋转,而 η ^ e i + 1 e i \hat{η}^{e_i}_{e_{i+1}} η^ei+1ei是从陀螺仪和轮式编码器里程计测量中预积分的平移。此外,还根据误差状态运动学计算了预积分关于偏置的雅各比矩阵,即 J b a α , J b ω α , J b a β , J b ω β , J b ω γ , J b a η 和 J b ω η J^α_{b_a},J^α_{b_ω},J^β_{b_a},J^β_{b_ω},J^γ_{b_ω},J^η_{b_a}和J^η_{b_ω} Jbaα,Jbωα,Jbaβ,Jbωβ,Jbωγ,Jbaη和Jbωη。
5. 初始化 (需要回顾SR-LIO )
初始化模块旨在估计所有必要的值,包括初始姿态、速度、重力加速度、加速度计偏置和陀螺仪偏置,以进行后续状态估计。与我们先前的工作SR-LIO [19]类似,我们分别为手持设备和车载设备采用运动初始化和静态初始化。有关我们的初始化模块的更多详细信息,请参见[19]。
6. 状态估计
6.1 状态预测
当每个新的下采样扫描 P i + 1 P_{i+1} Pi+1完成时,我们使用IMU-里程计测量来预测 P i + 1 P_{i+1} Pi+1开始时间戳(即 x b i + 1 w x^w_{b_{i+1}} xbi+1w)和结束时间戳(即 x e i + 1 w x^w_{e_{i+1}} xei+1w)的状态,以提供LIW-优化的先验运动。具体而言,预测的状态 x b i + 1 w x^w_{b_{i+1}} xbi+1w(即 t b i + 1 w , R b i + 1 w , v b i + 1 w , b a b i + 1 , b w b i + 1 t^w_{b_{i+1}},R^w_{b_{i+1}},v^w_{b_{i+1}},b_{a_{b_{i+1}}},b_{w_{b_{i+1}}} tbi+1w,Rbi+1w,vbi+1w,babi+1,bwbi+1)被赋值为
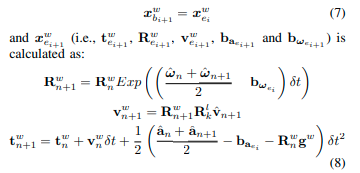
其中 ω ^ ⋅ 、 a ^ ⋅ 和 v ^ ⋅ \hat{ω}·、\hat{a}·和\hat{v}· ω^⋅、a^⋅和v^⋅是来自IMU陀螺仪、IMU加速度计和轮式编码器的测量值, g w g^w gw是世界坐标系下的重力加速度, n n n和 n + 1 n+1 n+1是在 t e i t_{e_i} tei、 t e i + 1 t_{e_{i+1}} tei+1期间获取IMU里程计测量值的两个时间瞬间, δ t δ_t δt是 n n n和 n + 1 n+1 n+1之间的时间间隔。我们迭代地从0增加n到 t e i + 1 − t e i / δ t t_{e_{i+1}} -t_{e_{i}} / δ_t tei+1−tei/δt以获取 x e i + 1 w x^w_{e_{i+1}} xei+1w。当n = 0时, x n w = x e i w x^w_n = x^w_{e_i} xnw=xeiw。 对于 b a e i + 1 b_{a_{e_{i+1}}} baei+1和 b w e i + 1 b_{w_{e_{i+1}}} bwei+1,我们将它们的预测值设为: b a e i + 1 = b a e i , b w e i + 1 = b w e i b_{a_{e_{i+1}}}= b_{a_{e_{i}}},b_{w_{e_{i+1}}} = b_{w_{e_{i}}} baei+1=baei,bwei+1=bwei。
6.2 基于BA的LIW-优化(主要创新)
我们联合利用激光雷达、惯性和轮式编码器的测量值来优化当前扫描 P i + 1 P_{i+1} Pi+1的开始状态(即 x b i + 1 w x^w_{b_{i+1}} xbi+1w)和结束状态(即 x b i + 1 e x^e_{b_{i+1}} xbi+1e),其中变量向量表示为: