参考文献
PINN(Physics-informed Neural Networks)的原理部分可参见https://maziarraissi.github.io/PINNs/
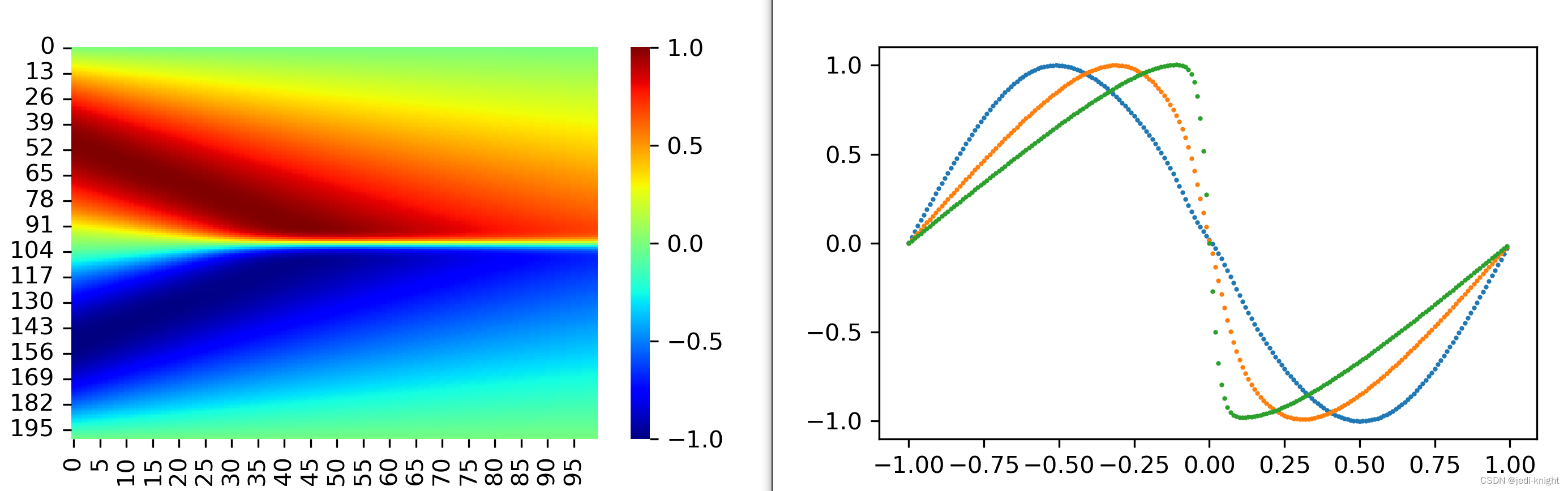
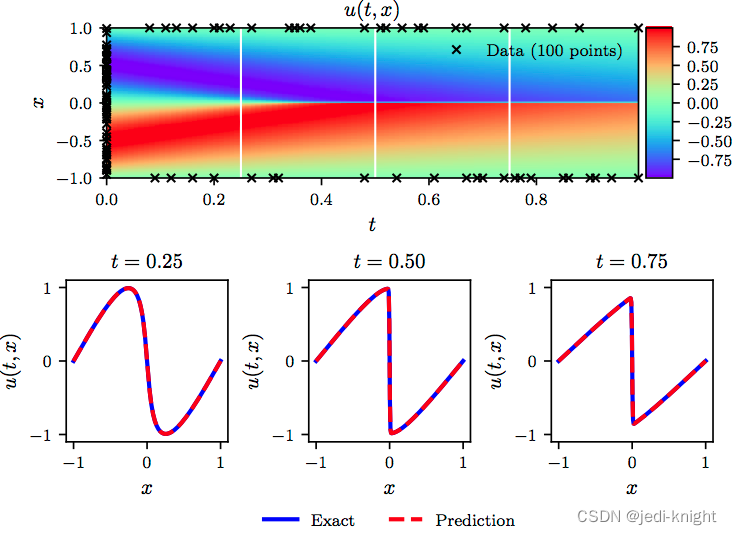
考虑Burgers方程,如下图所示,初始时刻u符合sin分布,随着时间推移在x=0处发生间断.
这是一个经典问题,可使用pytorch通过PINN实现对Burgers方程的求解。
源代码与注释
源代码共含有三个文件,来源于Github https://github.com/jayroxis/PINNs

network.py文件用于定义神经网络的结构
train.py文件用于训练神经网络
evaluate.py文件用于测试训练好的模型绘制结果图
建议使用Anaconda构建运行环境,需要安装pytorch和一些辅助包。
1、network.py 文件
import torch
import torch.nn as nn
from collections import OrderedDict
# 定义神经网络的架构
class Network(nn.Module):
# 构造函数
def __init__(
self,
input_size, # 输入层神经元数
hidden_size, # 隐藏层神经元数
output_size, # 输出层神经元数
depth, # 隐藏层数
act=torch.nn.Tanh, # 输入层和隐藏层的激活函数
):
super(Network, self).__init__()#调用父类的构造函数
# 输入层
layers = [('input', torch.nn.Linear(input_size, hidden_size))]
layers.append(('input_activation', act()))
# 隐藏层
for i in range(depth):
layers.append(
('hidden_%d' % i, torch.nn.Linear(hidden_size, hidden_size))
)
layers.append(('activation_%d' % i, act()))
# 输出层
layers.append(('output', torch.nn.Linear(hidden_size, output_size)))
#将这些层组装为神经网络
self.layers = torch.nn.Sequential(OrderedDict(layers))
# 前向计算方法
def forward(self, x):
return self.layers(x)
2、train.py 文件
import math
import torch
import numpy as np
from network import Network
# 定义一个类,用于实现PINN(Physics-informed Neural Networks)
class PINN:
# 构造函数
def __init__(self):
# 选择使用GPU还是CPU
device = torch.device(
"cuda") if torch.cuda.is_available() else torch.device("cpu")
# 定义神经网络
self.model = Network(
input_size=2, # 输入层神经元数
hidden_size=16, # 隐藏层神经元数
output_size=1, # 输出层神经元数
depth=8, # 隐藏层数
act=torch.nn.Tanh # 输入层和隐藏层的激活函数
).to(device) # 将这个神经网络存储在GPU上(若GPU可用)
self.h = 0.1 # 设置空间步长
self.k = 0.1 # 设置时间步长
x = torch.arange(-1, 1 + self.h, self.h) # 在[-1,1]区间上均匀取值,记为x
t = torch.arange(0, 1 + self.k, self.k) # 在[0,1]区间上均匀取值,记为t
# 将x和t组合,形成时间空间网格,记录在张量X_inside中
self.X_inside = torch.stack(torch.meshgrid(x, t)).reshape(2, -1).T
# 边界处的时空坐标
bc1 = torch.stack(torch.meshgrid(x[0], t)).reshape(2, -1).T # x=-1边界
bc2 = torch.stack(torch.meshgrid(x[-1], t)).reshape(2, -1).T # x=+1边界
ic = torch.stack(torch.meshgrid(x, t[0])).reshape(2, -1).T # t=0边界
self.X_boundary = torch.cat([bc1, bc2, ic]) # 将所有边界处的时空坐标点整合为一个张量
# 边界处的u值
u_bc1 = torch.zeros(len(bc1)) # x=-1边界处采用第一类边界条件u=0
u_bc2 = torch.zeros(len(bc2)) # x=+1边界处采用第一类边界条件u=0
u_ic = -torch.sin(math.pi * ic[:, 0]) # t=0边界处采用第一类边界条件u=-sin(pi*x)
self.U_boundary = torch.cat([u_bc1, u_bc2, u_ic]) # 将所有边界处的u值整合为一个张量
self.U_boundary = self.U_boundary.unsqueeze(1)
# 将数据拷贝到GPU
self.X_inside = self.X_inside.to(device)
self.X_boundary = self.X_boundary.to(device)
self.U_boundary = self.U_boundary.to(device)
self.X_inside.requires_grad = True # 设置:需要计算对X的梯度
# 设置准则函数为MSE,方便后续计算MSE
self.criterion = torch.nn.MSELoss()
# 定义迭代序号,记录调用了多少次loss
self.iter = 1
# 设置lbfgs优化器
self.lbfgs = torch.optim.LBFGS(
self.model.parameters(),
lr=1.0,
max_iter=50000,
max_eval=50000,
history_size=50,
tolerance_grad=1e-7,
tolerance_change=1.0 * np.finfo(float).eps,
line_search_fn="strong_wolfe",
)
# 设置adam优化器
self.adam = torch.optim.Adam(self.model.parameters())
# 损失函数
def loss_func(self):
# 将导数清零
self.adam.zero_grad()
self.lbfgs.zero_grad()
# 第一部分loss: 边界条件不吻合产生的loss
U_pred_boundary = self.model(self.X_boundary) # 使用当前模型计算u在边界处的预测值
loss_boundary = self.criterion(
U_pred_boundary, self.U_boundary) # 计算边界处的MSE
# 第二部分loss:内点非物理产生的loss
U_inside = self.model(self.X_inside) # 使用当前模型计算内点处的预测值
# 使用自动求导方法得到U对X的导数
du_dX = torch.autograd.grad(
inputs=self.X_inside,
outputs=U_inside,
grad_outputs=torch.ones_like(U_inside),
retain_graph=True,
create_graph=True
)[0]
du_dx = du_dX[:, 0] # 提取对第x的导数
du_dt = du_dX[:, 1] # 提取对第t的导数
# 使用自动求导方法得到U对X的二阶导数
du_dxx = torch.autograd.grad(
inputs=self.X_inside,
outputs=du_dX,
grad_outputs=torch.ones_like(du_dX),
retain_graph=True,
create_graph=True
)[0][:, 0]
loss_equation = self.criterion(
du_dt + U_inside.squeeze() * du_dx, 0.01 / math.pi * du_dxx) # 计算物理方程的MSE
# 最终的loss由两项组成
loss = loss_equation + loss_boundary
# loss反向传播,用于给优化器提供梯度信息
loss.backward()
# 每计算100次loss在控制台上输出消息
if self.iter % 100 == 0:
print(self.iter, loss.item())
self.iter = self.iter + 1
return loss
# 训练
def train(self):
self.model.train() # 设置模型为训练模式
# 首先运行5000步Adam优化器
print("采用Adam优化器")
for i in range(5000):
self.adam.step(self.loss_func)
# 然后运行lbfgs优化器
print("采用L-BFGS优化器")
self.lbfgs.step(self.loss_func)
# 实例化PINN
pinn = PINN()
# 开始训练
pinn.train()
# 将模型保存到文件
torch.save(pinn.model, 'model.pth')
运行该文件后模型结果保存在model.pth文件中
3、evaluate.py 文件
import torch
import seaborn as sns
import matplotlib.pyplot as plt
# 选择GPU或CPU
device = torch.device(
"cuda") if torch.cuda.is_available() else torch.device("cpu")
# 从文件加载已经训练完成的模型
model_loaded = torch.load('model.pth', map_location=device)
model_loaded.eval() # 设置模型为evaluation状态
# 生成时空网格
h = 0.01
k = 0.01
x = torch.arange(-1, 1, h)
t = torch.arange(0, 1, k)
X = torch.stack(torch.meshgrid(x, t)).reshape(2, -1).T
X = X.to(device)
# 计算该时空网格对应的预测值
with torch.no_grad():
U_pred = model_loaded(X).reshape(len(x), len(t)).cpu().numpy()
# 绘制计算结果
plt.figure(figsize=(5, 3), dpi=300)
xnumpy = x.numpy()
plt.plot(xnumpy, U_pred[:, 0], 'o', markersize=1)
plt.plot(xnumpy, U_pred[:, 20], 'o', markersize=1)
plt.plot(xnumpy, U_pred[:, 40], 'o', markersize=1)
plt.figure(figsize=(5, 3), dpi=300)
sns.heatmap(U_pred, cmap='jet')
plt.show()
运行该文件后,可绘制u场的结果