SMPL是马普所提出的经典人体模型,目前已成为姿态估计、人体重建等领域必不可少的基础先验。SMPL基于蒙皮和BlendShape实现,从数千个三维人体扫描结果得来,后通过PCA统计学习得来。
论文:SMPL: A Skinned Multi-Person Linear Model
主页:https://smpl.is.tue.mpg.de/index.html
简单来说:SMPL是多个人体模型,这些人体模型的形状、姿态都可以被参数化表示。
SMPL参数一般分为两组:体型参数
β
⃗
\bold{\vec{\beta}}
β和姿态参数
θ
⃗
\bold{\vec{\theta}}
θ。前者决定人体的高矮胖瘦身材比例等,后者决定人体具体姿态。我们从下图即可看出它们的作用:
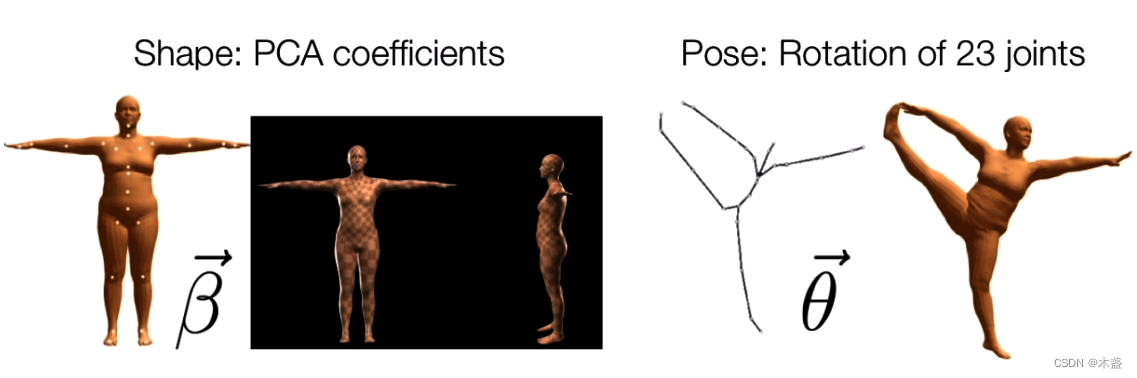
(图片来自链接)
最初始版本(v1.0.0)的SMPL模型有两种性别,对应两个人体模型。每个人体模型有10个体型参数+24x3=72个姿态参数;所以,我们用10+72=82个数就可以表示一个SMPL人体。
随便地,我们生成一组参数:
pose = (np.random.rand((24, 3)) - 0.5) * 0.4 # 24x3=72
beta = (np.random.rand((10,)) - 0.5) * 0.06
这里的pose表示姿态参数
θ
⃗
\bold{\vec{\theta}}
θ,beta表示体型参数
β
⃗
\bold{\vec{\beta}}
β。于是,这一smpl人体可以被生成出来——我们可以用obj文件表示,用MeshLab即可打开:

什么?你问我怎么得到这个obj文件的?
脚本放在下面,按需自取:
import numpy as np
import pickle
class SMPLModel():
def __init__(self, model_path):
"""
SMPL model.
Parameter:
---------
model_path: Path to the SMPL model parameters, pre-processed by
`preprocess.py`.
"""
with open(model_path, 'rb') as f:
params = pickle.load(f)
self.J_regressor = params['J_regressor']
self.weights = params['weights']
self.posedirs = params['posedirs']
self.v_template = params['v_template']
self.shapedirs = params['shapedirs']
self.faces = params['f']
self.kintree_table = params['kintree_table']
id_to_col = {
self.kintree_table[1, i]: i for i in range(self.kintree_table.shape[1])
}
self.parent = {
i: id_to_col[self.kintree_table[0, i]]
for i in range(1, self.kintree_table.shape[1])
}
self.pose_shape = [24, 3]
self.beta_shape = [10]
self.trans_shape = [3]
self.pose = np.zeros(self.pose_shape)
self.beta = np.zeros(self.beta_shape)
self.trans = np.zeros(self.trans_shape)
self.verts = None
self.J = None
self.R = None
self.update()
def set_params(self, pose=None, beta=None, trans=None):
"""
Set pose, shape, and/or translation parameters of SMPL model. Verices of the
model will be updated and returned.
Parameters:
---------
pose: Also known as 'theta', a [24,3] matrix indicating child joint rotation
relative to parent joint. For root joint it's global orientation.
Represented in a axis-angle format.
beta: Parameter for model shape. A vector of shape [10]. Coefficients for
PCA component. Only 10 components were released by MPI.
trans: Global translation of shape [3].
Return:
------
Updated vertices.
"""
if pose is not None:
self.pose = pose
if beta is not None:
self.beta = beta
if trans is not None:
self.trans = trans
self.update()
return self.verts
def update(self):
"""
Called automatically when parameters are updated.
"""
# how beta affect body shape
v_shaped = self.shapedirs.dot(self.beta) + self.v_template
# joints location
self.J = self.J_regressor.dot(v_shaped)
pose_cube = self.pose.reshape((-1, 1, 3))
# rotation matrix for each joint
self.R = self.rodrigues(pose_cube)
I_cube = np.broadcast_to(
np.expand_dims(np.eye(3), axis=0),
(self.R.shape[0]-1, 3, 3)
)
lrotmin = (self.R[1:] - I_cube).ravel()
# how pose affect body shape in zero pose
v_posed = v_shaped + self.posedirs.dot(lrotmin)
# world transformation of each joint
G = np.empty((self.kintree_table.shape[1], 4, 4))
G[0] = self.with_zeros(np.hstack((self.R[0], self.J[0, :].reshape([3, 1]))))
for i in range(1, self.kintree_table.shape[1]):
G[i] = G[self.parent[i]].dot(
self.with_zeros(
np.hstack(
[self.R[i],((self.J[i, :]-self.J[self.parent[i],:]).reshape([3,1]))]
)
)
)
G = G - self.pack(
np.matmul(
G,
np.hstack([self.J, np.zeros([24, 1])]).reshape([24, 4, 1])
)
)
# transformation of each vertex
T = np.tensordot(self.weights, G, axes=[[1], [0]])
rest_shape_h = np.hstack((v_posed, np.ones([v_posed.shape[0], 1])))
v = np.matmul(T, rest_shape_h.reshape([-1, 4, 1])).reshape([-1, 4])[:, :3]
self.verts = v + self.trans.reshape([1, 3])
def rodrigues(self, r):
"""
Rodrigues' rotation formula that turns axis-angle vector into rotation
matrix in a batch-ed manner.
Parameter:
----------
r: Axis-angle rotation vector of shape [batch_size, 1, 3].
Return:
-------
Rotation matrix of shape [batch_size, 3, 3].
"""
theta = np.linalg.norm(r, axis=(1, 2), keepdims=True)
# avoid zero divide
theta = np.maximum(theta, np.finfo(r.dtype).eps)
r_hat = r / theta
cos = np.cos(theta)
z_stick = np.zeros(theta.shape[0])
m = np.dstack([
z_stick, -r_hat[:, 0, 2], r_hat[:, 0, 1],
r_hat[:, 0, 2], z_stick, -r_hat[:, 0, 0],
-r_hat[:, 0, 1], r_hat[:, 0, 0], z_stick]
).reshape([-1, 3, 3])
i_cube = np.broadcast_to(
np.expand_dims(np.eye(3), axis=0),
[theta.shape[0], 3, 3]
)
A = np.transpose(r_hat, axes=[0, 2, 1])
B = r_hat
dot = np.matmul(A, B)
R = cos * i_cube + (1 - cos) * dot + np.sin(theta) * m
return R
def with_zeros(self, x):
"""
Append a [0, 0, 0, 1] vector to a [3, 4] matrix.
Parameter:
---------
x: Matrix to be appended.
Return:
------
Matrix after appending of shape [4,4]
"""
return np.vstack((x, np.array([[0.0, 0.0, 0.0, 1.0]])))
def pack(self, x):
"""
Append zero matrices of shape [4, 3] to vectors of [4, 1] shape in a batched
manner.
Parameter:
----------
x: Matrices to be appended of shape [batch_size, 4, 1]
Return:
------
Matrix of shape [batch_size, 4, 4] after appending.
"""
return np.dstack((np.zeros((x.shape[0], 4, 3)), x))
def save_to_obj(self, path):
"""
Save the SMPL model into .obj file.
Parameter:
---------
path: Path to save.
"""
with open(path, 'w') as fp:
for v in self.verts:
fp.write('v %f %f %f\n' % (v[0], v[1], v[2]))
for f in self.faces + 1:
fp.write('f %d %d %d\n' % (f[0], f[1], f[2]))
if __name__ == '__main__':
smpl = SMPLModel('./model.pkl') # python SMPL model
np.random.seed(9608)
pose = (np.random.rand(*smpl.pose_shape) - 0.5) * 0.4 # (24, 3)
beta = (np.random.rand(*smpl.beta_shape) - 0.5) * 0.06 # (10, )
trans = np.zeros(smpl.trans_shape)
smpl.set_params(beta=beta, pose=pose, trans=trans)
smpl.save_to_obj('./smpl_np.obj')
代码来源:https://github.com/CalciferZh/SMPL