28. 找出字符串中第一个匹配项的下标
首先说明一点,这道力扣题背后所对应的思想就是KMP算法
我们先看看题目:
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
以下是两个示例

1.暴力解法
我们先来讲讲暴力解法的思路,我们可以拿着needle这个串不断的遍历haystack这个字符串,查看是否符合题意,下面我以画图的形式展示思路

可以看到,我们通过对haystack这个字符串进行遍历的同时与needle来进行比较,直到我们查找到了needle字符串
这种思路虽然简单但是时间复杂度很高O(m*n)
那么使用KMP算法就可以让时间复杂度降低了
2.KMP算法
2.1举例
KMP算法的核心思路是利用已经知道的信息来进行重新匹配从而避免从头匹配
例如: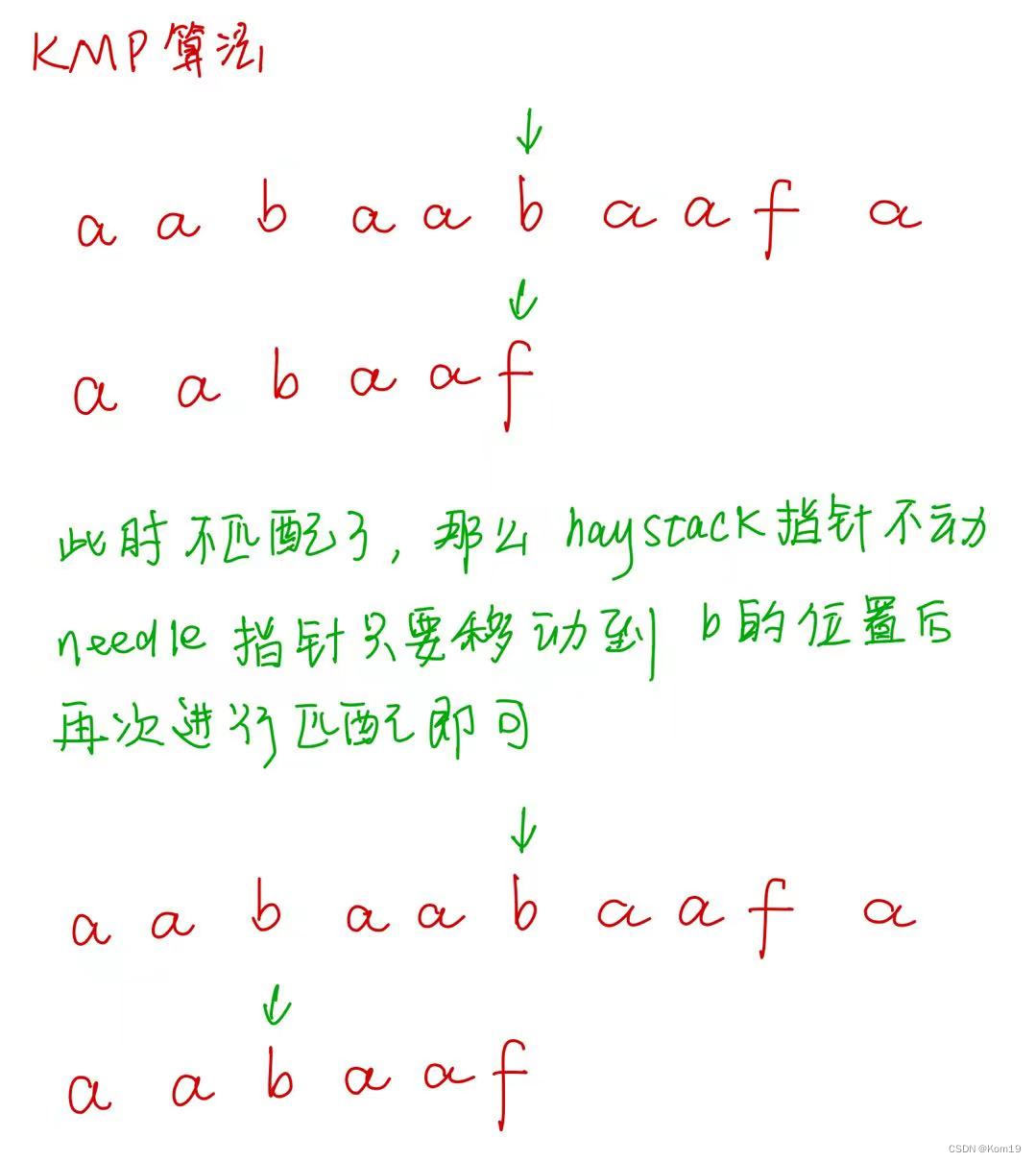
2.2 前缀表
我们根据例子可以发现,当发现不匹配的时候就需要进行回退操作,那么回退到什么位置就成了关键。在这里我们使用前缀表来记录我们每一个元素应该回退的位置应该是哪里。前缀表又是什么呢?前缀表指的是记录i下标之前(以i-1为结尾的下标)的字符串,有多大长度的相等前后缀
在这里前缀指的是:以第一个字母开头,不以最后一个字母结尾的字符串
后缀指的是: 不以第一个字母开头,以最后一个字母结尾的字符串
明确这一点之后
以needle表"aabaaf"为例,前缀有:a,aa,aab,aaba,aabaa 后缀有:f,af,aaf,baaf,abaaf
我们要明确的是当匹配失败的时候要利用已知的信息重新进行匹配,所以说当一个元素进行回退的时候就是要利用已知的信息重新进行匹配。以"aabaaf"举例,当 "f" 这个字母匹配失败以后,我们可以想办法将"f"进行替换重新进行匹配,由于最长相等前后缀是"aa",所以我们可以利用这一点将 "f" 替换成 "b"。所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
2.3 next数组的代码实现
首先可以明确的一点是:next数组就是前缀表
那么用代码的形式来表示出我们的前缀表就很关键了
解决next数组有三种情况:1.初始化 2.前后缀相同 3.前后缀不相同
1.初始化:
next数组使用来记录后退的位置,那么当第一个字母不匹配的时候自然也就没法后退了所以是0
2.前后缀不相同:
用两个指针pre 和 suf 来记录前后缀,当我们发现s.charAt(pre) != s.charAt(suf)时,那么此时就是前后缀不相等的情况了,那么前缀就需要进行回退操作。那么怎么回退呢?
由于我们next数组里面存放的就是前后缀相等的情况,此时只需要回到next[pre - 1]所指向的下标的位置即可,为什么是回到next[pre - 1]所指的下标位置,因为我们前缀表中要求当不匹配的时候就要回下标前一位的位置上
3.前后缀不相同:
我们发现s.charAt(pre) == s.charAt(suf)时,说明此时前后缀相等,由于next数组记录的是前后缀相等的情况,所以此时记录相等前后缀的长度,直接写成 next[pre] = suf 即可
public int[] getNext(String s){
int len = s.length();
int[] next = new int[len];
int pre = 0;
next[0] = 0;
for(int suf = 1;suf < len;suf++){
if(s.charAt(pre) != s.charAt(suf)){
while(pre > 0 && s.charAt(pre) != s.charAt(suf)){
pre = next[pre - 1]
}
}
if(s.charAt(pre) == s.charAt(suf)){
pre++;
}
next[suf] = pre;
}
return next;
}2.4 代码实现KMP数组
当我们的next数组写完以后,我们的KMP算法就完成一大半了
接下来就根据我们上面所提到的思路进行整合就可以完成我们的代码实现了
下面的讲解我就在代码的注释里面完成
class Solution {
public int strStr(String haystack, String needle) {
int[] next = getNext(needle);
int need = 0;//指向子串的指针
for(int hay = 0;hay < haystack.length();hay++){
//当发现不匹配的时候子串的指针进行回退操作
while(need > 0 && haystack.charAt(hay) != needle.charAt(need)){
need = next[need - 1];
}
//当发现匹配的时候子串的指针和主串的指针一起向后移动
if(haystack.charAt(hay) == needle.charAt(need)){
need++;
}
//当走完以后返回主串开始下标即可
if(need == needle.length()){
return hay - needle.length() + 1;
}
}
//当发现走到最后也没有匹配成功此时直接返回-1即可
return -1;
}
public int[] getNext(String needle){
char[] str = needle.toCharArray();
int[] next = new int[str.length];
int prefix = 0;//指向前缀末尾
for(int suffix = 1;suffix < str.length;suffix++){
while(prefix > 0 && str[prefix] != str[suffix]){
prefix = next[prefix - 1];
}
if(str[prefix] == str[suffix]){
prefix++;
}
next[suffix] = prefix;
}
return next;
}
}