学习二叉树必须要了解的各种遍历方式及节点统计

news2024/11/27 22:21:27

  哈喽，大家好，我是小林。今天给大家分享一下对二叉树的一些常规操作。

                           愿我们都能保持一颗向上的心。

目录

  • 一、前序遍历
  • 二、中序遍历
  • 三、后序遍历
  • 四、 统计节点个数
  • 五、统计叶子节点个数
  • 六、第K层的节点个数
  • 七、二叉树的深度
  • 八、查找值为x的节点
  • 九、层序遍历
  • 十、判断是否是完全二叉树

一、前序遍历


//前序遍历
void PreOrder(BTNode* root)
{
	//如果根为NULL，直接返回
	if (root == NULL)
	{
		//printf("NULL "); //可打印可不打印
		return;
	}
	//前序遍历，先打印根
	printf("%c ", root->val);
	//遍历左孩子
	PreOrder(root->left);
	//遍历右孩子
	PreOrder(root->right);
}

二、中序遍历

//中序遍历
void InOrder(BTNode* BT)
{
	if (BT == NULL)
	{
		//printf("NULL "); //可打印可不打印
		return;
	}
	//先遍历左孩子
	InOrder(BT->left);
	//打印根
	printf("%c ", BT->val);
	//遍历右孩子
	InOrder(BT->right);
}

三、后序遍历

//后序遍历
void PostOrder(BTNode* BT)
{
	if (BT == NULL)
	{
		//printf("NULL "); //可打印可不打印
		return;
	}
	//先遍历左孩子
	PostOrder(BT->left);
	//再遍历右孩子
	PostOrder(BT->right);
	//打印根
	printf("%c ", BT->val);

}

四、 统计节点个数


//统计个数
size_t BinaryTreeSize(BTNode* BT)
{
	//如果BT是NULL，则说明不是节点，所以返回0,节点就+1
	return BT == NULL ? 0 : 1 + BinaryTreeSize(BT->left) + BinaryTreeSize(BT->right);
}

五、统计叶子节点个数

//统计叶子个数
size_t BinaryLeafSize(BTNode* root)
{
	//根为空，返回0
	if (root == NULL)
		return 0;

	//左孩子和右孩子都为空，是叶子节点，返回1
	if (root->left == NULL && root->right == NULL)
		return 1;

	//递归遍历
	return BinaryLeafSize(root->left) + 
		   BinaryLeafSize(root->right);

}

六、第K层的节点个数

//第K层的节点个数
size_t BinaryLevelKSize(BTNode* root, int k)
{
	//根为空，返回0
	if (root == NULL)
		return 0;

	//如果k等于1，说明在第k层,返回1
	if (k == 1)
		return 1;

	return BinaryLevelKSize(root->left, k - 1) +   
	       BinaryLevelKSize(root->right, k - 1);
}

七、二叉树的深度

//二叉树的深度
int BinaryTreeDepth(BTNode* root)
{
	//根为空，返回0
	if (root == NULL)
		return 0;

	//接收左孩子的深度
	int leftRet = BinaryTreeDepth(root->left);
	//接收右孩子深度
	int rightRet = BinaryTreeDepth(root->right);

	//返回左右孩子较大的那一个
	return leftRet < rightRet ? rightRet + 1 : leftRet + 1;

}

八、查找值为x的节点

//查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	//根为空，返回NULL
	if (root == NULL)
		return NULL;
	
	//root的值等于val，返回root
	if (root->val == x)
		return root;

	//遍历左孩子找x
	BTNode* left = BinaryTreeFind(root->left, x);
	//如果值等于x，返回当前节点
	if (left->val == x)
		return left;

	//遍历右孩子找x
	BTNode* right = BinaryTreeFind(root->right, x);
	//如果值等于x，返回当前节点
	if (right->val == x)
		return right;

	//左右孩子都没找到，返回null
	return NULL;
}

九、层序遍历

  层序遍历需要用到队列，如果不知道队列的朋友可以看看我分享的这篇文章队列的实现，队列的实现链接git链接。只需要把.h和.c文件拿过来用并修改一下队列存放的数据类型即可使用。


//层序遍历
void LevelOrder(BTNode* root)
{
	//如果root为空，返回
	if (root == NULL)
		return;

	//创建一个队列
	Queue q;
	//初始化队列
	QueueInto(&q);

	//根节点入队
	QueuePush(&q, root);

	//循环入队出队
	while (!QueueIsEmpty(&q))
	{
		//保存队头节点
		BTNode* Front = QueueGetFront(&q);
		//队头节点，也就是根节点出队
		QueuePop(&q);

		//俩个孩子入队,但确保该节点不能为空
		if (Front != NULL)
		{
			//打印
			printf("%c ", Front->val);
			//俩孩子入队
			QueuePush(&q, Front->left);
			QueuePush(&q, Front->right);

		}
		else
			printf("NULL "); //可要可不要
	}
	printf("\n");

}

十、判断是否是完全二叉树

先给大家看看完全二叉树和非完全二叉树的区别。

非完全二叉树
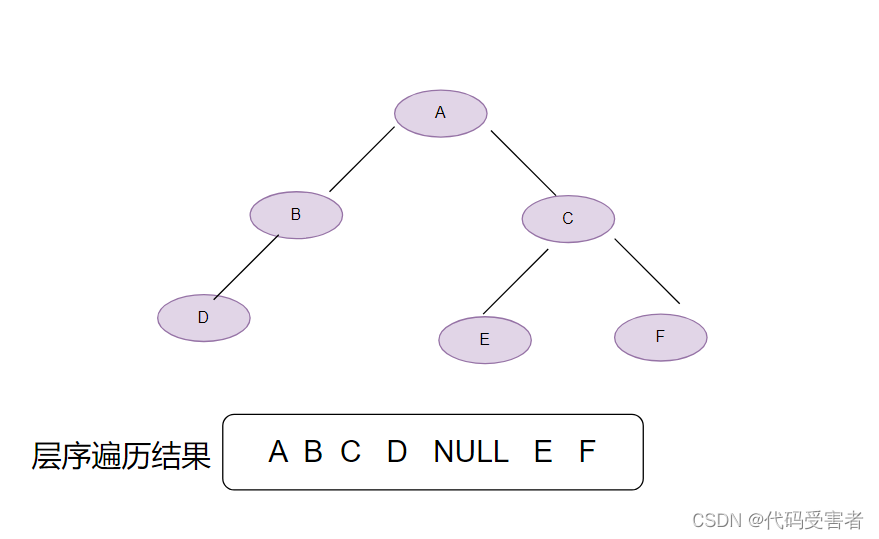
在这里插入图片描述

层序遍历结果是: A B C D NULL E F

完全二叉树
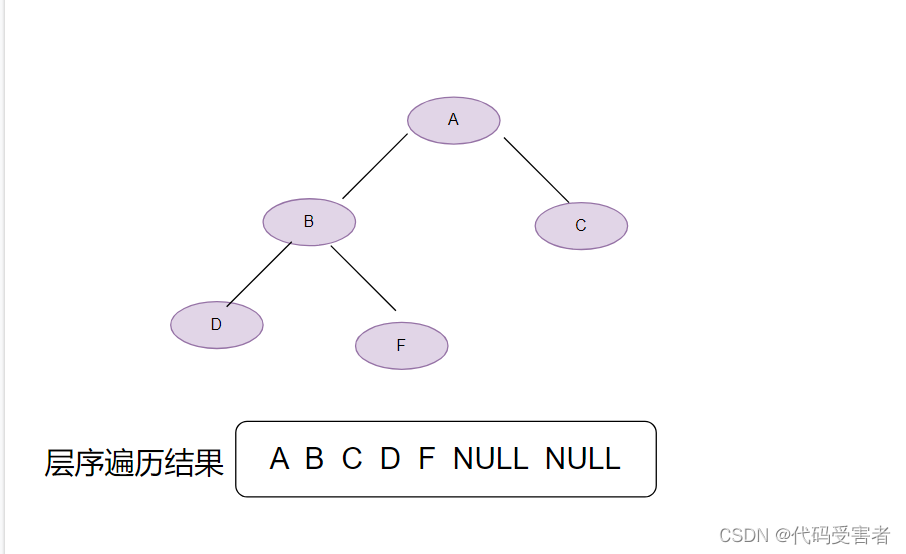
在这里插入图片描述
层序遍历结果 : A B C D F NULL NULL

结论: 完全二叉树层序遍历在遇到NULL后，后面将会是连续的NULL，如果在出现NULL之后还遇到非NULL的值，那么说明这不是一个完全二叉树。

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;


	//创建一个队列
	Queue q;
	//初始化队列
	QueueInto(&q);
	//根入队
	QueuePush(&q, root);
	while (!QueueIsEmpty(&q))
	{
		BTNode* Front = QueueGetFront(&q);
		QueuePop(&q);
		//如果队头是NULL，那么说明到了最后的后一个节点
		if (Front == NULL)
			break;

		//Front不为空，2个孩子入队
		QueuePush(&q, Front->left);
		QueuePush(&q, Front->right);
	}

	while (!QueueIsEmpty(&q))
	{
		//继续以上操作，不过接下来的Front必须全为空，否则就不是完全二叉树
		BTNode* Front = QueueGetFront(&q);
		QueuePop(&q);

		if (Front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	//循环结束说明后面都是NULL，所以是完全二叉树
	QueueDestroy(&q);
	return true;
}

全部代码

#define _CRT_SECURE_NO_WARNINGS 1

#include "Queue.h"

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType val;

}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* Node = (BTNode*)malloc(sizeof(BTNode));
	if(Node == NULL)
	{
		printf("malloc fail\n");
	}

	Node->val = x;
	Node->left = Node->right = NULL;

	return Node;
}


BTNode* BinaryCreate()
{
	BTNode* BTNodeA = BuyNode('A');
	BTNode* BTNodeB = BuyNode('B');
	BTNode* BTNodeC = BuyNode('C');
	BTNode* BTNodeD = BuyNode('D');
	BTNode* BTNodeE = BuyNode('E');
	BTNode* BTNodeF = BuyNode('F');
	//BTNode* BTNodeG = BuyNode('G');


	BTNodeA->left = BTNodeB;
	BTNodeA->right = BTNodeC;
	BTNodeB->left = BTNodeD;
	//链上G那么就是完全二叉树了，不链上则不是
	//BTNodeB->right = BTNodeG;
	BTNodeC->left = BTNodeE;
	BTNodeC->right = BTNodeF;

	return BTNodeA;
}

//前序遍历
void PreOrder(BTNode* root)
{
	//如果根为NULL，直接返回
	if (root == NULL)
		return;

	//前序遍历，先打印根
	printf("%c ", root->val);
	//遍历左孩子
	PreOrder(root->left);
	//遍历右孩子
	PreOrder(root->right);
}

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%c ", root->val);
	InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->val);

}

//统计节点个数
size_t BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

//统计叶子个数
size_t BinaryLeafSize(BTNode* root)
{
	//根为空，返回0
	if (root == NULL)
		return 0;

	//左孩子和右孩子都为空，是叶子节点，返回1
	if (root->left == NULL && root->right == NULL)
		return 1;

	//递归遍历
	return BinaryLeafSize(root->left) + BinaryLeafSize(root->right);

}

//第K层的节点个数
size_t BinaryLevelKSize(BTNode* root, int k)
{
	//根为空，返回0
	if (root == NULL)
		return 0;

	//如果k等于1，说明在第k层,返回1
	if (k == 1)
		return 1;

	return BinaryLevelKSize(root->left, k - 1) + BinaryLevelKSize(root->right, k - 1);
}

//二叉树的深度
int BinaryTreeDepth(BTNode* root)
{
	//根为空，返回0
	if (root == NULL)
		return 0;

	//接收左孩子的深度
	int leftRet = BinaryTreeDepth(root->left);
	//接收右孩子深度
	int rightRet = BinaryTreeDepth(root->right);

	//返回左右孩子较大的那一个
	return leftRet < rightRet ? rightRet + 1 : leftRet + 1;

}

//查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	//根为空，返回NULL
	if (root == NULL)
		return NULL;
	
	//root的值等于val，返回root
	if (root->val == x)
		return root;

	//遍历左孩子找x
	BTNode* left = BinaryTreeFind(root->left, x);
	//如果值等于x，返回当前节点
	if (left->val == x)
		return left;

	//遍历右孩子找x
	BTNode* right = BinaryTreeFind(root->right, x);
	//如果值等于x，返回当前节点
	if (right->val == x)
		return right;

	//左右孩子都没找到，返回null
	return NULL;
}

//层序遍历
void LevelOrder(BTNode* root)
{
	//如果root为空，返回
	if (root == NULL)
		return;

	//创建一个队列
	Queue q;
	//初始化队列
	QueueInto(&q);

	//根节点入队
	QueuePush(&q, root);

	//循环入队出队
	while (!QueueIsEmpty(&q))
	{
		//保存队头节点
		BTNode* Front = QueueGetFront(&q);
		//队头节点，也就是根节点出队
		QueuePop(&q);

		//俩个孩子入队,但确保该节点不能为空
		if (Front != NULL)
		{
			//打印
			printf("%c ", Front->val);
			//俩孩子入队
			QueuePush(&q, Front->left);
			QueuePush(&q, Front->right);

		}
		else
			printf("NULL "); //可要可不要
	}
	printf("\n");

}

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;


	//创建一个队列
	Queue q;
	//初始化队列
	QueueInto(&q);
	//根入队
	QueuePush(&q, root);
	while (!QueueIsEmpty(&q))
	{
		BTNode* Front = QueueGetFront(&q);
		QueuePop(&q);
		//如果队头是NULL，那么说明到了最后的后一个节点
		if (Front == NULL)
			break;

		//Front不为空，2个孩子入队
		QueuePush(&q, Front->left);
		QueuePush(&q, Front->right);
	}

	while (!QueueIsEmpty(&q))
	{
		//继续以上操作，不过接下来的Front必须全为空，否则就不是完全二叉树
		BTNode* Front = QueueGetFront(&q);
		QueuePop(&q);

		if (Front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	//循环结束说明后面都是NULL，所以是完全二叉树
	QueueDestroy(&q);
	return true;
}


int main()
{
	BTNode* root = BinaryCreate();
	printf("前序遍历:");
	PreOrder(root);
	printf("\n");

	printf("中序遍历:");
	InOrder(root);
	printf("\n");

	printf("后序遍历:");
	PostOrder(root);
	printf("\n");

	printf("树的总节点个数:");
	printf("%d",BinaryTreeSize(root));
	printf("\n");

	printf("树的叶子节点个数");
	printf("%d", BinaryLeafSize(root));
	printf("\n");

	printf("找到的节点值为：");
	BTNode* BT = BinaryTreeFind(root,'B');
	printf("%c ",BT->val);
	printf("\n");

	printf("树的深度是：");
	printf("%d ", BinaryTreeDepth(root)); 
	printf("\n");

	int i = 3;
	printf("树的第%d层的节点数:",i);
	printf("%d ", BinaryLevelKSize(root,i));
	printf("\n");

	printf("层序遍历:");
	LevelOrder(root);

	bool a = BinaryTreeComplete(root);
	if (a)
		printf("是完全二叉树\n");
	else
		printf("不是完全二叉树\n");

}

队列的代码 Queue.c

#include "Queue.h"

//初始化
void QueueInto(Queue* q)
{
	assert(q);
	q->head = NULL;
	q->tail = NULL;
}

//创建节点
QueueNode* CreateNode(QDataType x)
{
	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newNode == NULL)
	{
		printf("malloc faile\n");
		exit(-1);
	}
	newNode->next = NULL;
	newNode->val = x;
	return newNode;
}

//数据入队
void QueuePush(Queue* q, QDataType x)
{
	//断言
	assert(q);

	//创建节点
	QueueNode* newNode = CreateNode(x);
	//如果head NULL
	if (q->head == NULL)
	{
		q->head = newNode;
		q->tail = newNode;
	}
	else
	{
		//尾节点指向新节点
		q->tail->next = newNode;
		//尾节点移动位置
		q->tail = newNode;
	}
}

//判断队列是否为空
bool QueueIsEmpty(Queue* q)
{
	return q->head == NULL;
}

//数据出队
void QueuePop(Queue* q)
{
	assert(q);
	//要保证队列里有数据可以删除
	assert(!QueueIsEmpty(q));

	//头删
	QueueNode* next = q->head->next;
	free(q->head);
	q->head = next;
}

//获取队头
QDataType QueueGetFront(Queue* q)
{
	assert(q);
	//要保证队列里有数据
	assert(!QueueIsEmpty(q));
	return q->head->val;
}

//获取队尾
QDataType QueueGetBack(Queue* q)
{
	assert(q);
	//要保证队列里有数据
	assert(!QueueIsEmpty(q));
	return q->tail->val;
}


//获取队列长度
size_t QueueGetSize(Queue* q)
{
	assert(q);
	//要保证队列里有数据
	assert(!QueueIsEmpty(q));
	int len = 1;
	QueueNode* head = q->head;
	QueueNode* tail = q -> tail;
	while (head != tail)
	{
		len++;
		head = head->next;
	}
	return len;
}

//销毁
void QueueDestroy(Queue* q)
{
	QueueNode* cru = q->head;
	while (cru != NULL)
	{
		//存储下一个位置地址
		QueueNode* next = cru->next;
		free(cru);
		cru = next;
	}
	
}

Queue.h的代码

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;

//队列的节点
typedef struct QueueNode
{
	QDataType val;
	struct QueueNode* next;
}QueueNode;


//队列
typedef struct Queue
{
	//一个指针指向头
	QueueNode* head;
	//一个指针指向尾
	QueueNode* tail;
}Queue;

//队列初始化
void QueueInto(Queue* q);

//数据入队
void QueuePush(Queue* q,QDataType x);

//判断队列是否为空
bool QueueIsEmpty(Queue* q);

//数据出队
void QueuePop(Queue* q);

//获取队头
QDataType QueueGetFront(Queue* q);

//获取队尾
QDataType QueueGetBack(Queue* q);


//获取队列长度
size_t QueueGetSize(Queue* q);


//销毁
void QueueDestroy(Queue* q);

  感谢大家支持，如果不嫌弃，给个关注呗。谢谢大佬们了。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/88417.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

TensorFlow TFRecords简介

TensorFlow TFRecords简介

TensorFlow TFRecords简介 这篇博客将介绍TensorFlow的TFRecords&#xff0c;提供有关TFRecords的所有信息的一应俱全的介绍。从如何构建基本TFRecords到用于训练 SRGAN 和 ESRGAN 模型的高级TFRecords的所有内容。包括什么是TFRecords&#xff0c;如何序列化&#xff0c;反序…
阅读更多...
SQL 语句练习03

SQL 语句练习03

目录 一、建表 二、插入数据 三、查询 一、建表 这里先建好我们下面查询需要的表&#xff0c;方便后续查询。 建立如下学生表(命名格式“姓名拼音_三位学号_week5s”&#xff0c; 如LBJ_023_week5s&#xff09;create table LYL_116_week5s(SNO varchar(4) primary key,SNA…
阅读更多...
【Kubernetes】DashBoard部署

【Kubernetes】DashBoard部署

kubernetes&#xff0c;是一个全新的基于容器技术的分布式架构领先方案&#xff0c;是谷歌严格保密十几年的秘密武器----Borg系统的一个开源版本&#xff0c;于2014年9月发布第一个版本&#xff0c;2015年7月发布第一个正式版本。 kubernetes的本质是一组服务器集群&#xff0…
阅读更多...
数字孪生智慧水务建设综述

数字孪生智慧水务建设综述

随着新时期治水方针的逐步落实&#xff0c;水利现代化、智能化建设已全面开启&#xff0c;数字孪生等新技术的成熟&#xff0c;也为智慧水务体系的搭建提供了技术保障&#xff0c;新时代治水新思路正逐步得到落实。本文将重点对智慧水务的内涵及建设内容进行解读&#xff0c;力…
阅读更多...
2022年航空与物流行业研究报告

2022年航空与物流行业研究报告

第一章 行业概况 航空与物流行业是指以各种航空飞行器为运输工具&#xff0c;以空中运输的方式运载人员或货物的企业。航空公司是以各种航空飞行器为运输工具为乘客和货物提供民用航空服务的企业。航空公司使用的飞行器可以是他们自己拥有的&#xff0c;也可以是租来的&#x…
阅读更多...
物联网通信技术原理-作业汇总（更新ing）

物联网通信技术原理-作业汇总（更新ing）

第一章 第二章 第三章 第四章 第五章 1. 移动通信中典型的多址接入方式有哪些&#xff1f;简要说明其工作原理2. 分集技术的基本原理是什么&#xff1f;简要说明空间、频率和时间分集、合并的异同。 1&#xff09;分集技术的基本原理 通过多个信道&#xff08;时间、频率或…
阅读更多...
25.访客功能

25.访客功能

访客功能 一、需求分析 用户在浏览我的主页时&#xff0c;需要记录访客数据&#xff0c;访客在一天内每个用户只记录一次。 首页展示最新5条访客记录 我的模块&#xff0c;分页展示所有的访客记录 二、数据库表 visitors&#xff08;访客记录表&#xff09; { “_id”: …
阅读更多...
尚医通 (三十五) --------- 预约下单

尚医通 (三十五) --------- 预约下单

目录一、预约下单前端1. 封装 api 请求2. 页面修改二、后端逻辑1. 需求分析2. 搭建 service-order 模块3. 添加订单基础类4. 封装 Feign 调用获取就诊人接口5. 封装 Feign 调用获取排班下单信息接口6. 实现下单接口7. 预约成功后处理逻辑① rabbit-util 模块封装② 封装短信接口…
阅读更多...
C++ Reference: Standard C++ Library reference: Containers: map: map: cend

C++ Reference: Standard C++ Library reference: Containers: map: map: cend

C官网参考链接&#xff1a;https://cplusplus.com/reference/map/map/cend/ 公有成员函数 <map> std::map::cend const_iterator cend() const noexcept;返回指向结束的const_iterator 返回一个指向容器结束后元素的const_iterator。 const_iterator是指向const内容的it…
阅读更多...
正弦交流电物理量表征

正弦交流电物理量表征

前言 这一讲主要来表征正弦交流电的物理量 文章目录前言一、周期和频率二、最大值、有效值和平均值一、周期和频率 周期&#xff1a;正弦交流电每重复变化1次所需要的时间称为周期&#xff0c;用符号T表示&#xff0c;单位是秒&#xff08;s&#xff09;。 频率&#xff1a;正…
阅读更多...
web前端期末大作业 绿色环境保护(4个页面) HTML5网站模板农业展示网站 html5网页制作代码 html5网页设计作业代码 html制作网页案例代码

web前端期末大作业 绿色环境保护(4个页面) HTML5网站模板农业展示网站 html5网页制作代码 html5网页设计作业代码 html制作网页案例代码

&#x1f380; 精彩专栏推荐&#x1f447;&#x1f3fb;&#x1f447;&#x1f3fb;&#x1f447;&#x1f3fb; ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 &#x1f482; 作者主页: 【主页——&#x1f680;获取更多优质源码】 &#x1f393; web前端期末大作业…
阅读更多...
体育馆场地预约管理系统/球馆管理系统

体育馆场地预约管理系统/球馆管理系统

摘 要 随着体育馆规模的不断扩大&#xff0c;人流数量的急剧增加&#xff0c;有关体育馆的各种信息量也在不断成倍增长。面对庞大的信息量&#xff0c;就需要有体育馆场地预约管理系统来提高体育馆工作的效率。通过这样的系统&#xff0c;我们可以做到信息的规范管理和快速查询…
阅读更多...
TCP/IP网络原理 【IP篇】

TCP/IP网络原理 【IP篇】

&#x1f389;&#x1f389;&#x1f389;写在前面&#xff1a; 博主主页&#xff1a;&#x1f339;&#x1f339;&#x1f339;戳一戳&#xff0c;欢迎大佬指点&#xff01; 目标梦想&#xff1a;进大厂&#xff0c;立志成为一个牛掰的Java程序猿&#xff0c;虽然现在还是一个…
阅读更多...
聚观早报 | 马斯克丢掉世界首富宝座；加密货币FTX创始人被捕

聚观早报 | 马斯克丢掉世界首富宝座；加密货币FTX创始人被捕

今日要闻&#xff1a;马斯克丢掉世界首富宝座&#xff1b;加密货币FTX创始人被捕&#xff1b;美团推出高峰打车极速版&#xff1b;魔兽制作组正研发新功能&#xff1b;SpaceX出售公司内部股票马斯克丢掉世界首富宝座 12 月 13 日消息&#xff0c;据国外媒体报道&#xff0c;受特…
阅读更多...
7-54 孤岛营救问题——状压bfs+三维标记

7-54 孤岛营救问题——状压bfs+三维标记

1944 年&#xff0c;特种兵麦克接到国防部的命令&#xff0c;要求立即赶赴太平洋上的一个孤岛&#xff0c;营救被敌军俘虏的大兵瑞恩。瑞恩被关押在一个迷宫里&#xff0c;迷宫地形复杂&#xff0c;但幸好麦克得到了迷宫的地形图。迷宫的外形是一个长方形&#xff0c; 其南北方…
阅读更多...
二、小程序框架

二、小程序框架

目录 框架 一、响应的数据绑定 二、页面管理 三、基础组件 四、丰富的API 模块化 一、模块化 二、文件作用域 三、API 视图层 View 一、WXML 事件 什么是事件 事件的使用方式 使用 WXS 函数响应事件 事件详解 框架 小程序开发框架的目标是通过尽可能简单、高效…
阅读更多...
万字长文详解 YOLOv1-v5 系列模型

万字长文详解 YOLOv1-v5 系列模型

一&#xff0c;YOLOv1二&#xff0c;YOLOv2三&#xff0c;YOLOv3四&#xff0c;YOLOv4五&#xff0c;YOLOv5参考资料 一&#xff0c;YOLOv1 YOLOv1 出自 2016 CVPR 论文 You Only Look Once:Unified, Real-Time Object Detection. YOLO 系列算法的核心思想是将输入的图像经过…
阅读更多...
同时安装python3和Python2

同时安装python3和Python2

一刚开始我很疑惑&#xff0c;Python为何要并行两个版本呢&#xff1f;今天我算知道了&#xff0c;原来是因为有的项目一直在用python2。虽然我已经安装了python3但是那些使用python2进行部署的项目我仍然无法使用&#xff0c;这就导致我要在电脑上同时安装python2和Python3了。…
阅读更多...
【无标题】SIP网络广播音频模块

【无标题】SIP网络广播音频模块

SIP2101V和SIP2103V网络音频模块是一款通用的独立SIP音频功能模块&#xff0c;可以轻松地嵌入到OEM产品中。该模块对来自网络的SIP协议及RTP音频流进行编解码。 该模块支持多种网络协议和音频编解码协议&#xff0c;可用于VoIP和IP寻呼以及高质量音乐流媒体播放等应用。同时&a…
阅读更多...
如何将onnx转ncnn供移动端推理使用

如何将onnx转ncnn供移动端推理使用

ncnn是一个为手机端极致优化的高性能神经网络前向计算框架。基于 ncnn&#xff0c;开发者能够将深度学习算法轻松移植到手机端高效执行&#xff0c;开发出人工智能 APP&#xff0c;将 AI 带到你的指尖。 但是onnx直接转ncnn会存在很多问题&#xff0c;所以一般考虑都是先将onn…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023