目录
前言
1.浮点型
2.字符型
3.易错点
4.思维导图
前言
我们学习了C语言中用来表示整数的数据类型:整型(int),今天我们会学习用来表示小数的数据类型:浮点型(float)
1.浮点型
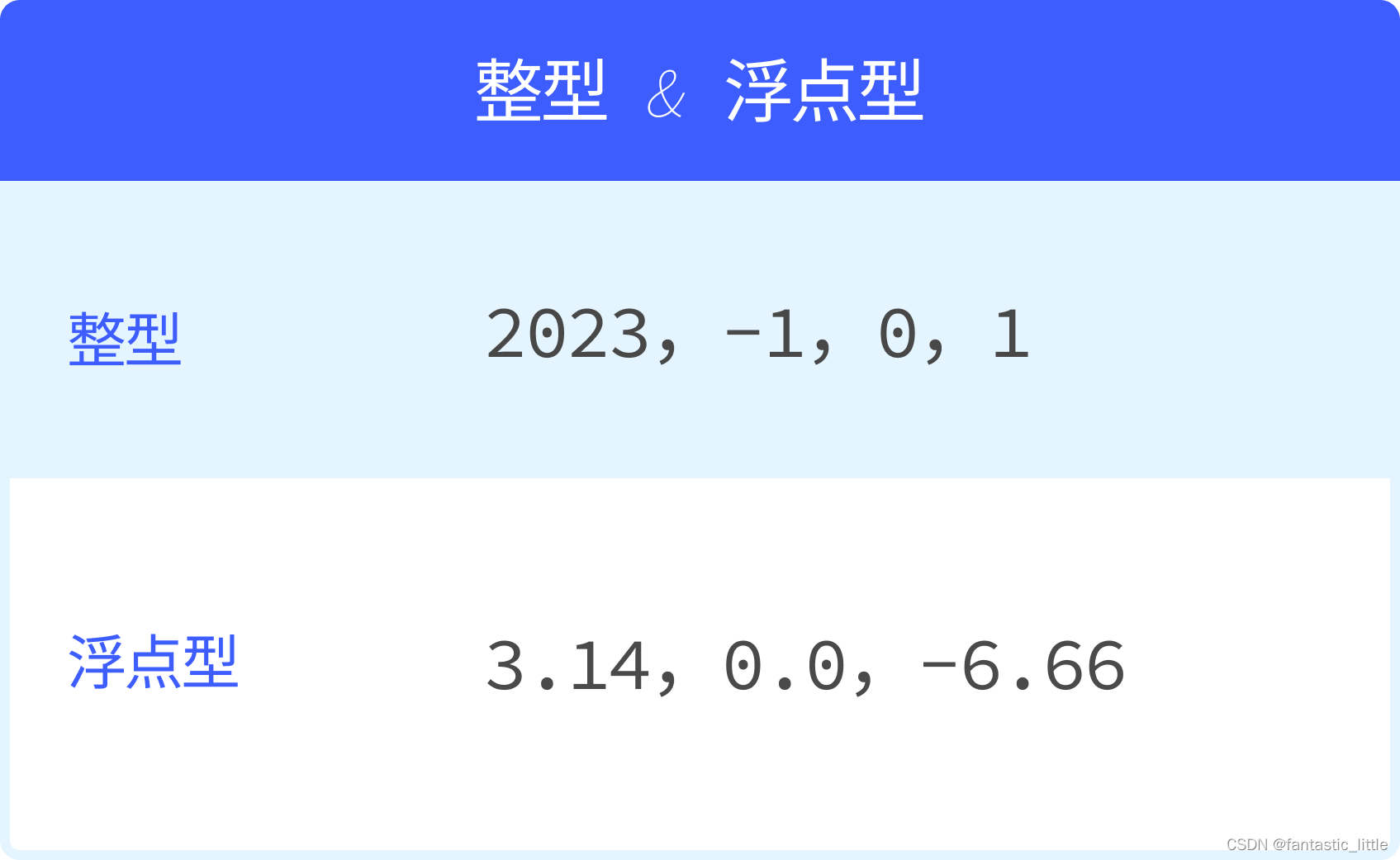
1.1—下面一些小数,在C语言里,我们把它们叫做浮点数(float)
3.1415
0.00
-6.6
1.一个正小数3.1415
2.写成小数格式的0,0.0
3.一个负小数-6.66

1.2—为什么好好的小数不叫小数,要教浮点数呢,这是因为在C语言和计算机中存储小数的底层机制决定了的。为了方便记忆,可以简单粗糙的记忆为:因为小数有小数点,所以叫浮点数😄。

更详细一点解释的话。计算机对于小数的存储分为两部分,一部分是数字本身,一部分是小数点所在的位置。
比如3.1415和314.15这两个数字,计算机C语言存储这两个数字的时候,都会存储31415这个数字,同时,对于第一个数,小数点会记录在3的后面;对于第二个数,小数点会记录在314的后面。
因此这个小数点是“浮动的”,所以就叫浮点数了。
1.3-同样的,我们可以使用printf()语句来打印一个小数
printf("一个小数%f",3.14);
1.printf()指令
2.printf()的语法格式,括号
3.要打印输出的字符串
4.%f,小数的”替代符号“
5.3.1415要输出的小数
6.两个语法的固定符号
1.4-同样的,我们还可以输出一个2.22;
printf("%f",2.22);
输出结果
2.220000
以及输出一个0.0:
printf("%f",0.0);
输出结果
0.000000
1.5—在格式化的输出里面,整型使用的是%d,浮点型使用的是%f,聪明的你可能猜到了,这是因为f是浮点英文float的首字母。
定义整型变量的时候我们使用int,定义浮点型变量的时候我们使用float
float xiaoshu_a;
非常值得注意的是,float型的小数只能提供7位有效数字。
所以当我使用%f输出数据时,最多只能显示6位小数位,不足6位的,会自动补0;而多于6位的,会四舍五入进位。
1.6—让我们运行下面的代码,来看看它的输出:
float a=3.14;
printf("%f",a);
float b=3.1415926;
printf("%f",b);输出结果
3.140000
3.141593那如果我们只想输出一个两位数小数,而不想要编译器自动在它末尾补的0,该怎么办呢?
这个时候,我们就可以在float型小数的插入符%f中百分号%的后面加上一个“小数点 + 小数位数”
例如 :%.2f,这样我们就可以只输出两位小数,我们定义一个浮点数变量并给它赋值3.14,然后打印输出它
float xiaoshua_a=3.14;
printf("%.2f",xiaoshu_a);
1.float,定义浮点数变量的关键字
2.xiaoshu_a,这个变量的变量名
3.=,赋值符号
4.3.14,一个小数
5.%.2f,格式化输出里面替代小数的符号,只输出两位小数
6.格式化输出里面要输出的变量
定义浮点型变量并赋值2.333,然后输出它
float b=2.333;
printf("%.3f\n",b);
输出结果
2.333
需要注意的是❗️,C语言是一门历史悠久的编程语言,那时候计算机的硬件资源(内存和CPU)都很宝贵,所以对数字的存储精度做了很多限制。
比如int整型变量的范围大约在-30000~30000,而float的范围在7位数字以内,也就是整数+小数部分的数字不要超过7位。
如果我们需要用到更大范围的数字的时候,我们后面会介绍到C语言中基于int和float的扩展数据类型。
为了简化记忆,我们只需要记住,int和float都有范围限制,超出了范围程序会报错,所以有时候程序出错了,我们可以看看是不是数字超出范围了。
我们知道了表示整型的int和表示浮点型的float,接下来我们学习C语言中代表字符的数据类型——字符型。
2.字符型
2.1-我们定义一个字符类型的变量letter_a,并赋值字符'm',并且打印它
char litter_a='m';
printf("%C",letter_a);
1.char,定义字符类型变量的关键
2.litter_a,一个变量的名字
3.=,赋值符号
4.'m',一个字符变量
5.%c,格式化输出里面的字符替代符
2.2-以这张图为例

int是定义整形变量的关键字,float是定义浮点型变量的关键字,当然,char就是定义字符型变量的关键字,char是字符的英文character的缩写。
同样的,在格式化输出里面,%d用来表示整型,%f用来表示浮点型,用来表示字符的就是%c,c是英文字母character的首字母。
同样的,在格式化输出里面,%d用来表示整型,%f用来表示浮点型,用来表示字符的就是%c,c是英文字母character的首字母。
2.3—定义字符型变量letter_b,并赋值'N',然后打印它:
char letter_b='N';
printf("%c\n",letter_b);
输出结果
N
2.4-到目前为止,我们一共学习了三种数据类型,表示整数的整型,表示小数的浮点型,和表示字符的字符型。
这三种数据类型在C语言中两种含义,第一种是应用于变量。用他们定义和声明某个变量的类型,具体含义是“这个变量的数据类型是定义好了的,不可改变的”。
int number_a=2023;
float number_b=3.1415;
char number_c='A';
第二种就是不应用变量的,用来单纯表示数据类型的,比如这三行代码都直接打印了数据本身。
printf("%d\n",2023);
printf("%f\n",3.1415);
printf("%C\n",'A');
3.常量
3.1-接下来我们就要学习一个和变量对应的概念常量。
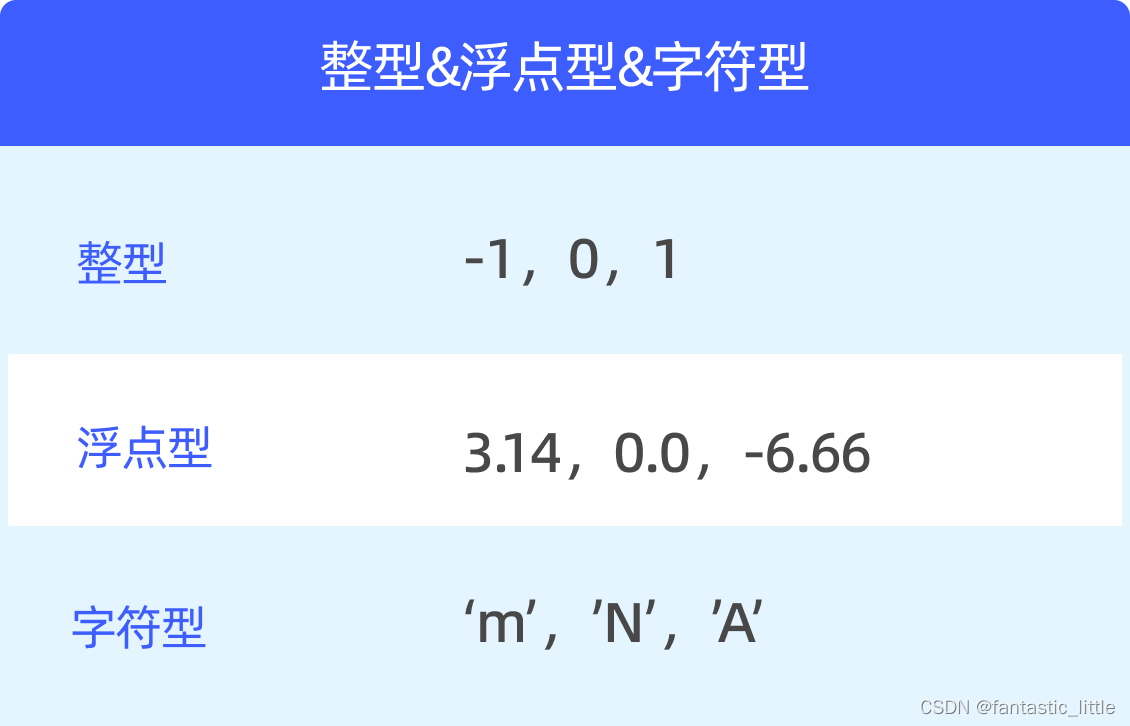
我们先来看三种不同类型的数据
A
2023
3.14151.字符型数据'A'
2.整型数据2023
3.浮点型数据3.1415
我们可以给一个变量进行赋值,比如下列代码,我们首先声明定义了一个变量this_year,并给他赋值了2023,然后第二行代码,我们修改了这个变量的值:
int this_year=2023;
this_yaer=2024;
而常量意思是,一个不可改变的量,比如我们不能写这样的代码,因为2023是一个常量,它不能再被赋值了。
2023=2024;
3.2以从盒子中拿球为例

就像我们可以给一个空盒子里面放入一个球。以及从盒子里拿出一个球,再放入另外一个球,这就是变量的赋值。
但是我们无法把一个球放入另外一个球里面,这个球就像一个常量,它是实心的,不具备容纳其他东西的功能。
同样的,我们也不能写这样的代码:
'a'="B";
3.3-我们还可以给变量加个前缀const,让这个变量变成常量,这时候这个变量的值就不能再改变了。const的意思也是不可改变的。
cost int a=2023;
这种被const改变了属性的变量,依旧可以被访问,比如打印出来,这时候代码会正常运行。
cost int a=2023;
printf("%d\n",a);
但它的值无法被改变,所以下面这个代码就会报错。
cots int a=2023;
a=2024;
4.易错点

eg:
浮点型数据对应的插入符是 %f
整型数据对应的插入符是 %d
字符型数据对应的插入符是 %c
eg:
字符型变量赋值时,记得要用英文的单引号''把字符括起来
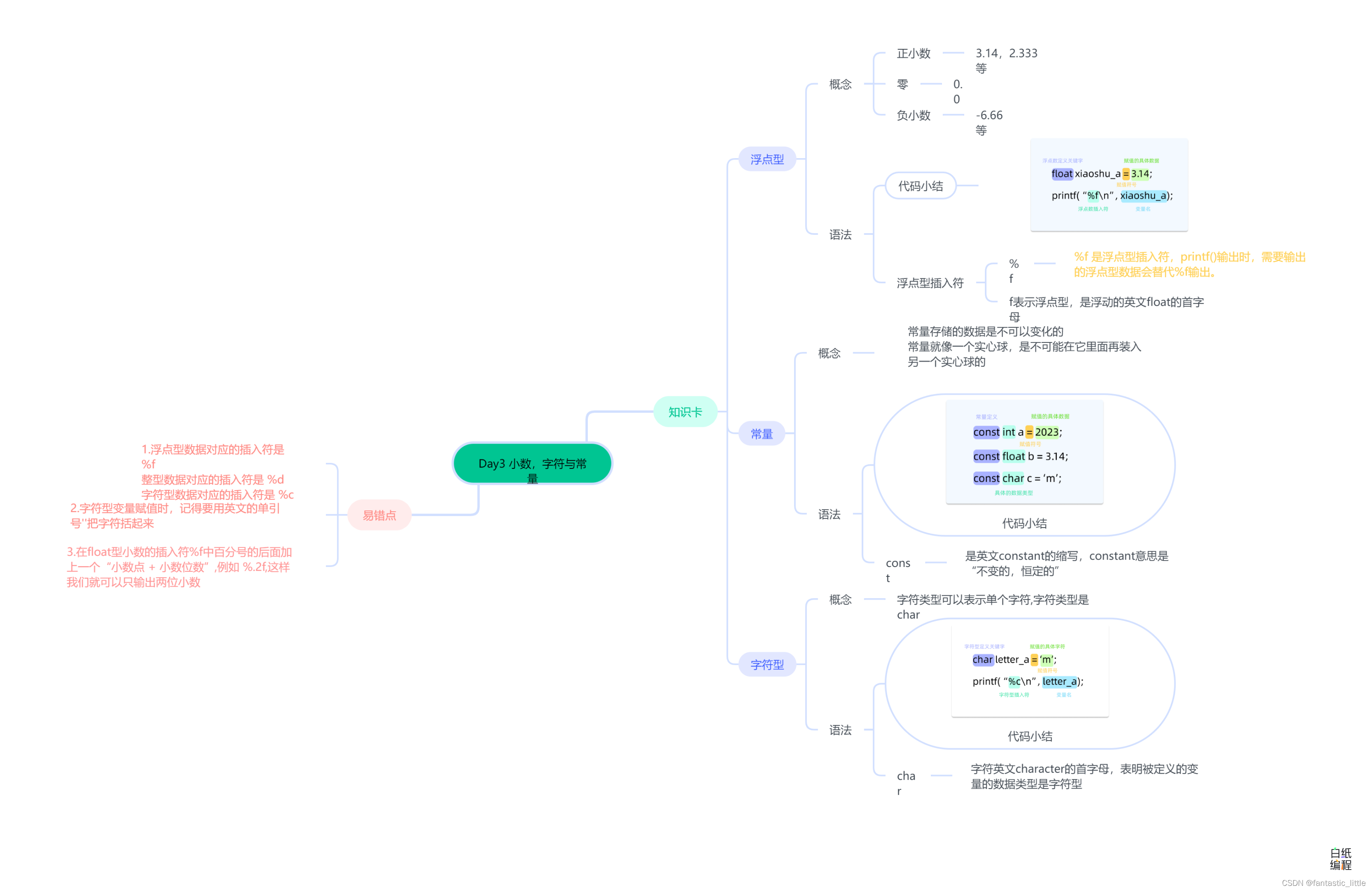
5.思维导图
在撰写这篇文章时,我参考了《白纸编程》这个app的观点和思想,我要感谢他们对我的启发和帮助。