Infrared and visible image fusion via gradientlet filter

（基于梯度波滤波器的红外与可见光图像融合）

本文从亮度和梯度分离的角度出发，提出了一种基于模糊梯度阈值函数和全局优化的图像滤波器梯度小波滤波器。它可以在保持图像的整体亮度和边缘渐变的同时，去除小的渐变纹理和噪点。基于梯度波滤波和图像显著性，提出了一种新的红外与可见光图像融合方法，克服了传统融合图像存在的对比度低、边缘模糊和噪声等问题。首先，利用梯度波滤波器将源图像分解为近似层和残差层，前者反映了源图像的整体亮度，没有边缘模糊和噪声，后者反映了源图像的小梯度纹理和噪声。其次，根据近似层和残差层的特点，提出了对比度显著图和梯度显著图，并构造了相应的权值矩阵。最后，基于先前获得的子图像和权重矩阵进行融合和重构，得到融合图像。

介绍

提出了一种新的图像滤波器–梯度波滤波器，并在多尺度变换融合的框架下，设计了一种基于梯度波滤波器和图像显著性的融合算法。通常，图像由亮度分布和小梯度变化组成，前者反映图像的对比度和空间结构，后者反映纹理和噪声，即“亮度分布+小梯度变化=图像”。为了保持图像的对比度，我们从分离图像亮度和小梯度的角度设计了一个滤波器。传统的基于局部加权平均的滤波分解由于亮度的离散性不可避免地会导致边缘模糊，因此需要采用全局优化的方法将滤波器设计为边缘保持滤波器。为此，提出了基于模糊梯度阈值函数和全局优化的梯度波滤波器。它用于将源图像分解为近似层和残差层。近似层反映了源图像的整体亮度分布，没有边缘模糊和噪声，并保存了图像的对比度和空间结构信息。残差层反映了源图像的微小梯度变化，并保留了原始图像的纹理信息和噪声。

为了保持图像的对比度信息，避免噪声对融合图像的影响，根据近似层和残差层的不同特点，并考虑噪声的影响，设计融合规则。首先，由于近似层保留了原始图像的对比度信息且无噪声，通过映射近似层的对比度显著性，构造相对平滑的近似层权重矩阵。这些矩阵用于近似层的融合，以便在不引入噪声的情况下保持图像对比度。其次，考虑到残差层噪声相对较强的特点，通过映射源图像的梯度显著性而非残差层的梯度显著性来构造残差层的锐化权值矩阵。利用这些矩阵对残差层进行融合，既保留了图像的纹理信息，又减少了噪声对融合图像的影响。最后，通过重构得到融合图像，该融合图像具有较好的对比度和细节信息，并且边缘模糊和噪声的影响较小。

贡献

1）提出了一种基于模糊梯度阈值函数和全局优化的梯度波滤波器，该滤波器能够在保持图像整体亮度和边缘梯度的同时，有效地去除小梯度纹理和噪声。
2）针对红外与可见光图像融合中存在的对比度低、边缘模糊和噪声等问题，在提出的梯度波滤波器和图像显著性的基础上，提出了一种新的红外与可见光图像融合方法。

相关工作

多尺度变换框架：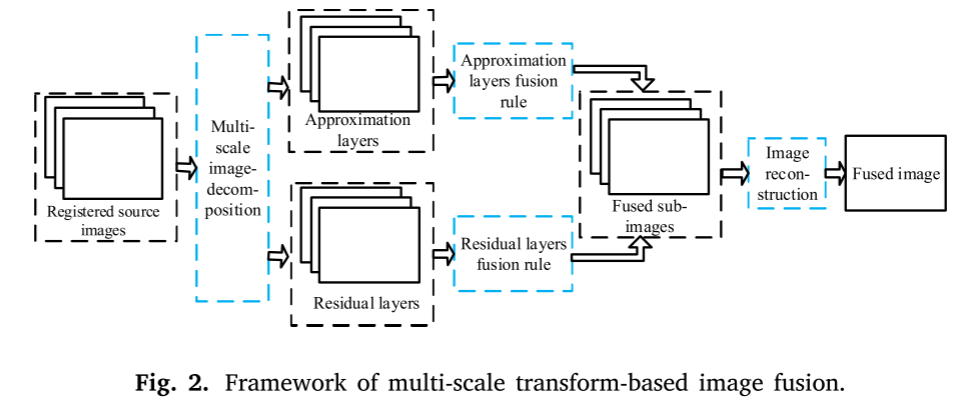
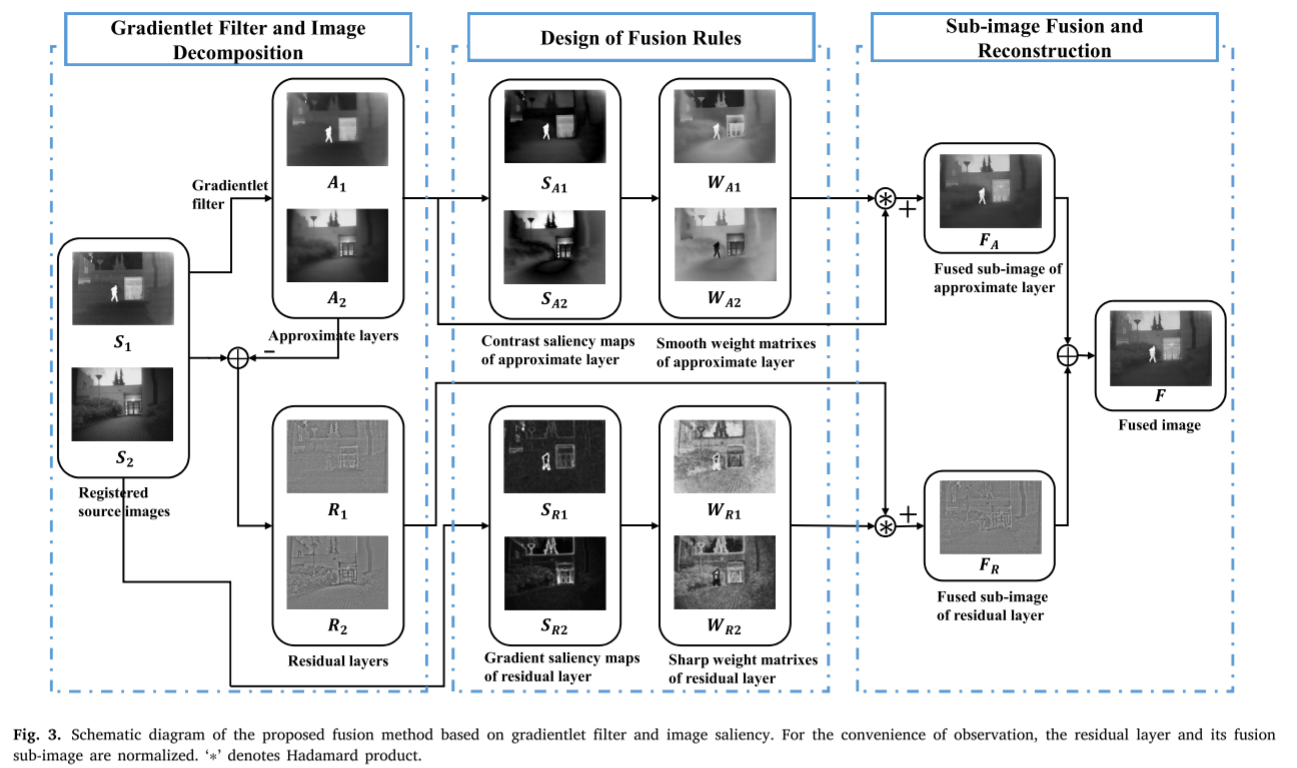
如图2所示，多尺度变换融合通常包括三个步骤。首先，将配准后的源图像分解为一系列称为近似层和残差层的子图像。其次，根据近似层和残差层的特点，设计了相应的融合规则，用于不同尺度下的信息融合。最后，对融合后的子图像进行重构，得到最终的融合图像。

随着小波理论的成熟，小波变换也被应用到多尺度分解中。利用小波的信号分解特性，将图像分解为不同频带的子图像，进行多尺度融合。例如，Niu等人提出了基于目标区域分割和离散小波变换的机载红外与VS图像融合方法;该方法使得融合图像能够在保留背景信息的同时获得丰富的目标信息并因此产生用于空中目标感知的上级融合图像。Zou等人提出了一种基于提升小波域的图像融合方法来提高同一场景的VS和IR图像的融合效果。Chai等人提出了一种基于四元数小波变换和多特征的多模态图像融合方法，并将其应用于多聚焦图像、医学图像、IR-VS图像和遥感图像。然而，小波变换不能捕捉图像丰富的方向信息。因此，提出了轮廓波变换来克服该缺点。Meng等人提出了一种IR和VS图像融合算法，该算法将目标区域检测与非下采样轮廓变换（NSCT）相结合以提高融合图像的质量。
随着边缘保持滤波器技术的不断发展，基于边缘保持(edge-preserving)滤波器的融合算法也被提出。由于边缘保持滤波器的优点，基于它们的算法通常产生良好的边缘特征。Li等人提出了一种融合算法（GFF）基于引导滤波器（GIF）该算法保持了图像的空间一致性，适用于多光谱、多聚焦、多模式、多曝光图像的融合。Ma等人提出了一种基于高斯滤波器和滚动制导滤波器（RGF）的方法，该方法有效分离了源图像的尺度，提高了图像的细节信息，有效降低了融合图像的假轮廓。Hu等人提出了一种多尺度方向双边滤波器，并将其应用到多传感器图像融合算法中，使融合后的图像能够有效地保留方向信息和几何结构。

方法

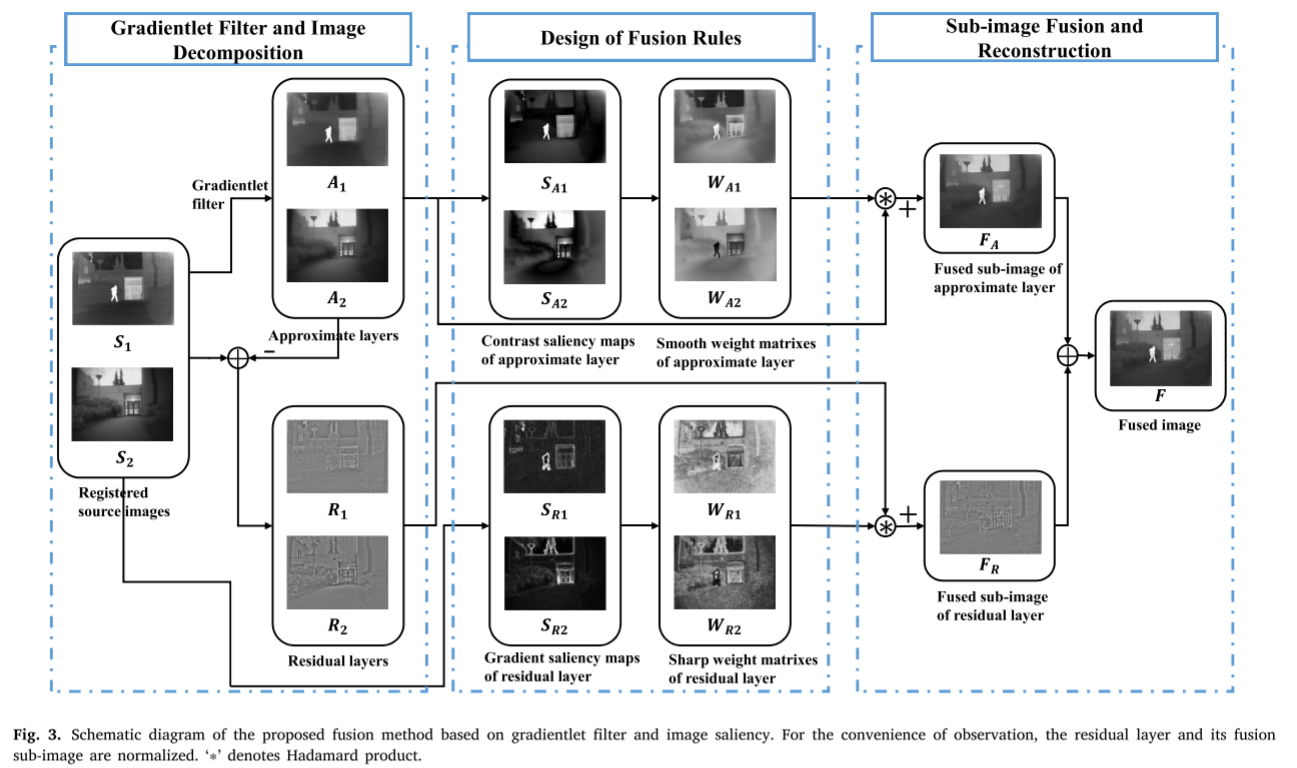
我们的融合策略框架如图3所示。首先，我们提出了一种梯度波滤波器，并用它将源图像𝑆₁（IR图像）和𝑆₂（VS图像）分解为两部分：近似层（𝐴₁，𝐴₂）和残差层（𝑅₁，𝑅₂）。其次，根据近似层和残差层的不同特征，构造对比度显著图（𝑆_𝐴1，𝑆_𝐴2）和梯度显著图（𝑆_𝑅1，𝑆_𝑅2）。同时，采用不同的权值构造方法，得到近似层**（𝑊_𝐴1，𝑊_𝐴2）的平滑权值矩阵和残差层（𝑊_𝑅1，𝑊_𝑅2）的尖锐权值矩阵**。最后，对子图像和相应的权矩阵求出Hadamard积，并将其相加，得到相应的近似层融合子图像（𝐹_𝐴）和残差层融合子图像（𝐹_𝑅）。最终的融合图像（𝐹）是通过将融合后的子图像直接相加而获得的。在以下算法中，除非另有说明，否则像素值范围为0到1。

Gradientlet filter

Problem formulation

对于给定的输入图像，利用全局优化方法构造一个边缘保持滤波器，该滤波器在保持输入图像亮度分布的同时，去除图像中的小梯度变化。一方面，为了保持图像亮度分布，我们应该限制输出图像，使得其像素强度分布类似于给定输入图像的像素强度分布。因此，由𝐿₂范数定义的以下平方总误差𝑒₁应尽可能小：另一方面，为了抑制小的图像梯度，我们应该限制滤波后的输出图像的总梯度𝑒₂，其定义如下：
通过组合Eqs.(1)和（2），我们将滤波问题公式化为最小化以下目标函数：

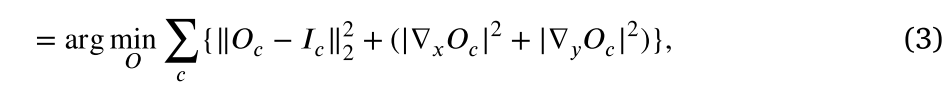
其中第一项是用于保持输入图像的亮度分布的数据保真度项，第二项是用于滤波图像梯度的梯度去除项。然而，通常，图像的纹理和噪声梯度相对小于其边缘梯度。在Eq.(3)中的梯度去除过程中，纹理或噪声梯度和边缘梯度被无区别地去除，因此不能达到去除小梯度纹理和噪声而保持边缘的目的。因此,它需要修改梯度删除条目,以便它保留边缘梯度大,同时去除小梯度噪声和纹理信息尽可能多。为此，我们设置一个阈值来区分边缘和纹理或噪声，并根据梯度阈值设计一个惩罚系数。特别是,边缘梯度大于梯度阈值,应该保存尽可能多的与一个小惩罚因子。噪音或纹理梯度小于梯度阈值,应该尽可能地消除大惩罚因子。根据上述要求,处罚系数P可以设计如下:

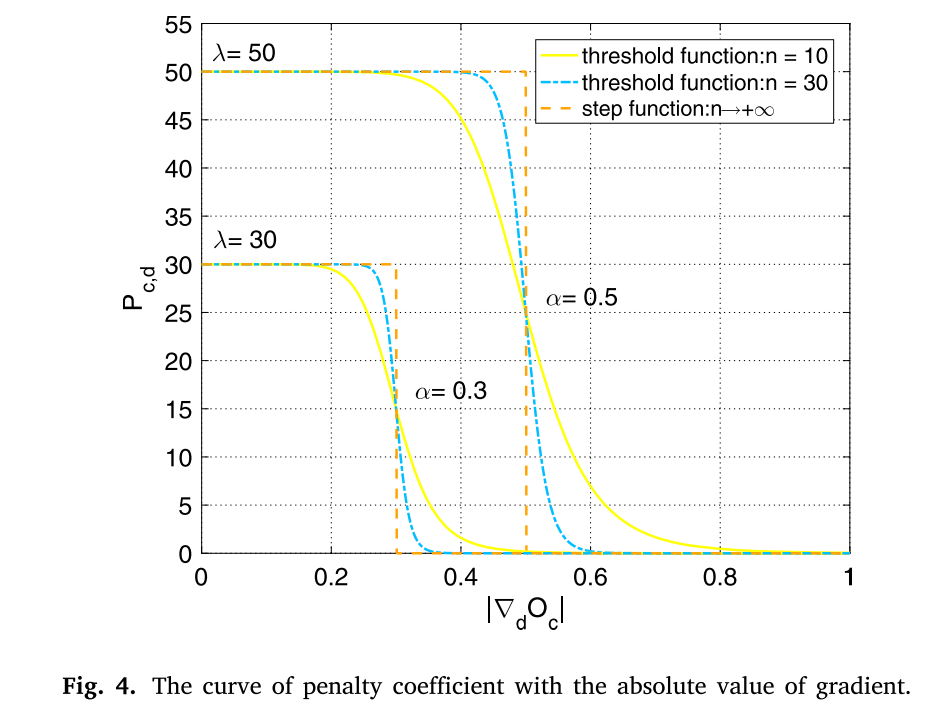
如图4所示，对于梯度低于梯度阈值的纹理或噪声，惩罚系数较大，最大值为𝜆。对于梯度大于梯度阈值的边缘，罚系数较小，最小值为零。在梯度阈值附近𝛼，罚系数随梯度的增大而逐渐减小，下降速率由控制𝑛;越大𝑛，斜率越大，阈值函数越接近阶梯函数。当𝑛接近正无穷大时，阈值函数变为阶跃函数。在我们的方法中，阶跃函数不直接用作阈值函数，因为在实际情况中，代表纹理或噪声的小梯度和代表边缘的大梯度构成模糊隶属度概念而不是确定隶属度概念。也就是说，不存在明确的边界，而是注意到类似于隶属度的模糊边界。
最后，我们将Eq.（3）中表示的惩罚系数与Eq.（4）中表示的惩罚系数进行组合。其中梯度移除项在为了获得最终的目标函数：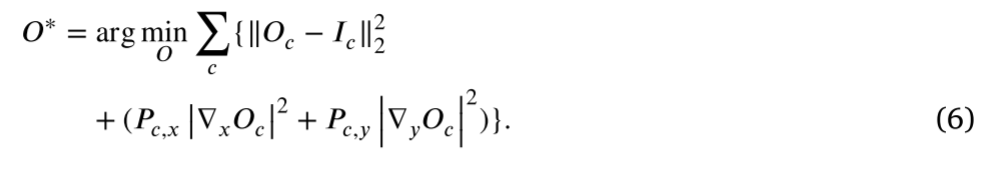

消融实验

略

为了清晰起见，我们在Alg.1中总结了上述滤波算法的整个过程。该过滤器被命名为gradientlet过滤器，并表示为𝐺𝑙𝑒𝑡𝐹（𝐼，𝑓，𝛼，𝜆，𝑛）。

Image decomposition

如图3所示，采用设计的梯度波滤波器分解源图像的亮度分布和小梯度变化𝑆_𝑛。通过梯度波滤波器对源图像进行滤波以获得近似层𝐴_𝑛：

从源图像中减去近似层以获得相应的残差层𝑅_𝑛：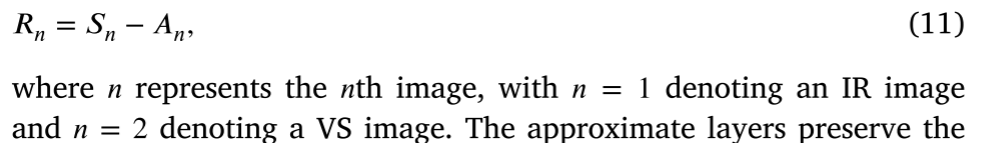
近似层保留了源图像的亮度和能量分布。此外，它们包含源图像的对比度和结构信息，没有噪声和边缘模糊，并且它们体现了源图像的整体外观。与近似层相比，残差层几乎没有亮度和能量分布，主要反映小的梯度变化，包括源图像的纹理信息和噪声。

Design of fusion rule

系数的融合规则组合策略调整基于子图像特征。他们是重要的突出感兴趣的信息(图像和图像对比度和图像细节)抑制或消除不重要信息(噪音)。常用的融合规则是直接平均加权平均,choosemax等等。然而，大多数传统的融合规则倾向于根据它们的空间尺度来保留细节，并且没有充分考虑对比度和噪声。因此，目标可能不显著，并且细节信息模糊和丢失，从而影响视觉效果和目标检测。因此，为了保持图像的对比度信息，避免噪声对融合图像的影响，根据近似层和残差层的不同特点设计融合规则，并考虑对比度和噪声问题。一方面，将近似层的对比度显著性映射和相应的平滑权值矩阵应用于后续的近似层融合，以保持图像对比度而不引入噪声。另一方面，我们认为源图像中的噪声比例通常小于残差层中的噪声比例。该算法利用原始图像的梯度显著性映射和对应的锐化权值矩阵代替残差层进行后续的残差层融合，以保持图像的纹理并降低噪声。

Saliency map and weight matrix of approximate layer

近似层反映源图像的亮度分布，其包含对比度信息，并且通常不受噪声影响。因此，为了保持对比度，我们根据近似层的亮度分布来构造近似层的对比度显著图。通常，图像对比度是指图像中最高和最低亮度级之间的差。亮度差异越明显，对比度越高。因此，我们可以推断，像素值相对于图像均值越亮或越暗，其对图像对比度的贡献越大，对比度显著性越强。因此，采用𝐿₂范数来度量像素值与平均值的偏差，并表示每个像素的重要性。通过对整个近似层图像执行该操作𝐴_𝑛，可以获得近似层的对比度显著图𝑆_𝐴𝑛，即，

其中𝑚𝑒𝑎𝑛（·）表示图像矩阵的均值，采用𝐿₂范数消除符号的影响，𝑛𝑜𝑟𝑚（·）函数拉开显著值的距离，使显著图越来越有效：

可以对近似层的显著图进行如下操作，直接得到近似层的权重矩阵𝑊_𝐴1和𝑊_𝐴2：

Eq.(14)显示了仅当两个源图像的对比度显著不同时（其中一个接近于0而另一个接近于1），权重矩阵被构造成接近于最大选择方法。然而，在大多数情况下，权重矩阵接近于平均方法。因此，如图3所示，近似层的最终权重矩阵在空间平滑性方面与近似层相似。

Saliency map and weight matrix of residual layer

由于残差层主要反映了源图像的微小梯度变化，包括纹理信息和噪声，因此可以根据图像梯度构造残差层的梯度显著图。一些基本的梯度算子，如Robert交叉梯度算子、Prewitt算子和Sobel算子，通常被用来获得图像的梯度图。然而，由于缺乏对称中心，难以实现均匀大小的模板，并且通常不使用Robert的交叉梯度算子。同时，Sobel算子比Prewitt算子能更好地平滑图像中的噪声。因此，我们使用Sobel算子来构造梯度映射。同时考虑到源图像中噪声所占的比例小于残差层，并且源图像包含丰富的纹理信息。使用Sobel算子代替残差层从源图像中提取梯度特征𝑆_𝑛，得到梯度图𝐺_𝑛，可以有效地保留纹理信息，降低噪声的影响：

其中𝑆𝑜𝑏𝑒𝑙（·）表示对原始图像的每个像素的以下操作：
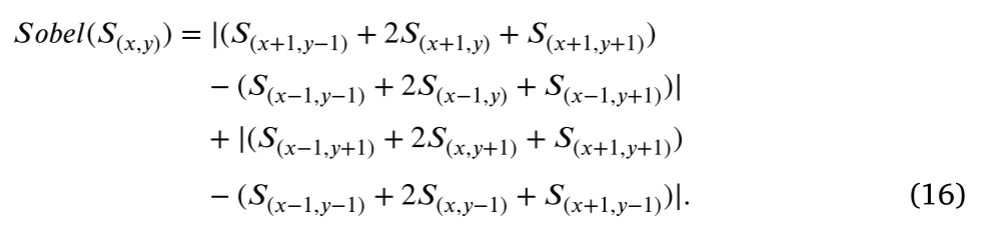利用高斯滤波器对得到的梯度图像进行扩散𝐺_𝑛，扩大梯度对权重的影响范围，得到最终的梯度显著图𝑆_𝑅𝑛：

其中𝐺𝑎𝑢𝑠𝑠𝑖𝑎𝑛（·）是高斯滤波器，𝛿是其标准差，𝑟是滤波器中高斯模板的半径。此处，𝛿和𝑟通常设为5。
对于残差层的显著性图𝑆_𝑅𝑛，残差层的权重图𝑊_𝑅1和𝑊_𝑅2通过以下步骤获得：

与近似层的权值矩阵不同，仅当两幅源图像的梯度显著性差异较小时，残差层的权值矩阵才近似于平均法;在其它情况下，矩阵的构造接近于选择最大值方法。因此，如图3所示，最终的残差层的权重矩阵具有与残差层相同的高空间频率。

Image fusion and reconstruction

通过以上步骤，我们得到了近似层和残差层的子图像，以及相应的权值矩阵。接下来，我们需要融合和重建子图像。如以下等式所示，将Hadamard乘积应用于子图像和对应的权重矩阵，并且将结果求和以获得对应的融合子图像：其中，𝐹𝐴为近似层融合的结果，𝐹_𝑅为残差层融合的结果，𝑁为原始图像数（本工作中𝑁= 2），* 表示Hadamard积。最后，𝐹通过近似层和残差层的融合子图像重构得到融合图像：

如图3所示，得到的近似层融合子图像整合了源图像的整体外观，保持了图像的对比度信息，不存在边缘模糊和噪声问题。残差层融合子图像融合了源图像的纹理信息，减少了模糊和噪声。因此，重建得到的最终融合图像具有高对比度和零边缘模糊。该方法有效地降低了噪声对图像细节的影响，保留了图像的目标显著性和纹理信息。整个算法流程在Alg.2.