文章目录
- 引言
- 一、整数规划问题的提出
- 1.1 整数规划的数学模型
- 1.2 整数规划问题的求解
- 二、分支定界法
- 2.1 分支与定界
- 2.2 基本求解步骤
- (一)初始化
- (二)分支与分支树
- (三)定界与剪枝
- (四)搜索迭代
- 2.3 分支定界法的应用
- 写在最后
引言
整数规划是数学规划的一个重要分支,在实际中有非常广泛的应用背景,例如著名的指派问题、背包问题和旅行商问题。同时,它又是最难求解的问题之一,所以整数规划领域一直都比较活跃。
一、整数规划问题的提出
1.1 整数规划的数学模型
线性规划的一个重要假设是决策变量可取非整数的连续值,然而这一假设在很多情况下是不满足的。一般称对决策变量有整数要求的数学规划问题为整数规划问题(Integer Programming,可简称 IP )。
根据变量取值的限制形式,整数规划又分为三种:
- 纯整数规划(IP):所有决策变量都取整数值。
- 混合整数规划(MIP):部分决策变量取整数值。
- 0-1 整数规划(BIP):整数变量只能取 0 或 1 。其又可分为纯 0-1 和混合 0-1 整数规划。
显然,如果把整数限制去掉,整数规划就成为了线性规划,此线性规划问题称为整数规划的线性规划松弛问题。
1.2 整数规划问题的求解
既然整数规划问题只是加了一个整数约束,那可不可以先求松弛问题的最优解出来,让最优解取整,就得到整数规划的最优解呢?
答案是否定的,如果只是对最优解进行取整,有可能与最优整数解相差甚远,而且有可能取整后不满足约束条件,不可行。

但是我们可以得到如下整数规划的最优解和松弛问题的最优解之间的关系:
对于求 m a x max max 问题,松弛问题的最优目标函数值 ≥ \geq ≥ 整数规划问题的最优目标函数值。
这也很好理解,松弛问题的可行解包含了整数规划的所有可行解,自然最优目标函数值不会小于整数规划问题的最优值。
如果线性规划松弛问题的可行域有界的话,整数规划的解是有限的。理论上讲,可以通过穷举法,把每个点都算出来比较大小。不过对于整数变量较多的问题,计算时间相当大,无法派上实际用场。
目前比较成熟的求解方法是分支定界法和割平面法,下面依次来介绍一下。
二、分支定界法
2.1 分支与定界
通过之前的讨论,我们可以发现如下几个事实:
- 如果求解一个整数规划的线性规划松弛问题,恰好得到最优解都取整数,那么,这个解也一定是相应整数规划问题的最优解。
- 如果松弛问题的最优解不是整数,那么,整数规划问题的最优解一定不会比它好。也就是说,对于求最大的问题,线性规划松弛问题的最优解值是整数规划问题解值的上界。
- 如果求解过程中已经出现一个整数解,那么,整数规划问题的最优解值一定不会比它差。也就是说,求出的一个整数解值是整数规划问题解值的一个下界。
如果用
z
0
z_0
z0 表示线性规划松弛问题的最优解值,用
z
i
z_i
zi 表示找到的某个整数解值,
z
∗
z^*
z∗ 为最优整数解值,
z
‾
\underline{z}
z 表示下界,
z
‾
\overline{z}
z 表示上界,则极大化整数规划问题的最优整数解
z
∗
z^*
z∗ 满足如下关系:
z
‾
=
z
i
≤
z
∗
≤
z
0
=
z
‾
\underline{z}=z_i \leq z^* \leq z_0 = \overline{z}
z=zi≤z∗≤z0=z
如果能找到一种方法,不断降低上界,提高下界,最后使得上界等于下界,就可以搜索到最优整数解。分支定界法就是按照这一原理设计的。它从求解线性规划松弛问题开始,将松弛问题分成许多小的子域,这一过程称为分支;通过分支和找到更好的整数解来不断修改问题的上下界,这一过程称为定界,这就是分支定界法名称由来。
2.2 基本求解步骤
(一)初始化
对给定的整数规划问题,放松整数约束,求解它的线性松弛问题。如果得到的解是整数,该解即为整数规划的最优解。否则,所得到的线性规划松弛解作为整数规划问题最优解的初始上界。初始下界一般可设为负无穷。
(二)分支与分支树
从任何一个问题或子问题的不满足整数要求的变量中,选出一个进行处理的过程称为分支。分支通过加入一对互斥的约束将一个(子)问题分解为两个受到进一步约束的子问题,并强迫不为整数的变量进一步逼近整数值。
举个例子,比如松弛问题最优解为 x 1 = 4.81 , x 2 = 1.82 x_1=4.81,x_2=1.82 x1=4.81,x2=1.82 。可以先选中变量 x 1 x_1 x1 ,其整数部分为 4 4 4 ,则可以添加一个约束为 x 1 ≤ 4 x_1 \leq 4 x1≤4 ,作为一个子问题。添加约束 x 1 ≥ 5 x_1 \geq 5 x1≥5 作为新的子问题。利用第 4 章的内容,添加新约束条件可以不重新计算,分别求出两个子问题的最优解。
分支砍掉了 4 4 4 和 5 5 5 之间的非整数域,缩小了搜索的区域。
子问题若不满足整数要求,还可继续向下进行分支,分支可以形成一个倒置的分支树。树的根节点是线性规划松弛解,它有两个后续子节点,每个子节点又会有两个子节点,分支可继续进行下去,直到找到一个整数节点或该节点不可行时为止。

为方便起见,我们称前导节点称为父节点,后续节点为子节点。分支树上的每一个节点都代表一个子问题,如果该子问题还没有求解过,称该节点为打开节点,已求解过的节点称为关闭节点。
(三)定界与剪枝
通过不断地分支和求解各个子问题,分支定界发不断修正其上下界的过程称为定界。上界通常由各打开节点中最大的目标函数值来确定。,下界则由已经找到的最好的整数解来确定。求解任何一个子问题都有以下三种可能结果:
- 子问题无可行解。此时无需继续往下分支,该节点因为不可行而关闭。因为往下分支的子问题是添加了约束条件的,肯定同样不可行。
- 得到一个整数解,则不必往下分支,该节点因为有一个整数解也被关闭。如果该整数解是目前最好的整数解,则被记录下来,并且它的值作为新的下界。
- 得到一个非整数解时才有可能进一步向下分支,是否向下分支取决于该节点的目标函数值是否优于下界(目前最好整数解值)。分支树的一个重要特点是各节点的目标函数严格有序,即子节点的目标函数值一定不会大于父节点的目标函数值。所以只有当该节点的目标函数值大于下界时,才有必要向下分支,因为后续节点才有可能有更好的整数解。因此存在以下两种情况:
a)目标函数值大于下界,继续向下分支。
b)目标函数值小于等于下界,因剪枝而关闭。
(四)搜索迭代
每完成一次分支过程即完成一次搜索。在搜索的过程中,每当下界被修改后,都应检查所有打开的节点中,那些目标函数值小于新下界的节点。这些节点是要被剪掉的,因此而关闭。所有节点关闭表明搜索已经完成。如果此时没有找到任何整数解,则该问题没有整数解;否则搜索过程中得到的最好整数解就是该问题的最优解。
2.3 分支定界法的应用
光有文字这样干说有点抽象,下面结合一个具体例子来说明分支定界法的具体使用。

解: 先不考虑整数限制,利用单纯形法求解松弛问题
B
B
B,其最优单纯形表为:
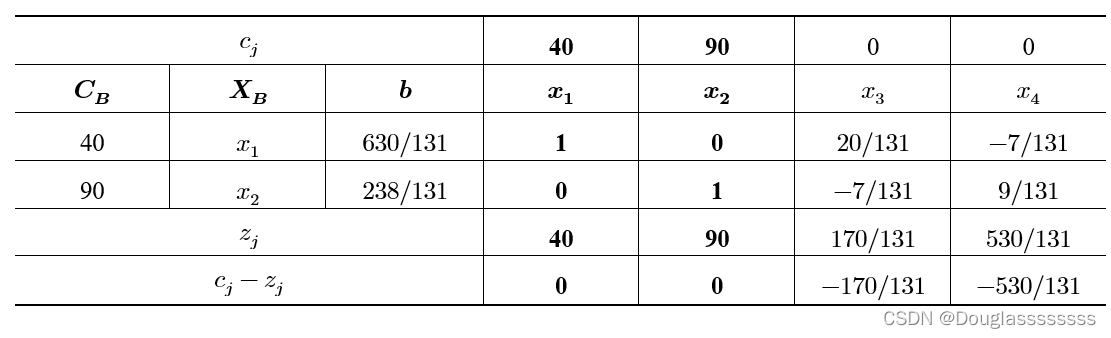
得到最优解为: x 1 = 4.81 , x 2 = 1.82 , z 0 = 356 x_1=4.81,x_2=1.82,z_0=356 x1=4.81,x2=1.82,z0=356 显然,两个决策变量均不符合整数约束条件。此时可记 z 0 z_0 z0 为最优目标函数值的上界 z ‾ \overline{z} z 。当 x 1 = x 2 = 0 x_1=x_2=0 x1=x2=0 时,符合整数要求,此时 z = 0 z=0 z=0 ,可作为下界,因此整数规划问题 A A A 的最优解 z ∗ z^* z∗ 满足 0 ≤ z ∗ ≤ 356 0 \leq z^* \leq 356 0≤z∗≤356 。
对问题 B B B 增加一个约束条件 x 1 ≤ 4 x_1 \leq 4 x1≤4 ,构成问题 B 1 B_1 B1 。增加约束条件 x 1 ≥ 5 x_1 \geq 5 x1≥5 ,构成问题 B 2 B_2 B2 。将约束条件化为等式后补加到最优单纯形表中,令新增加的松弛变量为基变量,继续求解。可得到两个子问题的最优解如下表所示。

问题 B 1 B_1 B1 目标函数值较好,可更新上界 z ‾ = z 1 = 349 \overline{z}=z_1=349 z=z1=349 ,由于未出现整数解,因此下界仍为 0 。因此整数规划问题 A A A 的最优解 z ∗ z^* z∗ 满足 0 ≤ z ∗ ≤ 349 0 \leq z^* \leq 349 0≤z∗≤349 。
子问题 B 1 B_1 B1 的目标函数值较大,故先将其进行分支,添加约束条件 x 2 ≤ 2 x_2 \leq 2 x2≤2 ,得到子问题 B 3 B_3 B3 ,添加约束条件 x 2 ≥ 3 x_2 \geq 3 x2≥3 ,得到子问题 B 4 B_4 B4 。分别进行求解,可得到如下结果。

可知, B 3 B_3 B3 已经满足整数要求,不必继续分支,且为第一个整数解,故直接可更新下界为 z ‾ = z 3 = 340 \underline{z}=z_3=340 z=z3=340 。问题 B 4 B_4 B4 由于最优解值小于下界,故直接关闭。问题 B 2 B_2 B2 的最优解值大于下界,可继续进行,并更新上界为 z ‾ = z 2 = 341 \overline{z}=z_2=341 z=z2=341 。因此整数规划问题 A A A 的最优解 z ∗ z^* z∗ 满足 340 ≤ z ∗ ≤ 341 340 \leq z^* \leq 341 340≤z∗≤341 。
对问题 B 2 B_2 B2 分别添加约束条件 x 2 ≤ 1 x_2 \leq 1 x2≤1 和 x 2 ≥ 2 x_2 \geq 2 x2≥2 ,分别构成问题 B 5 B_5 B5 和 B 6 B_6 B6 。进行求解,得到如下结果。
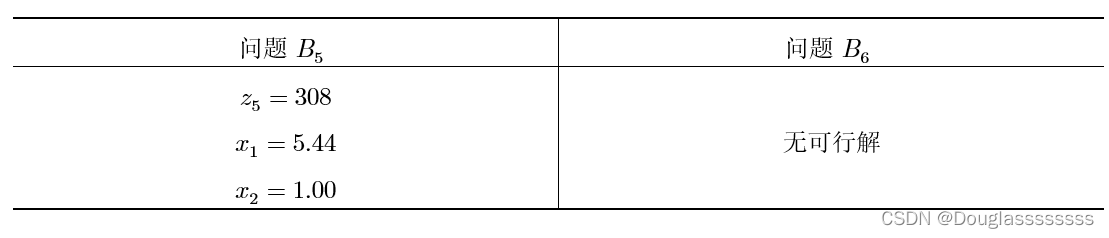
z
5
z_5
z5 由于小于下界,故问题
B
5
B_5
B5 关闭。问题
B
6
B_6
B6 因不可行而关闭。
至此,所有节点均已关闭,其分支过程如下图所示。

得到最优整数解为
x
1
=
4
,
x
2
=
2
,
z
∗
=
340
x_1=4,x_2=2,z^*=340
x1=4,x2=2,z∗=340 ,即为原问题
A
A
A 的最优解。
写在最后
分支定界法可求解纯整数规划和混合整数规划问题,计算量比穷举法小,更为优越。
整数规划求解方法还有割平面法,我们下一篇文章再来介绍。另外,0-1 型整数规划求解法也将会放在第 5 章中。








![[杂症]PLSQL很卡](https://img-blog.csdnimg.cn/75a235ddae9b485894462e23e8d032b9.png)