Problem - 1857G - Codeforces 
题意：

 

思路：

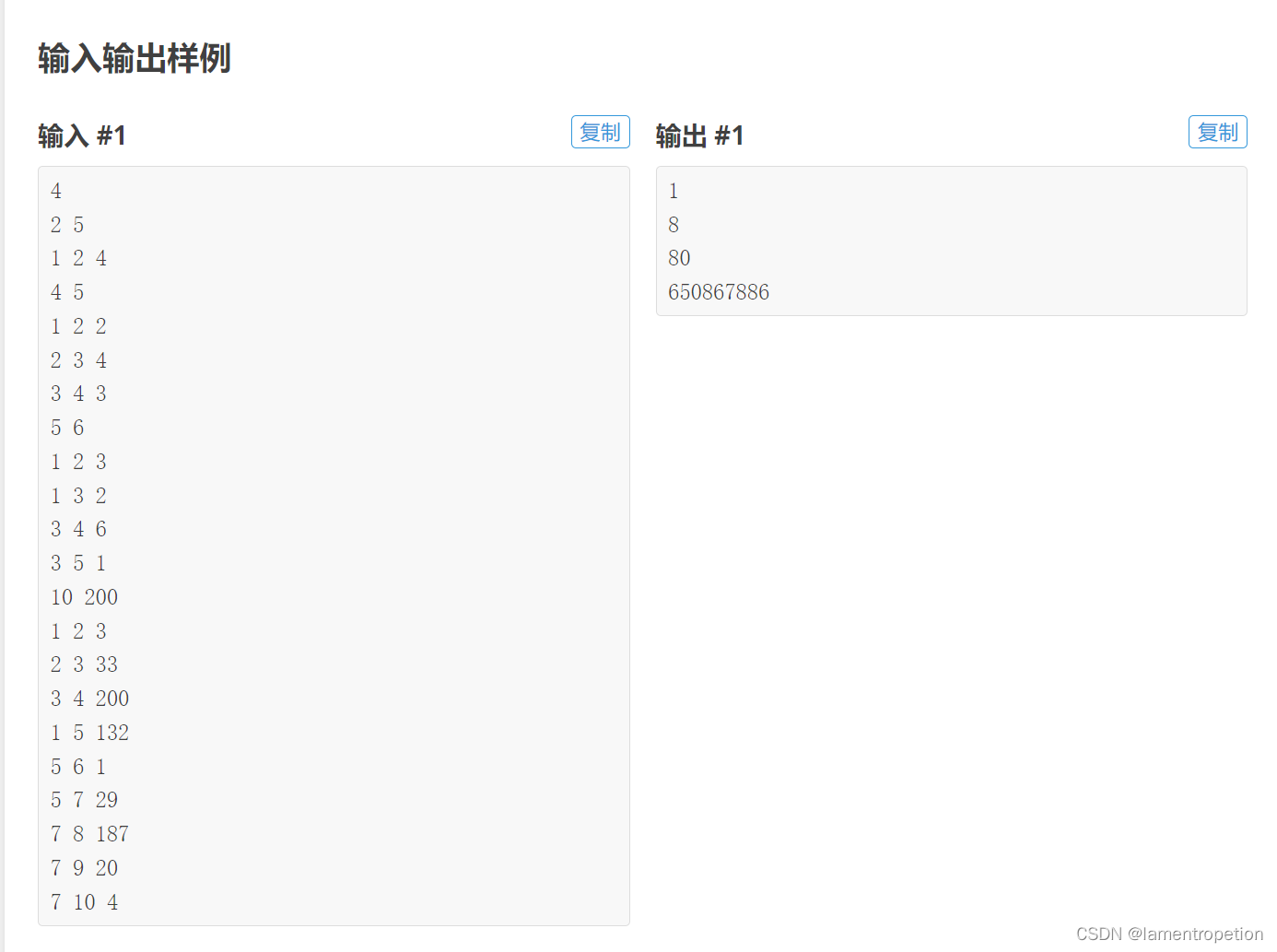
首先观察一下样例： 

 

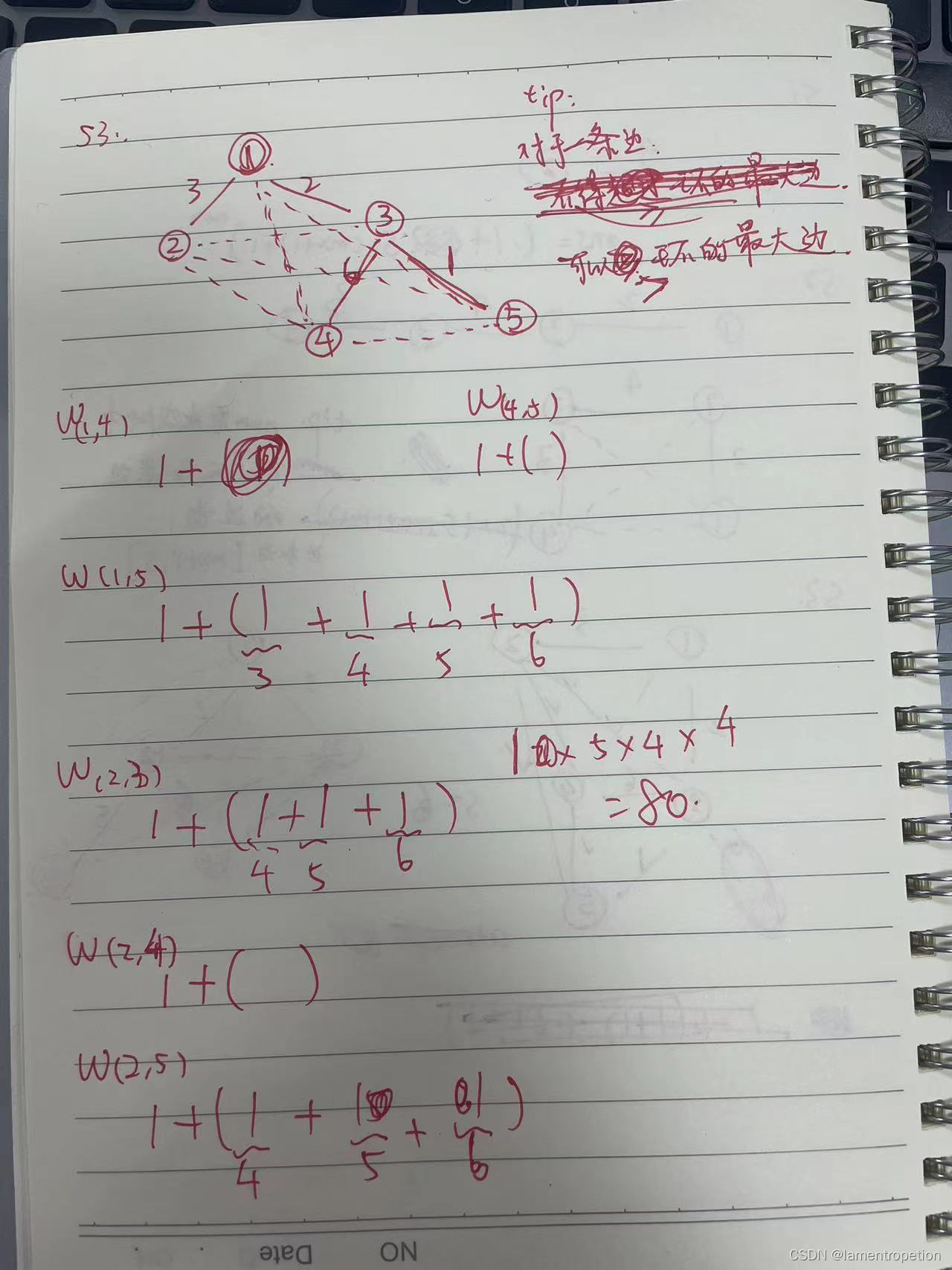
可以发现对于每一对点，贡献是 s - 这对点对应的环的最大边 + 1

那么这样就有了 n^2 的做法

然后，根据惯用套路，枚举树上的点对问题可以转化为枚举边，按边去算贡献

在Kruskal的过程中，一条边是作为最大边出现的，贡献是

qpow((s - V[i][0] + 1), ((sz[find(V[i][1])] * sz[find(V[i][2])] - 1)))) % mod

Code：

#include <bits/stdc++.h>

#define int long long

using i64 = long long;

constexpr int N = 2e5 + 10;
constexpr int mod = 998244353;

int f[N], sz[N];

int find(int x) {
    return f[x] = (x == f[x] ? x : find(f[x]));
}
void join(int u, int v) {
    int f1 = find(u), f2 = find(v);
    if (f1 != f2) {
        f[f1] = f2;
        sz[f2] += sz[f1];
    }
}
int qpow(int a, int b) {
    int res = 1ll;
    while(b) {
        if (b & 1) res = (res * a) % mod;
        a = (a * a) % mod;
        b >>= 1;
    }
    return res;
}
bool cmp(std::array<int,3> x, std::array<int,3> y) {
    return x[0] < y[0];
}
void solve() {
    int n, m, s;
    std::cin >> n >> s;

    for (int i = 1; i <= n; i ++) {
        f[i] = i;
        sz[i] = 1;
    }

    std::vector<std::array<int,3> > V;
    for (int i = 1; i <= n - 1; i ++) {
        int u, v, w;
        std::cin >> u >> v >> w;
        V.push_back({w, u, v});
    }

    std::sort(V.begin(), V.end(), cmp);

    int ans = 1;
    for (int i = 0; i < V.size(); i ++) {
        ans = (ans * qpow((s - V[i][0] + 1), ((sz[find(V[i][1])] * sz[find(V[i][2])] - 1)))) % mod;
        join(V[i][1], V[i][2]);
    }

    std::cout << ans % mod << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t = 1;
    std::cin >> t;
    
    while (t--) {
        solve();
    }
    
    return 0;
}