原创 | 文 BFT机器人

01

摘要

迭代最近点（ICP）及其变式为此任务提供了简单且易于实现的迭代方法，但这些算法可能会收敛到虚假的局部最优值。

为了解决ICP通道中的局部最优和其他困难，我们提出了一种基于学习的方法，名为“深度最近点”（DCP），其灵感来自计算机视觉和自然语言处理的最新技术。我们的模型由三部分组成：点云特征提取网络、基于注意力的点云匹配预测，以及可微奇异值分解（SVD）层用来提取最终的刚性变换。

我们在 ModelNet40 数据集上端到端地训练我们的模型，并在多种设置中显示它比 ICP 及其变体（例如 Go-ICP、FGR）以及最近提出的基于学习的方法 PointNetLK 表现更好。除了提供最先进的配准技术之外，我们还评估了将学习到的特征转移到看不见的物体上的适用性。我们还对我们学习的模型进行初步分析，以帮助了解局部特征以及全局特征是否有利于点云配准。

02

本文的主要贡献

我们设计了一个子网络模块去解决ICP通道中的一些难点。并提出了一个简单的架构来预测对齐两个点云的刚性变换。评估多种环境下的效率和性能，并提供消融实验来验证我们的模块。另外，我们还分析局部特征还是全局特征对于配准更有用。以及我们发布代码以促进可重复性和未来的研究。

03

DCP（Deep Closest Point）网络结构

我们的模型由三个部分组成：

（1）我们将输入点云映射到网络中，这有助于识别匹配的点对（我们在这一步中比较了 PointNet和 DGCNN）。

（2）然后，结合指针网络的基于注意力的模块预测点云之间的软匹配。

（3）最后，可微奇异值分解层预测刚性变换。我们在 ModelNet40 上的各种设置中端到端地训练和测试我们的模型，表明我们的模型不仅高效，而且优于 ICP 及其扩展，以及最近提出的 PointNetLK 方法。我们学到的特征可以推广到看不见的数据，这表明我们的模型正在学习显着的几何特征。

DCP网络结构示意图如下所示：

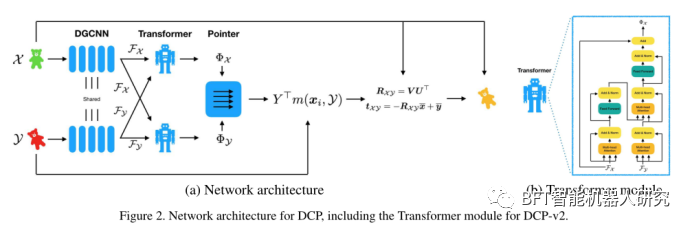
3.1特征提取模块

我们网络的第一阶段将未对齐的输入点云 X 和 Y 嵌入到一个公共空间中，用于查找两个点云之间的匹配点对。目的是找到一种方法，可以对刚性运动进行求商，同时保持对刚性匹配相关特征的敏感度。

我们评估了可学习嵌入模块的两种可能选择：PointNet 和 DGCNN]。由于我们使用两个输入点云的每点嵌入来生成映射 m 并恢复刚性变换，因此我们在输入点云中寻找每个点的特征，而不是每个点云的一个特征。因此，在这两个网络架构中，我们使用一个聚合函数生成最后的表示，记为 FX = {xL1 , xL2 , ..., xLi , ..., xLN } 和 FY = {yL1 , yL2 , ...., yLi , ..., yLN }，假设总共有 L 层。

PointNet 主要基于点云中每个点的嵌入来独立提取信息，而 DGCNN 明确地将局部几何特征合并到其表示中。特别是，给定一组点 X，DGCNN 构造一个k-NN 图G，对边缘端点处的值应用非线性以获得沿边值，并在每层中执行顶点聚合。

因此，DGCNN 的前向机制为

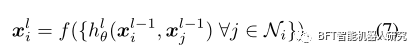
其中 Ni 表示图 G 中顶点 i 的临近值。由于不包含局部邻域信息，我们根据经验发现 DGCNN 的局部特征对于我们网络后续步骤中的高质量匹配至关重要。

3.2注意力机制模块

从 PointNet 过渡到 DGCNN 的原因是，我们观察到刚性对齐最有用的特征是从局部和全局特征中联合学习的，我们还可以通过使它们针对特定任务改进我们的匹配功能。即根据 X 和 Y 的特殊性一起更改特征，而不是独立嵌入 X 和 Y。受到最近 BERT 、非局部神经网络和关系网络基于注意力模型的成功的使用启发，我们设计了一个模块，通过捕获自注意力和条件注意力来学习上下文信息。

FX和FY为3.1中的模块生成的输出；这些输出是彼此独立计算的，我们的注意力模型学习一个函数，其中 P 是输出维度，它提供点云的新输出为

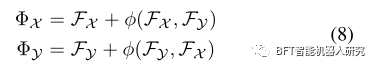
3.3指针生成模块（Pointer Generation）

当匹配估计 mk 远非最佳时，ICP 最常见的故障模式就会发生。当这种情况发生时，随后使用普通的ICP估计的刚性运动不会显着改善对准，从而导致虚假的局部最优。作为替代方案，我们学习的输出经过专门训练，以使用下面解释的简单过程来公开匹配的点对。我们将这个步骤称为“指针生成”，再次受到第 3.2 节介绍的注意力文献中术语的启发。

为了避免选择不可微的硬分配，我们使用一种概率方法来生成从一个点云到另一个点云的（单随机）“软映射”。

也就是说，每个 xi ∈ X 被分配一个 Y 元素上的概率向量，由下面公式给出

在这个公式里，表示注意力模块生成的 Y 的输出，Φxi 表示来自注意力模块的矩阵 ΦX 的第 i 行。我们可以将 m(xi, Y) 视为从每个 xi 到 Y 元素的“软指针”。

3.4 SVD模块

我们网络中的最后一个模块从第 3.3 节中计算的软匹配中提取刚性运动。我们使用软指针为 X 中的每个点生成 Y 中的匹配平均点：

为了通过网络反向传播梯度，我们需要对 SVD 进行微分。[29]描述了计算该导数的标准方法；此计算的版本包含在 PyTorch [30] 和 TensorFlow [1] 中。请注意，我们只需要解决 3 × 3 特征问题，这些问题足够小，可以使用简单的算法（原则上）甚至封闭式公式来解决。

3.5损失函数模块

组合起来，上面的模块从一对点云 X 和 Y 映射到刚性运动，使它们彼此对齐。初始特征模块（3.1）和注意力模块（3.2）均由一组神经网络权重参数化，这些权重必须在训练阶段学习。我们采用相当简单的训练策略，测量合成生成的点云对的与地面实况的偏差。

我们使用以下损失函数来衡量模型与真实刚性运动的一致性：

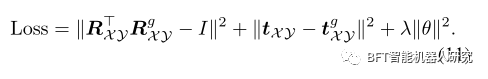
这里，g 表示真实值。前两项定义了 SE(3) 上的简单距离。第三项表示 DCP 参数 θ 的 Tikhonov 正则化，这有助于降低网络的复杂性。

04

消融实验

我们在本节中进行了几次消融实验，剖析 DCP 并用替代方案替换每个部分，以了解我们网络的价值。

4.1使用PointNet 还是 DGCNN？

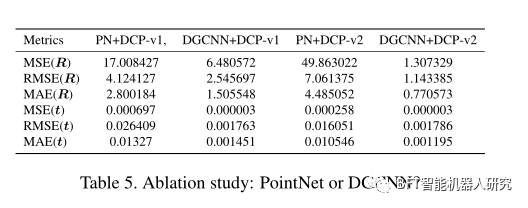
我们首先尝试回答 DGCNN 收集的局部特征是否比使用更简单的 PointNet 模型测量的粗略特征更有价值。正如[50]中所讨论的，PointNet 学习整个形状的全局描述符，而DGCNN 通过构建k-NN图来学习局部几何特征。我们用 PointNet（表示为 PN）替换 DGCNN，并使用 DCP-v1 和 DCP-v2 在 ModelNet40 上进行实验。表 5. 使用 DGCNN 的模型始终优于使用 PointNet 的模型。

4.2是MLP还是SVD效果好

虽然 MLP 原则上是通用逼近器，但我们的 SVD 层旨在专门计算刚性运动。在这个实验中，我们检查 MLP 还是SVD层是否更适合配准。我们在 ModelNet40 上将 MLP 和 SVD 与 DCP-v1 和 DCP-v2 进行比较。

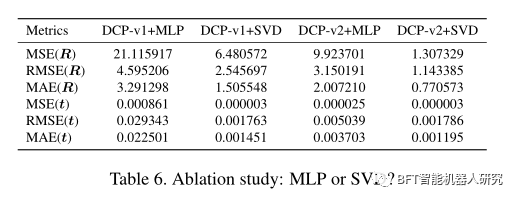
表 6 显示 DCP-v1 和 DCP-v2 在 SVD 层上的表现都比 MLP 更好。这支持了我们使用 SVD 计算刚性变换的动机。

05

结论

从某种意义上说，我们的“深度最近点”技术的关键观察是，学习到的特征极大地促进了刚性对齐算法；通过结合 DGCNN [50] 和注意力模块，我们的模型可靠地提取找到对齐两个输入点云的刚性运动所需的对应关系。我们的端到端可训练模型足够可靠，可以在单次传递中提取高质量的对齐，这可以通过经典 ICP 的迭代或“抛光”来改进。

DCP 可立即应用于刚性对准问题，作为 ICP 的直接替代品，并具有改进的性能。除了直接使用之外，我们的实验还为未来的探究提出了几种途径。一个简单的扩展是看看我们学习的输出是否转移到其他任务，如分类和分割。我们还可以训练 DCP 以迭代（或递归）方式应用来优化对齐，而不是尝试在单次传递中进行对齐；强化学习的洞察力可以帮助改进这个方向的方法，使用均方误差作为奖励来学习控制何时停止迭代的策略。

我们还对场景测试感兴趣，这些场景通常有高达 300,000 个点。然而，当前的深度网络只能处理对象级点云（每个点云通常有大约 500 到 5,000 个点）；这是最近点云学习方法的常见局限性。无论什么任务，场景测试都需要设计一个高效的场景级点云编码网络，这对于点云学习来说是一个有前途但具有挑战性的方向。

最后，我们希望我们的方法可以合并到更大的网络中，以实现高精度同步定位和建图（SLAM）或运动结构（SFM）。

作者 | 江城

排版 | 居居手

更多精彩内容请关注公众号：BFT机器人

本文为原创文章，版权归BFT机器人所有，如需转载请与我们联系。若您对该文章内容有任何疑问，请与我们联系，将及时回应。