学习来源
【自制】01背包问题算法动画讲解_哔哩哔哩_bilibili
问题描述
有N件物品,第i件物品的重量是w[i],价值是p[i]。
有一个背包,背包的承重是W。
求解:将哪些物品装入背包可获得最大价值。
实例说明
有如下物品,给定每件物品的重量和价值:
| 物品 | 重量 | 价值 |
| 葡萄 | 2 | 3 |
| 矿泉水 | 3 | 5 |
| 西瓜 | 4 | 6 |
有一个背包,承重是6。
请求出背包放入物品的最大价值。
01背包解题思路
01背包是基于动态规划解题的。
即将对承重6的背包的装载最大价值问题的求解,分解为对更小承重的背包的装载最大价值问题的求解。当分解到背包承重只有0时,就可以轻易得到背包装载最大价值为0。
同时,我们还需对物品的选择进行分解,将对多种物品的选择,分解更少种物品的选择,直到选择物品为0时,无论什么背包的装载最大价值都是0。
因此,我们可以得到一个二维矩阵图如下:
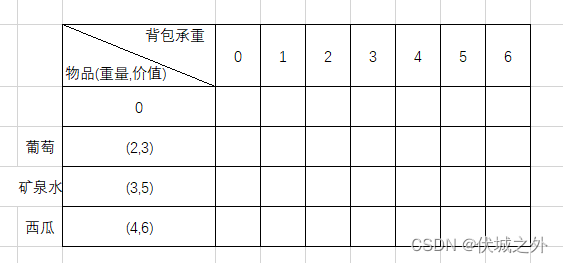
其中:
- 第0列表示背包承重为0,此时装不了任何物品,因此此背包的装载最大价值都为0。
- 第0行表示背包不选择任何物品放入,因此无论什么背包,装载价值都为0。
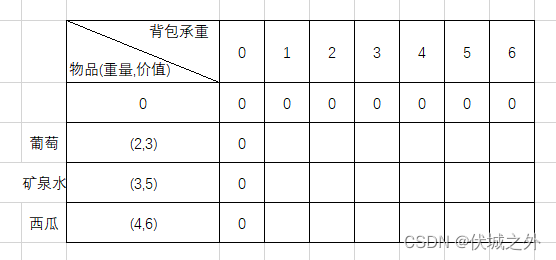
我们可以用dp二维数组来表示,行用i变量表示,列用j变量表示,因此:
- dp[i][0] = 0
- dp[0][j] = 0
而dp[i][j]表示的含义是:背包承重为 j 的时候,选择物品范围 0~i 时,可以产生的最大价值。
下面我们讨论:背包承重为1时,只选0~1范围的物品,所能产生的最大价值,即求解dp[1][1],如下图标黄处所示
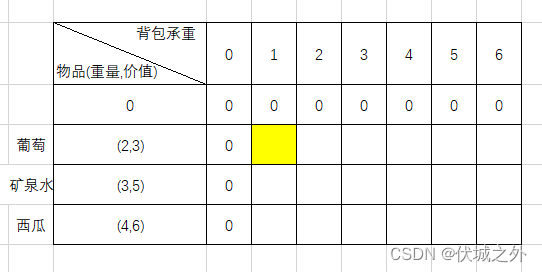
此时,我们有两种选择:
- 不选择第1行物品(即葡萄),只选择前面的物品,此时相当于 dp[1][1] = dp[0][1]
- 选择第1行物品(即葡萄),但是由于葡萄重量为2 > 背包承重1,因此选不了,因此还是相当于 dp[1][1] = dp[0][1]
最终dp[1][1] = dp[0][1],
此时似乎还看不出状态转移方程,我们继续往后推导
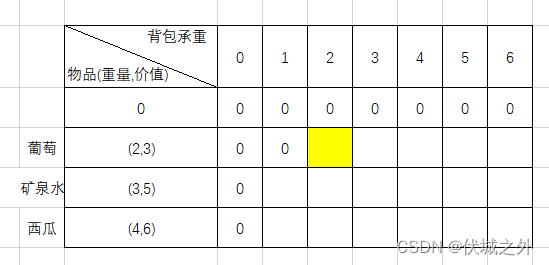
接下来,我们扩大背包承重,即背包承重为2,此时依旧两种选择:
- 不选择第1行物品(即葡萄),只选择前面的物品,此时相当于 dp[1][2] = dp[0][2]
- 选择第1行物品(即葡萄),但是由于葡萄重量为2 = 背包承重2,因此可以选。接下来就是关键点了,背包装了葡萄后,还剩下0承重,那么0承重可以装什么呢?请看下面绿色标记

我们发现,背包承重0时,不选葡萄的话(因为葡萄已经装入背包了,现在在讨论剩余承重的最大价值) 的最大价值是0。
因此,选了背包承重2,选了葡萄后能产生的最大价值为 3 + dp[0][0] = 3 + 0 = 3
而前面背包承重2,不选葡萄后能产生的最大价值继承自dp[0][2] = 0,
因此我们肯定选择装入葡萄,产生最大价值3。
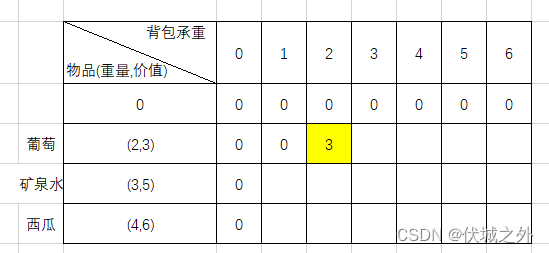
之后同理:背包承重3
如果不装葡萄,则最大价值继承自dp[0][3] = 0,
如果装入葡萄的话,葡萄产生价值3,剩余背包承重1,不选葡萄,能产生的最大价值为dp[0][1] = 0,因此装入葡萄的最大价值为3+0 = 3,
对比来看,背包承重3,装入葡萄产生的价值最大为3。
之后同理退出:背包承重4,5,6是否装入葡萄的最大价值
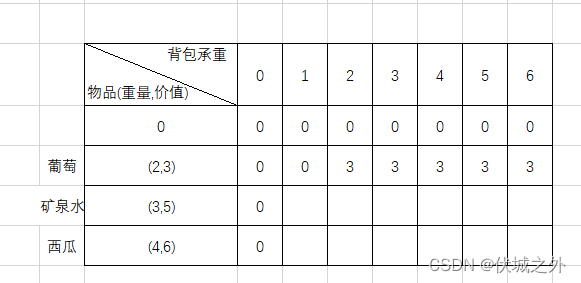
下面继续扩大物品的选择,将矿泉水纳入选择范围,然后继续从背包承重1开始讨论:
背包承重1:
如果不选择矿泉水,那么产生的最大价值,继承自dp[1][1] = 0
如果选择矿泉水,则因为承重不够,装不了,因此也继承dp[1][1] = 0
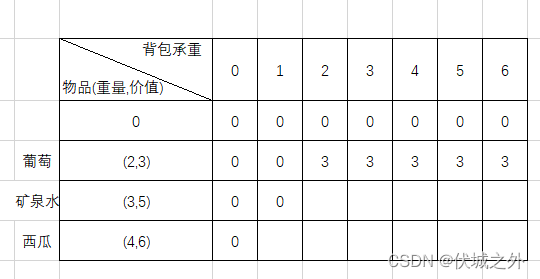
背包承重2:
如果不选择矿泉水,那么产生最大价值,继承自dp[1][2] = 3
如果选择矿泉水,则因为承重不够,装不了,因此也继承dp[1][2] = 3
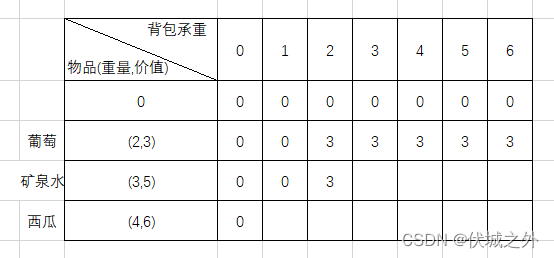
背包承重3:
如果不选择矿泉水,那么产生最大价值,继承自dp[1][3] = 3
如果选择矿泉水,则承重刚好,矿泉水价值5纳入,剩余承重0,选择不含矿泉水的物品的最大价值为dp[1][0] = 0,因此最后价值为 5 + 0 = 5
对比来看,选择矿泉水的最大价值更大。
背包承重4同理。
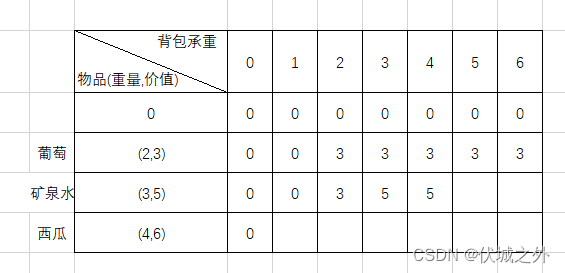
我们来看看背包承重5:
如果不选择矿泉水,那么最大价值继承自dp[1][5] = 3
如果选择矿泉水,那么纳入矿泉水价值5,还剩余2承重,而2承重,不选矿泉水对应的最大价值为dp[1][2] = 3,因此总价值为8
对比来看,选择矿泉水的价值最大
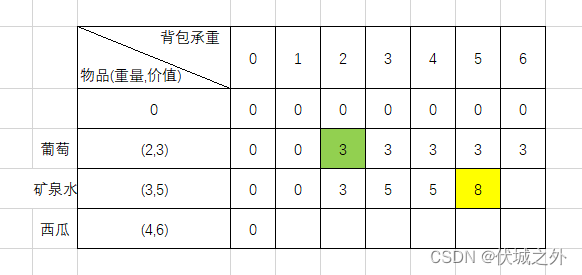
按此规则可以推导处后面所有dp
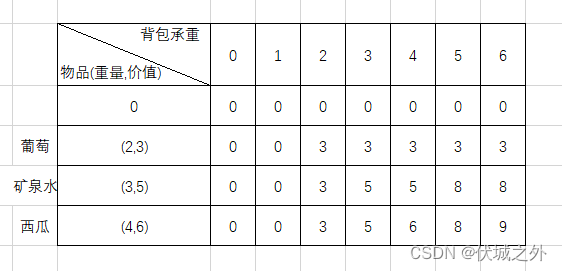
状态转移方程
首先 dp[i][j] 表示:承重为 j 的背包,选择 0~i 范围的物品装入的最大价值。
其中 dp[i][0] = 0,dp[0][j] = 0
如果 i !== 0 && j !== 0,则
dp[i][j] = Math.max(dp[i-1][j], p[i] + dp[i-1][j - w[i]] )
状态转移方程中
- dp[i-1][j] 表示 不选择物品 i 能产生的最大价值
- p[i] + dp[i-1][j - w[i]] 表示 选择物品 i 后纳入了物品 i 的价值p[i],剩余承重为 j - w[i],其中w[i]是物品 i 的重量,而由于我们已经选择了物品 i ,因此剩余承重 j - w[i] 只能选择0~i-1范围物品,对应的最大价值为 dp[i-1][j - w[i]]
当然有一个优化动作就是:
如果背包承重放不下物品 i ,则该承重背包,只能从 0~i-1范围内选择商品,即直接继承dp[i-1][j]。
因此完整的状态转移方程为:
dp[i][0] = 0,
dp[0][j] = 0,
if(w[i] <= W) {
dp[i][j] = Math.max(dp[i-1][j], p[i] + dp[i-1][j - w[i]] )
} else {
dp[i][j] = dp[i-1][j]
}