前言：以2015年发表在期刊《MATHEMATICAL GAME THEORY AND APPLICATIONS》上的文章《Strong Coalitional Equilibrium in a Transportation Game》为学习资料，学习关于车辆路径模型的合作博弈。以下是本人对文献内容的一些粗浅理解，由于本人英文阅读水平有限，可能对文献理解的不到位，对VRP合作博弈问题感兴趣的人员可以下载文献进一步学习。

1. 文献研究回顾

文献研究的背景：合作博弈理论研究协作行为的能力，为了减少不同承运人之间的运输成本。车辆路径模式方面的合作还只有少数文献研究。文献[3-5]运用合作博弈的理论研究合作问题。在合作博弈理论中最重要的目标是博弈的特征函数，博弈的特征函数可以用来评估参与者构建联盟能获得的总成本。实际合作的数学模型的主要作用是选择一个构造方法去建立上面提及的博弈的特征函数。由于该问题的高纬度，去评估合作路径博弈特征函数的计算复杂度增加了。由于这个原因，本文不能用精确解算法去求解少量客户的路径问题，如文献[2-4]。同时，一般的启发式方法也不能保证求出问题的结果后得到的特征函数满足次可加性。至今，特征函数的次可加性对于合作后产生的成本节约是重要的。当考虑动态合作模型时，运用Petrosjan倡导的归罪分配方法（imputation distribution procedures），以及Petrosjan和Zenkevich出版的书[1]中提到的稳定合作理论。

文献主要研究问题如下：承运人在大规模的运输网络进行合作的条件下，本文研究车辆路径问题的运输成本最小化。本文所建模型是带有可转让效用函数的动态合作博弈模型。提出一个启发式的迭代算法用于构建静态博弈中的带有次可加性的函数。调整算法去构造动态路径博弈问题中的特征函数。运用Shapley值和核心法去形成最优的解。最后，动态博弈中我们描述一个成本分配的过程，保证核心的时间一致性和合作协议的动态稳定性。

文献研究的主要成果：在承运人合作条件下特征函数的确定方法，特征函数要满足次可加性。为了求解该问题，我们提出被称之为联盟归纳算法。该算法结合了好几种求解高维问题的启发式算法。
计算特征函数评价值的算法产生了有效的货物运输路线。因此，我们得到了每个合作者的直接成本、联盟的总成本和运用Shapley值求出的成本分配。这些信息决定了承运人在博弈中的合作行为。通过借助联盟归纳算法分析承运人在动态模型中的合作，我们引进了迭代联盟归纳算法。迭代联盟归纳算法的应用保证了每个子博弈中特征函数的次可加性。核心最优化理论和提出的成本分配方法保证了分配过程有较强的动态稳定性。而且，个体参与者的偏差和他们形成的联盟在任何阶段都不是合理的，直到联盟成本没有减少为止。

以下仅就车辆路径问题的静态博弈模型发表下本人对文献的理解，不涉及动态运输博弈模型。

2. 问题描述

假设运输服务市场上有好几家运输公司或者叫做承运人。每个承运人有自己的顾客集合和资源（仓库和车辆）。这些承运人考虑组建不同的联盟去减少他们各自的运输成本。不同的联盟都满足可以利用共享的资源去进行运输服务的条件。因此，在合作的框架下，每个联盟中的成员重新分配各自服务的顾客。很明显这种重新分配顾客的方式调整了每个联盟中成员的车辆运输路径。在共享车辆的联合路径合作模式下，决策者面临在时间不充分的情况下需要尽快分配路线以使联盟总运输成本最小的问题，这个问题是一个NP难问题。

在联盟的最优路线确定下来之后，然后在计算联盟的总运输成本，这是可能去计算合作路径博弈的特征函数的。只要博弈的特征函数满足次可加性，参与者就愿意组建联盟。一般而言，用启发式算法去求联盟总运输成本最小化不能保证满足这一性质。因此，车辆路径问题要求提出特别的元启发式算法求解路线设计问题得到最优解或近似最优解，确保特征函数满足次可加性。

车辆路径问题的难点是构建车辆的运行路径以满足顾客的运输需求。根据实际情况，每条路线的起点和终点都是同一个仓库。对于每一条路线，要求车辆在仓库的状态是不进行任何装卸活动的。换句话说，车辆只能在路线上使用，仓库只是作为存放车辆的一个场所。每个顾客点只被服务一次。而且，每条路线上总的顾客需求不能超过该车辆的最大容量。每辆车移动到顾客点的时间加上在顾客点服务的时间不能超过一个给定的数值。带有时间窗的路径问题中，顾客被服务的时间必须要在给定的时间范围内。通常这类问题旨在优化使总的路线长度最短。但是在很多情况下使用的车辆数量不是固定的，为了使总运输成本最低，很明显也要求去减少车辆的使用数量。这么说的一个潜在原因是向第三方进行车辆维修的成本或是租赁车辆的成本明显超出了从最短路径上取得的收益，这种情况只是与承运人使用自己的车辆进行运输的情况相比而言的。

3. 静态合作路径博弈的数学模型

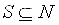令是在相同运输网络上的承运人集合。是参与人可以加入的联盟，我们研究的是可转移支付的静态博弈。联盟的成本是由两部分组成的，车辆的维护成本和运输成本。假设车辆的运输成本与该车辆运行的总路线长度是线性关系。联盟中车辆的维护成本是固定的并且每辆车的维护成本都是相同的。因此，问题的成本函数如下：

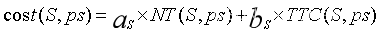
假定每个承运人只有一个仓库，并且合作的承运人之间能够借助一个特定的支付过程重新分配运输成本。

考虑合作路径博弈特征函数的结构，要求必须满足次可加性。在联盟的可行路线集合条件下，研究下面的成本最小化问题。

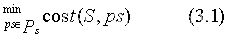
（要求在条件下联盟总运输成本最小）

令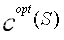是公式（3.1）求得的最小值。我们强调在顾客数量较多时，问题的求解用到启发式算法。因此，启发式算法求得的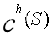值要至少大于等于精确值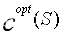，即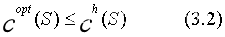
。

首先找到所有单个联盟的特征函数值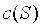，然后找到所有由两个成员构成的联盟的特征函数值，逐步增加联盟的规模直到评估总联盟的特征函数值。由公式（3.5），不等式（3.2）和（3.4）可知，所构建的特征函数具有次可加性：

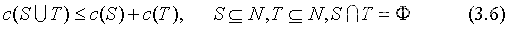
计算可转移支付的路径博弈特征函数的算法叫做直接联盟归纳算法（the direct coalition induction algorithm）。因此，进行如下定义。

定理：可转移支付合作静态路径博弈的特征函数由直接联盟归纳算法在满足公式（3.6）的条件下产生。

考虑 D0、D1、D2 和 D3 这四个承运人之间的合作，他们分别拥有54、49、44、53个顾客。每个顾客在运输网络中只有一个订单需要在给定的节点之间进行运输。假设运输节点距离矩阵是给定的，距离矩阵中的数值是非负数。因此，在四个承运人达成合作的情况下，承运人需要服务的顾客数是200个。假定每个承运人在该地区服务的顾客数是均匀分配的，而且，承运人为顾客服务的时间窗是宽松的，这就保证了可以配置少量的车辆，但是这增加了问题的计算复杂度。车辆高的载重量与顾客的需求相比较也促进了更少车辆的使用。车辆的维护成本是5000元，单位路线的成本是5元。为了求解该问题，我们运用Ropke算法[6]。作为一个原始的设置，Ropke算法考虑更为一般性的问题，我们研究的问题是它的特例。为了使用该算法去有效的找到运输路径，使用模拟退火算法去联合好几种基本的启发式算法，这样可以更快的构造新的解。这些启发式算法中的某几种算法能从解中消除顾客，其他的算法能再一次把消除的顾客添加到解里面。每次迭代选择哪两种具体的基本启发式算法取决于求解过程中得到的解的质量。为了使搜索变化的更快，目标函数的精确值用目标函数的干扰值取代。对于每一个联盟，表1展示了由直接联盟归纳算法求出的成本最小化问题的最优解和博弈的特征函数值。

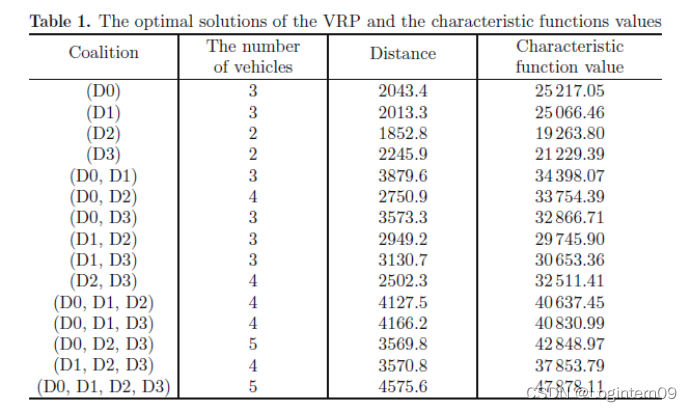
由表1可知，所有承运人在没有合作之前总的最小运输成本一共是90776.70元。在合作之后，总的运输成本是47878.11元。由这个算例可得在合作之后所有承运人的成本节约了大概47%。

运用Shapley值计算合作博弈的成本分配，得出与没有合作时的最小成本相比较每个承运人都可以得到一个相当可观的成本减少，见表2.

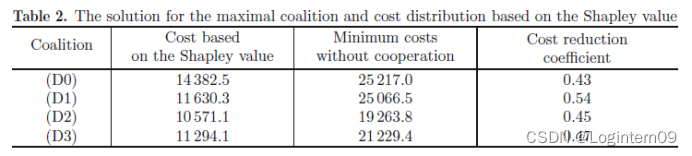
对于一个承运人来说，运用Shapley值进行成本分配所得到的成本减少的变化范围是43%-54%。

参考文献

[1] Petrosjan, L.A. and Zenkevich, N.A., Principles of Stable Cooperation, Mat. Teor. Igr Pril., 2009, vol. 1,no. 1, pp. 106–123.
[2] Baldacci, R., Mingozzi, A., and Roberti, R., Recent Exact Algorithms for Solving the Vehicle Routing Problem under Capacity and Time Window Constraints, Eur. J. Operat. Res., 2012, vol. 218, pp. 1–6.
[3] Ergun, O., Kuyzu, G., and Savelsbergh, M.W.P., Shipper Collaboration, ¨ Comput. Operat. Res., 2007,vol. 34, pp. 1551–1560.
[4] Kallehauge, B., Formulations and Exact Algorithms for the Vehicle Routing Problem with Time Windows, Comput. Operat. Res., 2008, vol. 35, pp. 2307–2330.
[5] Krajewska, M.A., Kopfer, H., Laporte, G., Ropke, S., and Zaccour, G., Horizontal Cooperation
among Freight Carriers: Request Allocation and Profit Sharing, J. Operat. Res. Soc., 2008, vol. 59,pp. 1483–1491.
[6] Ropke, S. and Pisinger, D., An Adaptive Large Neighborhood Search Heuristic for the Pickup and Delivery Problem with Time Windows, Transport. Sci., 2006, vol. 40, pp. 455–472.
[7] Zakharov, V. and Dementieva, M., Multistage Cooperative Games and Problem of Time-Consistency,Int. Game Theory Rev., 2004, vol. 6, no. 1, pp. 1–14.
[8] Zakharov, V. and Kwon, O-Hun, Selectors of the Core and Consistency Properties, Game Theory Appl.,1999, vol. 4, pp. 237–250.