描述

小乐乐上课需要走n阶台阶，因为他腿比较长，所以每次可以选择走一阶或者走两阶，那么他一共有多少种走法？

输入描述

输入包含一个整数n (1 ≤ n ≤ 30)

输出描述

输出一个整数，即小乐乐可以走的方法数。

思路：（采用递归的思想）

1.如果只有1级台阶，那么就只有1种跳法。

2.如果有2级台阶，那么就有两种跳法，一次跳一级或者一次跳两级。

3.如果台阶级数大于2，设为n的话，这时我们把n级台阶的跳法看成n的函数，记为f(n),第一次跳的时候有两种选择：一是第一次跳一级，此时跳法的数目等于后面剩下n-1级台阶的跳法数目，即f（n-1），二是第一次跳两级，此时跳法的数目等于后面剩下n-2级台阶的跳法数目，即f（n-2），因此n级台阶的不同跳法数目的总数为f（n）=f(n-1)+f(n-2),不难看出就是斐波那契数列。

 

 

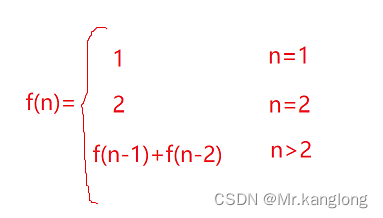
#include <stdio.h>
int fib(int n)
{
    if(n==1)
        return 1;
    if(n==2)
        return 2;
    return fib(n-1)+fib(n-2);

}
int main()
{
    int n=0;
    scanf("%d",&n);
    int ret = fib(n);
    printf("%d",ret);
    return 0;
}