什么是哈希算法

哈希算法的定义和原理非常简单，基本上一句话就可以概括了。将任意长度的二进制值串映射为固定长度的二进制值串，这个映射的规则就是哈希算法，而通过原始数据映射之后得到的二进制值串就是哈希值。但是，要想设计一个优秀的哈希算法并不容易，至少需要满足的几点要求：

从哈希值不能反向推导出原始数据（所以哈希算法也叫单向哈希算法）；
对输入数据非常敏感，哪怕原始数据只修改了一个 Bit，最后得到的哈希值也大不相同；
散列冲突的概率要很小，对于不同的原始数据，哈希值相同的概率非常小；
哈希算法的执行效率要尽量高效，针对较长的文本，也能快速地计算出哈希值。

哈希算法的应用

哈希算法的应用非常非常多，我选了最常见的七个，分别是安全加密、唯一标识、数据校验、散列函数、负载均衡、数据分片、分布式存储。

安全加密

说到哈希算法的应用，最先想到的应该就是安全加密。最常用于加密的哈希算法是 MD5（MD5 Message-Digest Algorithm，MD5 消息摘要算法）和 SHA（Secure Hash Algorithm，安全散列算法）。

除了这两个之外，当然还有很多其他加密算法，比如 DES（Data Encryption Standard，数据加密标准）、AES（Advanced Encryption Standard，高级加密标准）。

对用于加密的哈希算法来说，有两点格外重要。第一点是很难根据哈希值反向推导出原始数据，第二点是散列冲突的概率要很小。

第一点很好理解，加密的目的就是防止原始数据泄露，所以很难通过哈希值反向推导原始数据，这是一个最基本的要求。所以我着重讲一下第二点。实际上，不管是什么哈希算法，我们只能尽量减少碰撞冲突的概率，理论上是没办法做到完全不冲突的。为什么这么说呢？

这里就基于组合数学中一个非常基础的理论，鸽巢原理（也叫抽屉原理）。这个原理本身很简单，它是说，如果有 10 个鸽巢，有 11 只鸽子，那肯定有 1 个鸽巢中的鸽子数量多于 1 个，换句话说就是，肯定有 2 只鸽子在 1 个鸽巢内。

我们知道，哈希算法产生的哈希值的长度是固定且有限的。比如前面举的 MD5 的例子，哈希值是固定的 128 位二进制串，能表示的数据是有限的，最多能表示 2¹²⁸ 个数据，而我们要哈希的数据是无穷的。基于鸽巢原理，如果我们对 2¹²⁸+1 个数据求哈希值，就必然会存在哈希值相同的情况。这里你应该能想到，一般情况下，哈希值越长的哈希算法，散列冲突的概率越低。

不过，即便哈希算法存在散列冲突的情况，但是因为哈希值的范围很大，冲突的概率极低，所以相对来说还是很难破解的。像 MD5，有 2¹²⁸ 个不同的哈希值，这个数据已经是一个天文数字了，所以散列冲突的概率要小于 1/2¹²⁸。

如果我们拿到一个 MD5 哈希值，希望通过毫无规律的穷举的方法，找到跟这个 MD5 值相同的另一个数据，那耗费的时间应该是个天文数字。所以，即便哈希算法存在冲突，但是在有限的时间和资源下，哈希算法还是很难被破解的。

除此之外，没有绝对安全的加密。越复杂、越难破解的加密算法，需要的计算时间也越长。比如 SHA-256 比 SHA-1 要更复杂、更安全，相应的计算时间就会比较长。密码学界也一直致力于找到一种快速并且很难被破解的哈希算法。我们在实际的开发过程中，也需要权衡破解难度和计算时间，来决定究竟使用哪种加密算法。

唯一标识

如果要在海量的图库中，搜索一张图是否存在，我们不能单纯地用图片的元信息（比如图片名称）来比对，因为有可能存在名称相同但图片内容不同，或者名称不同图片内容相同的情况。那我们该如何搜索呢？

我们知道，任何文件在计算中都可以表示成二进制码串，所以，比较笨的办法就是，拿要查找的图片的二进制码串与图库中所有图片的二进制码串一一比对。如果相同，则说明图片在图库中存在。但是，每个图片小则几十 KB、大则几 MB，转化成二进制是一个非常长的串，比对起来非常耗时。有没有比较快的方法呢？

我们可以给每一个图片取一个唯一标识，或者说信息摘要。比如，我们可以从图片的二进制码串开头取 100 个字节，从中间取 100 个字节，从最后再取 100 个字节，然后将这 300 个字节放到一块，通过哈希算法（比如 MD5），得到一个哈希字符串，用它作为图片的唯一标识。通过这个唯一标识来判定图片是否在图库中，这样就可以减少很多工作量。

如果还想继续提高效率，我们可以把每个图片的唯一标识，和相应的图片文件在图库中的路径信息，都存储在散列表中。当要查看某个图片是不是在图库中的时候，我们先通过哈希算法对这个图片取唯一标识，然后在散列表中查找是否存在这个唯一标识。

如果不存在，那就说明这个图片不在图库中；如果存在，我们再通过散列表中存储的文件路径，获取到这个已经存在的图片，跟现在要插入的图片做全量的比对，看是否完全一样。如果一样，就说明已经存在；如果不一样，说明两张图片尽管唯一标识相同，但是并不是相同的图片。

数据校验

电驴这样的 BT 下载软件你肯定用过吧？我们知道，BT 下载的原理是基于 P2P 协议的。我们从多个机器上并行下载一个 2GB 的电影，这个电影文件可能会被分割成很多文件块（比如可以分成 100 块，每块大约 20MB）。等所有的文件块都下载完成之后，再组装成一个完整的电影文件就行了。

我们知道，网络传输是不安全的，下载的文件块有可能是被宿主机器恶意修改过的，又或者下载过程中出现了错误，所以下载的文件块可能不是完整的。如果我们没有能力检测这种恶意修改或者文件下载出错，就会导致最终合并后的电影无法观看，甚至导致电脑中毒。现在的问题是，如何来校验文件块的安全、正确、完整呢？

具体的 BT 协议很复杂，校验方法也有很多，我来说其中的一种思路。

我们通过哈希算法，对 100 个文件块分别取哈希值，并且保存在种子文件中。我们在前面讲过，哈希算法有一个特点，对数据很敏感。只要文件块的内容有一丁点儿的改变，最后计算出的哈希值就会完全不同。所以，当文件块下载完成之后，我们可以通过相同的哈希算法，对下载好的文件块逐一求哈希值，然后跟种子文件中保存的哈希值比对。如果不同，说明这个文件块不完整或者被篡改了，需要再重新从其他宿主机器上下载这个文件块。

散列函数

散列函数是设计一个散列表的关键。它直接决定了散列冲突的概率和散列表的性能。不过，相对哈希算法的其他应用，散列函数对于散列算法冲突的要求要低很多。即便出现个别散列冲突，只要不是过于严重，我们都可以通过开放寻址法或者链表法解决。

不仅如此，散列函数对于散列算法计算得到的值，是否能反向解密也并不关心。散列函数中用到的散列算法，更加关注散列后的值是否能平均分布，也就是，一组数据是否能均匀地散列在各个槽中。除此之外，散列函数执行的快慢，也会影响散列表的性能，所以，散列函数用的散列算法一般都比较简单，比较追求效率。

负载均衡

我们知道，负载均衡算法有很多，比如轮询、随机、加权轮询等。那如何才能实现一个会话粘滞（session sticky）的负载均衡算法呢？也就是说，我们需要在同一个客户端上，在一次会话中的所有请求都路由到同一个服务器上。

最直接的方法就是，维护一张映射关系表，这张表的内容是客户端 IP 地址或者会话 ID 与服务器编号的映射关系。客户端发出的每次请求，都要先在映射表中查找应该路由到的服务器编号，然后再请求编号对应的服务器。这种方法简单直观，但也有几个弊端：

如果客户端很多，映射表可能会很大，比较浪费内存空间；
客户端下线、上线，服务器扩容、缩容都会导致映射失效，这样维护映射表的成本就会很大；

如果借助哈希算法，这些问题都可以非常完美地解决。我们可以通过哈希算法，对客户端 IP 地址或者会话 ID 计算哈希值，将取得的哈希值与服务器列表的大小进行取模运算，最终得到的值就是应该被路由到的服务器编号。这样，我们就可以把同一个 IP 过来的所有请求，都路由到同一个后端服务器上。

数据分片

假如我们有 1T 的日志文件，这里面记录了用户的搜索关键词，我们想要快速统计出每个关键词被搜索的次数，该怎么做呢？

我们来分析一下。这个问题有两个难点，第一个是搜索日志很大，没办法放到一台机器的内存中。第二个难点是，如果只用一台机器来处理这么巨大的数据，处理时间会很长。

针对这两个难点，我们可以先对数据进行分片，然后采用多台机器处理的方法，来提高处理速度。具体的思路是这样的：为了提高处理的速度，我们用 n 台机器并行处理。我们从搜索记录的日志文件中，依次读出每个搜索关键词，并且通过哈希函数计算哈希值，然后再跟 n 取模，最终得到的值，就是应该被分配到的机器编号。

这样，哈希值相同的搜索关键词就被分配到了同一个机器上。也就是说，同一个搜索关键词会被分配到同一个机器上。每个机器会分别计算关键词出现的次数，最后合并起来就是最终的结果。

分布式存储

现在互联网面对的都是海量的数据、海量的用户。我们为了提高数据的读取、写入能力，一般都采用分布式的方式来存储数据，比如分布式缓存。我们有海量的数据需要缓存，所以一个缓存机器肯定是不够的。于是，我们就需要将数据分布在多台机器上。

该如何决定将哪个数据放到哪个机器上呢？我们可以借用前面数据分片的思想，即通过哈希算法对数据取哈希值，然后对机器个数取模，这个最终值就是应该存储的缓存机器编号。

但是，如果数据增多，原来的 10 个机器已经无法承受了，我们就需要扩容了，比如扩到 11 个机器，这时候麻烦就来了。因为，这里并不是简单地加个机器就可以了。

原来的数据是通过与 10 来取模的。比如 13 这个数据，存储在编号为 3 这台机器上。但是新加了一台机器中，我们对数据按照 11 取模，原来 13 这个数据就被分配到 2 号这台机器上了。

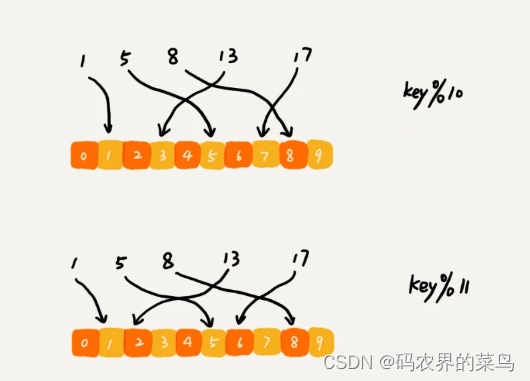
在这里插入图片描述
因此，所有的数据都要重新计算哈希值，然后重新搬移到正确的机器上。这样就相当于，缓存中的数据一下子就都失效了。所有的数据请求都会穿透缓存，直接去请求数据库。这样就可能发生雪崩效应，压垮数据库。

所以，我们需要一种方法，使得在新加入一个机器后，并不需要做大量的数据搬移。这时候，一致性哈希算法就要登场了。

假设我们有 k 个机器，数据的哈希值的范围是[0, MAX]。我们将整个范围划分成 m 个小区间（m 远大于 k），每个机器负责 m/k 个小区间。当有新机器加入的时候，我们就将某几个小区间的数据，从原来的机器中搬移到新的机器中。这样，既不用全部重新哈希、搬移数据，也保持了各个机器上数据数量的均衡。

一致性哈希算法的基本思想就是这么简单。除此之外，它还会借助一个虚拟的环和虚拟结点，更加优美地实现出来。