C数据结构与算法——常见排序算法时间复杂度比较 应用

news2024/10/6 16:20:49

实验任务

(1) 掌握常见比较排序算法的实现；
(2) 掌握常用比较排序算法的性能及其适用场合。

实验内容

(1) 平均时间复杂度O(n2)和O(nlog2n)的算法至少各选两种实现；
(2) 待排序的无重复关键字存放在一维整型数组中，数量为60000个；
(3) 对于不同的排序算法，分成两轮进行性能对比：
     第1轮对比：关键字初始为升序状态；
     第2轮对比：关键字初始为乱序状态；

实验源码

// 由于临近期末，所以插入排序和快速排序不加以验证（读者自行验证）

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <profileapi.h>

#define LENGTH(arr) (sizeof(arr)/sizeof((arr)[0])) // 计算数组长度

void PrintCompare(int arr[], int length); // 打印排序结果
void knuthShuffle(int arr[], int length); // 洗牌算法
void swapInt(int *card_1, int *card_2); // 交换函数
double BubbleSortTimes(int arr[], int length); // 冒泡排序测时
double SelectSortTimes(int arr[], int length); // 选择排序测时
double HeapSortTimes(int arr[], int length); // 堆排序测时
void adjustHeap(int arr[], int i, int length); // 堆排序核心部分(大小堆顶)
double MergeSortTimes(int arr[], int length); // 归并排序测时
void mergeSort(int arr[], int left, int right, int temp[]); // 归分
void merge(int arr[], int left, int mid, int right, int temp[]); // 分治

int main() {

    srand(time(NULL)); // 初始化随机种子
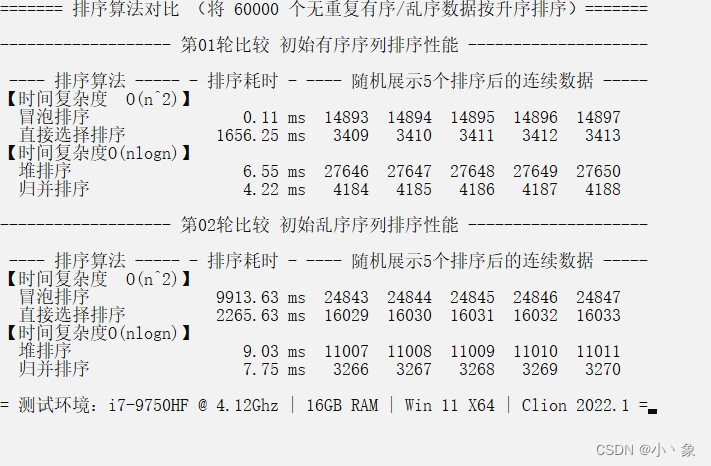
    printf("======= 排序算法对比 （将 60000 个无重复有序/乱序数据按升序排序）=======\n");
    printf("\n");
    printf("------------------- 第01轮比较 初始有序序列排序性能 --------------------\n");
    int arr[60000];
    // 有序数组
    for (int i = 0; i < LENGTH(arr); i++) { // 一副有序牌
        arr[i] = i + 1;
    }
    PrintCompare(arr, LENGTH(arr));
    printf("\n");
    printf("------------------- 第02轮比较 初始乱序序列排序性能 --------------------\n");
    // 无序数组
    knuthShuffle(arr, LENGTH(arr)); // 洗牌打乱顺序
    PrintCompare(arr, LENGTH(arr));

    printf("\n= 测试环境：i7-9750HF @ 4.12Ghz | 16GB RAM | Win 11 X64 | Clion 2022.1 =");

    getchar();
}

void PrintCompare(int arr[], int length) {
    int tempArr[length];
    printf("\n ---- 排序算法 ----- - 排序耗时 - ---- 随机展示5个排序后的连续数据 -----\n");
    printf("【时间复杂度  O(n^2)】\n");

    for (int i = 0; i < length; i++) {
        tempArr[i] = arr[i];
    }
    printf("  冒泡排序\t\t%7.2lf ms", BubbleSortTimes(tempArr, length));
    int randIndex = rand() % length; // 0 - (length-1)
    int printNum = 5;
    for (int i = 0; i < printNum; i++) {
        if (tempArr[randIndex] >= (length - printNum)) {
            i = 0;
        } else {
            printf("%7d", tempArr[randIndex++]);
        }
    }
    printf("\n");

    for (int i = 0; i < length; i++) {
        tempArr[i] = arr[i];
    }
    printf("  直接选择排序\t\t%7.2lf ms", SelectSortTimes(tempArr, length));
    randIndex = rand() % length; // 0 - (length-1)
    printNum = 5;
    for (int i = 0; i < printNum; i++) {
        if (tempArr[randIndex] >= (length - printNum)) {
            i = 0;
        } else {
            printf("%7d", tempArr[randIndex++]);
        }
    }
    printf("\n");


    printf("【时间复杂度O(nlogn)】\n");

    for (int i = 0; i < length; i++) {
        tempArr[i] = arr[i];
    }
    printf("  堆排序\t\t%7.2lf ms", HeapSortTimes(tempArr, length));
    randIndex = rand() % length; // 0 - (length-1)
    printNum = 5;
    for (int i = 0; i < printNum; i++) {
        if (tempArr[randIndex] >= (length - printNum)) {
            i = 0;
        } else {
            printf("%7d", tempArr[randIndex++]);
        }
    }
    printf("\n");

    for (int i = 0; i < length; i++) {
        tempArr[i] = arr[i];
    }
    printf("  归并排序\t\t%7.2lf ms", MergeSortTimes(tempArr, length));
    randIndex = rand() % length; // 0 - (length-1)
    printNum = 5;
    for (int i = 0; i < printNum; i++) {
        if (tempArr[randIndex] >= (length - printNum)) {
            i = 0;
        } else {
            printf("%7d", tempArr[randIndex++]);
        }
    }
    printf("\n");
}

void knuthShuffle(int arr[], int length) {
    for (int i = length - 1; i > 1; i--) {
        swapInt(&arr[i], &arr[rand() % (i + 1)]);
    }
}

void swapInt(int *card_1, int *card_2) {
    int tCard;
    tCard = *card_1;
    *card_1 = *card_2;
    *card_2 = tCard;
}

double BubbleSortTimes(int arr[], int length) {
    union _LARGE_INTEGER time_start; // 开始时间
    union _LARGE_INTEGER time_over; // 结束时间
    LARGE_INTEGER f; // 计时器频率
    QueryPerformanceFrequency(&f);
    double dqFreq = (double) f.QuadPart; // 计时器频率
    QueryPerformanceCounter(&time_start); // 计时开始

    int temp;
    for (int i = 0; i < length - 1; i++) { // 外层循环：轮次
        int index = -1;
        for (int j = 0; j < length - 1 - i; j++) { // 内层循环：比较并交换位置(找出每轮最大数)
            if (arr[j] > arr[j + 1]) {
                temp = arr[j + 1];
                arr[j + 1] = arr[j];
                arr[j] = temp;
                index++;
            }
        }
        if (index == -1) {
            break; // 为提高排序效率，如果在每轮排序中未发生一次位置交换则代表已经是需要的顺序(直接跳出排序)
        }
    }

    QueryPerformanceCounter(&time_over); // 计时结束
    // 乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
    double run_time = 1000000.0 * (time_over.QuadPart - time_start.QuadPart) / dqFreq;
    return run_time / 1000.0;
}

double SelectSortTimes(int arr[], int length) {
    struct timespec start;
    struct timespec end;
    // 开始时间
    clock_gettime(CLOCK_PROCESS_CPUTIME_ID, &start);

    for (int i = 0; i < length - 1; i++) {
        int minIndex = i; // 最小数的下标
        int min = arr[i]; // 最小数的值
        for (int j = i + 1; j < length; j++) { // 选出本轮最小值，放到当前位置
            if (min > arr[j]) { // 升序排序
                min = arr[j];
                minIndex = j;
            }
        }
        // 将最小值，放在arr[i] (即交换)
        if (minIndex != i) { // 如果当前位置的数就是最小值，那么不需要进行交换
            arr[minIndex] = arr[i];
            arr[i] = min;
        }
    }

    // 结束时间
    clock_gettime(CLOCK_PROCESS_CPUTIME_ID, &end);
    // 总耗时
    // 转化为 ms 为单位（但是精度可以直接到 ns 级别）
    double start_ms = start.tv_sec * 1000.0 + start.tv_nsec / 1000000.0;
    double end_ms = end.tv_sec * 1000.0 + end.tv_nsec / 1000000.0;
    return end_ms - start_ms;
}

double HeapSortTimes(int arr[], int length) {
    union _LARGE_INTEGER time_start; // 开始时间
    union _LARGE_INTEGER time_over; // 结束时间
    LARGE_INTEGER f; // 计时器频率
    QueryPerformanceFrequency(&f);
    double dqFreq = (double) f.QuadPart; // 计时器频率
    QueryPerformanceCounter(&time_start); // 计时开始

    int temp;
    // 将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆
    for (int i = length / 2 - 1; i >= 0; i--) {
        adjustHeap(arr, i, length);
    }
    for (int i = length - 1; i > 0; i--) {
        // 将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端
        temp = arr[i];
        arr[i] = arr[0];
        arr[0] = temp;
        // 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序
        adjustHeap(arr, 0, i); // 从最顶端 下标0 开始重新调整为堆
    }

    QueryPerformanceCounter(&time_over); // 计时结束
    // 乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
    double run_time = 1000000.0 * (time_over.QuadPart - time_start.QuadPart) / dqFreq;
    return run_time / 1000.0;
}

void adjustHeap(int arr[], int i, int length) {
    // 取出当前元素的值，保存为临时变量
    int temp = arr[i];
    // k=i*2+1：k是i结点的左子结点
    for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
        // 在保证有右子结点的前提下，比较左子结点和右子结点的值的大小
        if (k + 1 < length && arr[k] < arr[k + 1]) {
            k++; // 如果右子结点大于左子结点，则把 左子结点 赋值为 右子结点
        }
        // 如果子结点大于父结点
        if (arr[k] > temp) {
            arr[i] = arr[k]; // 把当前子结点的值赋值给父结点
            i = k; // 把当前子结点作为新的父结点，继续向下循环比较是否还有子结点
        } else {
            break; // 直到以 i 父结点的树无子结点未比较为止
        }
    }
    //当for 循环结束后，我们已经将以i 为父结点的树的最大值，放在了 最顶(局部)
    arr[i] = temp; // 将temp值放到调整后的被交换的位置(子结点)
}

double MergeSortTimes(int arr[], int length) {
    union _LARGE_INTEGER time_start; // 开始时间
    union _LARGE_INTEGER time_over; // 结束时间
    LARGE_INTEGER f; // 计时器频率
    QueryPerformanceFrequency(&f);
    double dqFreq = (double) f.QuadPart; // 计时器频率
    QueryPerformanceCounter(&time_start); // 计时开始

    int tempArr[length];
    mergeSort(arr, 0, length - 1, tempArr);

    QueryPerformanceCounter(&time_over); // 计时结束
    // 乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
    double run_time = 1000000.0 * (time_over.QuadPart - time_start.QuadPart) / dqFreq;
    return run_time / 1000.0;
}

void mergeSort(int arr[], int left, int right, int temp[]) {
    if (left < right) {
        int mid = (left + right) / 2;
        // 左边分 递归分法
        mergeSort(arr, left, mid, temp);
        // 右边分 递归分法
        mergeSort(arr, mid + 1, right, temp);
        // 合并法
        merge(arr, left, mid, right, temp);
    }
}

void merge(int arr[], int left, int mid, int right, int temp[]) {
    int i = left; // 初始化 i, 左边有序序列的初始索引
    int j = mid + 1; // 初始化 j, 右边有序序列的初始索引
    int t = 0; // 指向 temp 数组的当前索引
    while (i <= mid && j <= right) { // 只要左边或者右边的索引超过
        if (arr[i] <= arr[j]) { // 左右索引元素开始比较，如果左边小于等
            // 于右边索引元素值，将小的元素赋值到temp数组中
            temp[t++] = arr[i++]; // 索引向后 ++ 移动
        } else {
            temp[t++] = arr[j++];
        }
    }
    // 如果左边有剩余
    while (i <= mid) {
        temp[t++] = arr[i++];
    }
    // 如果右边有剩余
    while (j <= right) {
        temp[t++] = arr[j++];
    }
    t = 0;
    int tempLeft = left;
    while (tempLeft <= right) {
        arr[tempLeft++] = temp[t++];
    }
}

实验结果

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/879523.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

TypeScript的泛型是什么，泛型约束是什么？

TypeScript的泛型是什么，泛型约束是什么？

目录 一、泛型定义 二、泛型函数 1. 定义泛型函数 2. 调用泛型函数 3.简化泛型函数调用 三、泛型约束 1. 指定更加具体的类型 2. 添加约束 3.多个类型变量 四、泛型接口 一、泛型定义 在TypeScript中的泛型&#xff08;Generics&#xff09;允许我们在保证类型安全前…
阅读更多...
微信小程序开发--4.2预览文件/图片

微信小程序开发--4.2预览文件/图片

预览文件 wx.downloadFile({url:, success (res) {console.log(res)if (res.statusCode 200) {wx.openDocument({filePath: res.tempFilePath, showMenu: true,fileType: "xlsx",//文件类型success: function (res) {},fail:function(err){}})}}}) wx.openDocumen…
阅读更多...
IO多线程newfd问题

IO多线程newfd问题

1&#xff0c;多线程中的newfd&#xff0c;能否修改成全局&#xff1f; 答&#xff1a;不能&#xff0c;代码如下。 一共挂了4个客户端&#xff0c;前3个只能运行1次&#xff0c;第4个客户端可以发送多次。 说明后面的客户端覆盖了之前的客户端。前面的客户端一直阻塞在acce…
阅读更多...
【力扣每日一题】2023.8.15 字符中的查找与替换

【力扣每日一题】2023.8.15 字符中的查找与替换

目录 题目&#xff1a; 示例&#xff1a; 分析&#xff1a; 代码&#xff1a; 题目&#xff1a; 示例&#xff1a; 分析&#xff1a; 题目很长&#xff0c;简而言之就是检查字符串中对应索引的位置是否有特定的字符串&#xff0c;如果有&#xff0c;那么替换&#xff0c;返…
阅读更多...
点击base64编码过的图片在另一个页面显示

点击base64编码过的图片在另一个页面显示

开始的代码是这样的&#xff0c;新开一个窗口显示经过base64编码后的图片&#xff0c;但是url太长了显示失败。 openImage(imgSrc) {window.open(imgSrc, _blank); }, 解决方法&#xff1a;这段代码接收一个Base64编码的图像数据&#xff0c;把它转换为一个Blob对象。 Blob&…
阅读更多...
《算法竞赛·快冲300题》每日一题：“房间划分”

《算法竞赛·快冲300题》每日一题：“房间划分”

《算法竞赛快冲300题》将于2024年出版&#xff0c;是《算法竞赛》的辅助练习册。 所有题目放在自建的OJ New Online Judge。 用C/C、Java、Python三种语言给出代码&#xff0c;以中低档题为主&#xff0c;适合入门、进阶。 文章目录 题目描述题解C代码Java代码Python代码 “ 房…
阅读更多...
考公-判断推理-组合排列

考公-判断推理-组合排列

例题 例题 例题 代入法 例题 排除法 例题
阅读更多...
AMD限制资源用量CU_MASK

AMD限制资源用量CU_MASK

通过配置两个环境变量来控制进程所使用的CU&#xff1a; CU_MASK_0 CU_MASK_1 举例&#xff1a; 使用每个ES中的一半CU则配置如下&#xff1a; export CU_MASK_00xcccccccc export CU_MASK_10xcccccccc
阅读更多...
判断推理 -- 图形推理 -- 位置规律

判断推理 -- 图形推理 -- 位置规律

一组图&#xff1a;从前往后找规律。 二组图&#xff1a;从第一组图找规律&#xff0c;第二组图应用规律。 九宫格&#xff1a; 90%横着看找规律&#xff0c;第一行找规律&#xff0c;第二行验证规律&#xff0c;第三行应用规律。 所有有元素组成都是线&#xff0c;三角形&…
阅读更多...
【C++ STL基础入门】初识STL

【C++ STL基础入门】初识STL

文章目录 前言一、STL是什么&#xff1f;1.STL概念2.容器是什么&#xff1f;3.STL的优势 二、将会学习到的stl和算法1.将会学到的容器2.算法3.字符串基础字符串字符串视图(basic_string_view) 总结 前言 本系列STL是以VS2022为编译器&#xff0c;C20为标准来写的一套STL。 ST…
阅读更多...
笔记04：全局内存

笔记04：全局内存

一、CUDA内存模型概述 寄存器、共享内存、本地内存、常量内存、纹理内存和全局内存 一个核函数中的线程都有自己私有的本地内存。 一个线程块有自己的共享内存&#xff0c;对同一个线程块中所有的线程都可见&#xff0c;其内容持续线程块的整个生命周期。 所有线程都可以访问…
阅读更多...
武汉地铁19号线完成5G专网全覆盖，现场测试下行速率超千兆！

武汉地铁19号线完成5G专网全覆盖，现场测试下行速率超千兆！

近日&#xff0c;极目新闻记者从中国移动湖北公司获悉&#xff0c;随着武汉地铁19号线全线隧道正式贯通&#xff0c;湖北移动目前已完成新月溪公园至鼓架山站5G网络覆盖&#xff0c;轨行区5G专网全覆盖&#xff0c;并成功进行试车验证&#xff0c;19号线成为国内首条全线实现5G…
阅读更多...
互联网发展历程：从中继器口不够到集线器的引入

互联网发展历程：从中继器口不够到集线器的引入

互联网的发展&#xff0c;就像一场不断演进的技术盛宴&#xff0c;每一步的变革都在推动着我们的世界向前。然而&#xff0c;在网络的早期&#xff0c;一项重要的技术问题曾困扰着人们&#xff1a;当中继器的接口数量不足时&#xff0c;如何连接更多的设备&#xff1f;这时&…
阅读更多...
C#_Array类型

C#_Array类型

简介 公共语言运行时中所有数组的基类、抽象类&#xff0c;用于创建、处理、搜索、排序数组。 常用属性 Rank&#xff1a;获取数组维数&#xff08;在多维数组中采用有序整数来标注&#xff0c;例如一维数组、二维数组、三维数组&#xff09;&#xff0c;数量从1开始。 leng…
阅读更多...
记录--form 表单恢复初始数据

记录--form 表单恢复初始数据

这里给大家分享我在网上总结出来的一些知识&#xff0c;希望对大家有所帮助 form 表单恢复初始数据 在现代的 Web 开发中&#xff0c;表单是不可或缺的组件之一。用户可以通过表单输入和提交数据&#xff0c;而开发者则需要对这些数据进行处理和存储。然而&#xff0c;在某些情…
阅读更多...
web基础入门和PHP语言基础入门 一

web基础入门和PHP语言基础入门 一

web基础入门和php语言基础入门 一 WEB简介与HTTP入门WEB简介HTTP 简介HTTP 请求报文&#xff1a;请求方法&#xff1a;请求头部&#xff1a;&#xff08;常见的请求头&#xff09;HTTP 响应报文&#xff1a;响应状态码&#xff1a;Cookie HTML入门学习什么是HTML什么是标记语言…
阅读更多...
调试 SELinux

调试 SELinux

semanage port -a -t http_port_t -p tcp 82 题目&#xff1a; 非标准端口 82 上运行的 WEB 服务器在提供内容时遇到问题。根据需要调试并解决问题&#xff0c; 并使其满足以下条件&#xff1a; 系统上的 web 服务器能够提供/var/www/html 中所有现在有的 html 文件&#xff…
阅读更多...
分享一个使用Java工具类——git格式图片裁剪重组

分享一个使用Java工具类——git格式图片裁剪重组

git格式图片裁剪重组 有时候需要自己录制一个gif图片的时候就不知道去哪里录制&#xff0c;所以只能在百度找一个可以录制gif图片的软件&#xff0c;但是你会发现&#xff0c;你能找到的免费导出的都是有水印的&#xff0c;所以你可能就需要找一个水印少一点的软件了&#xff…
阅读更多...
AI黑马挑战赛，探索研发新趋势丨IDCF

AI黑马挑战赛，探索研发新趋势丨IDCF

随着AI的出现&#xff0c;获取知识的成本大幅降低&#xff0c;当DevOps与AI相结合时&#xff0c;必将产生全新的化学反应。不断涌现的AI新工具提醒我们&#xff0c;一个全新的研发工作范式正在逐渐形成。而DevOps的核心理念是敏捷协同&#xff0c;作为工程师&#xff0c;如何通…
阅读更多...
印度通过《2023年数字个人数据保护法案》

印度通过《2023年数字个人数据保护法案》

2023年8月7日&#xff0c;印度议会下议院&#xff08;Lok Sabha&#xff09;通过《2023年数字个人数据保护法案》&#xff08;Digital Personal Data Protection Bill 2023&#xff09;。8月9日&#xff0c;该法案获得上议院&#xff08;Rajya Sabha&#xff09;批准。 - 该法案…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023