目录
前言
冒泡排序
选择排序
插入排序
希尔排序
归并排序
快速排序
堆排序
计数排序
桶排序
基数排序
十大排序之间的比较
总结
前言
学了数据结构之后一直没有进行文字性的总结，现在趁着还有点时间把相关排序的思路和代码实现来写一下。概念的话网上都有，主要就是总结一下代码以及排序之间的比较。
冒泡排序
冒泡排序_百度百科 (baidu.com)
https://baike.baidu.com/item/%E5%86%92%E6%B3%A1%E6%8E%92%E5%BA%8F/4602306
冒泡排序算法_lu_1079776757的博客-CSDN博客https://blog.csdn.net/lu_1079776757/article/details/80459370?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193930816800192229801%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=169193930816800192229801&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~hot_rank-12-80459370-null-null.142%5Ev92%5Einsert_down1&utm_term=%E5%86%92%E6%B3%A1%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187 冒泡排序是比较基础的排序了，最开始还没学数据结构之前学的两个排序就是冒泡排序以及选择排序，两个的实现原理都相对比较简单，冒号排序就想象一个像气泡一样把最大值或者最小值浮上来或者沉下去。假设是需要进行从小到大进行排序，就可以先把第一位拿出来与后面的进行挨个比较，如果说后面待比较的数较小就进行交换，更新这个较大的值，这样逐个比较之后那可以确定是整个数组的最大值是在最后面了。因为我们是逐个比较的，假设前面有比最后还大的数，那显然会被交换到最后，所以假设不成立。按照同样的方法可以把第二大的数移动到倒数第二的位置，把第三大的数移动到倒数第三的位置……以此类推实现整个数组的排序。
代码思路：根据前面的分析，可能有点乱，在这里再梳理一下，还是以从小到大排序，每一趟的比较都可以确定将相对大的数移动到数组的末尾，这个时候就需要思考一下几个问题。一共需要多少趟？每趟比较的次数是固定吗？
每次可以把大的数冒泡到最后，假设有十个元素，我们把最大值移动到arr[9]的位置，那么下次的范围就是[0-9),在新的范围内找最大值，以此类推，你们最后一次只有一个元素还需要比较吗？可以认为是不需要比较的，也就是需要9趟（数组元素个数-1），同样的比较的次数也随着范围的缩小而减少，相信大家已经找到了规律，可以自己尝试一下了。
为什么是把最大值移动到最后，反而是较小才交换呢，因为他的指针是一直往后面移动的，指向的始终是最大值的位置，所以保证的是指针移动后的数是“最大值”的位置，所以后面的值较小的时候进行交换。
#include<stdio.h>
int main(){
int arr[10]={1,3,5,7,9,0,8,6,4,2};
int i,j;
int tmp=arr[0];
printf("原始数组为：");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
for(i=1;i<10;i++){//控制轮数
for(j=0;j<10-i;j++){//控制交换的次数
if(arr[j]>arr[j+1]){//如果后面的数较小就进行交换
tmp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=tmp;
}
}
}
printf("排序后的数组为：");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
return 0;
}尽量代码写的简短一点，所以把数组设计成固定长度，而且内容不是用户输入的这样了，大家可以自己尝试其他的形式，当然这个是把值移动到数组的末尾的形式，可能会有人认为这个不算冒泡排序，他是把泡沉下去的，那他这样想的话你也可以把泡“冒出来”，还是从小到大排序，那你的思路就是把最小值移动到数组的开头，依此类推……
#include<stdio.h>
int main(){
int arr[10]={1,3,5,7,9,0,8,6,4,2};
int i,j;
int tmp=arr[0];
printf("原始数组为：");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
for(i=0;i<9;i++){//控制轮数
for(j=9;j>i;j--){//控制交换的次数
if(arr[j-1]>arr[j]){//如果前面的数较大就进行交换
tmp=arr[j];
arr[j]=arr[j-1];
arr[j-1]=tmp;
}
}
}
printf("排序后的数组为：");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
return 0;
}
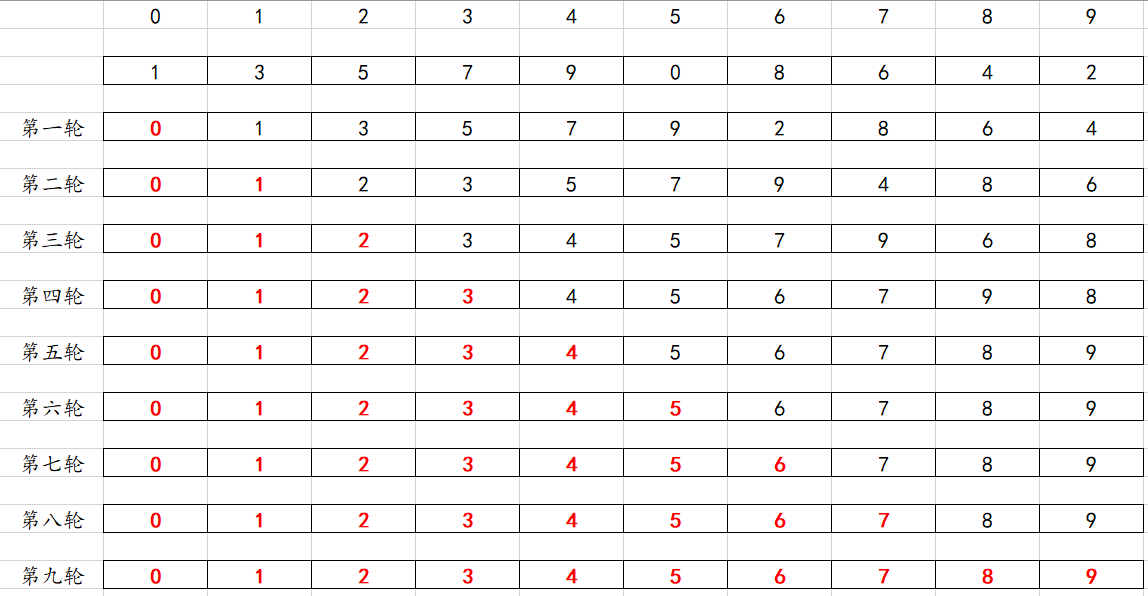
到这里就完了吗？当然不是，冒泡排序遇到特殊的情况可以进行改良，当一个数组比较有序的时候，冒泡排序还是会一直比较，但实际上他很多的比较都是无效的。
#include<stdio.h>
int main(){
int arr[10]={1,3,5,7,9,0,8,6,4,2};
int i,j;
int tmp=arr[0];
int sheavesNumber=0;//累计轮数
int comparisonsNumber=0;//比较次数
int exchangesNumber=0;//交换次数
printf("原始数组为：");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
for(i=0;i<9;i++){//控制轮数
sheavesNumber++;
for(j=9;j>i;j--){//控制交换的次数
comparisonsNumber++;
if(arr[j-1]>arr[j]){//如果前面的数较大就进行交换
tmp=arr[j];
arr[j]=arr[j-1];
arr[j-1]=tmp;
exchangesNumber++;
}
}
}
printf("排序后的数组为：");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
printf("此次排序一共经过了%d趟\n一共经历了%d次比较\n一共进行了%d交换\n",
sheavesNumber,comparisonsNumber,exchangesNumber);
return 0;
} 
#include<stdio.h>
int main(){
int arr[10]={1,3,5,7,9,0,8,6,4,2};
int i,j;
int tmp=arr[0];
int sheavesNumber=0;//累计轮数
int comparisonsNumber=0;//比较次数
int exchangesNumber=0;//交换次数
bool flag=true;//标记还是否需要排序
printf("原始数组为：");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
for(i=0;i<9;i++){//控制轮数
flag=false;
sheavesNumber++;
for(j=9;j>i;j--){//控制交换的次数
comparisonsNumber++;
if(arr[j-1]>arr[j]){//如果前面的数较大就进行交换
tmp=arr[j];
arr[j]=arr[j-1];
arr[j-1]=tmp;
exchangesNumber++;
flag=true;//还需要
}
}
if(!flag)break;
}
printf("排序后的数组为：");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
printf("此次排序一共经过了%d趟\n一共经历了%d次比较\n一共进行了%d交换\n",
sheavesNumber,comparisonsNumber,exchangesNumber);
return 0;
}
这个数组只需要6趟的比较就已经可以实现排序， 交换的次数没有改变，但是比较的次数减少了。那么这个是怎么实现的呢？
用一个变量标记是否需要进行下一趟比较，每一趟都标记不需要进行下一趟的比较，如果出现了要交换的时候，就比较还需要进行下一趟比较。因为他的比较是相邻的进行比较，以从小到大排序为例，如果没有出现交换则说明他相邻左边的数会比他小，相邻右边的数会比他大，对于所以元素都是，这不就是排序好的数组吗。
假设数组元素为这个，大家可以自己试着比较一下，看会进行多少次的比较。
int arr[10]={0,1,2,3,4,5,6,7,8,9};选择排序
选择排序_百度百科 (baidu.com)https://baike.baidu.com/item/%E9%80%89%E6%8B%A9%E6%8E%92%E5%BA%8F/9762418
选择排序（c语言）_我滴天呐我去的博客-CSDN博客https://blog.csdn.net/m0_59083833/article/details/123971321?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193937416800226598783%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=169193937416800226598783&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~hot_rank-5-123971321-null-null.142%5Ev92%5Einsert_down1&utm_term=%E9%80%89%E6%8B%A9%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187 选择排序就是每次选出最大或者最小的元素出来，与数组前面的位置进行交换，这个其实当时有一个疑问，这个交换我不确实是不是需要每次都进行交换，感觉这两种都算选择排序，有知道的大佬可以指正一下。还是以从小到大排序为例。
思路一：经过遍历每次选出最小值的时候进行交换。
for(i=0;i<9;i++){
for(j=i+1;j<10;j++){
if(arr[i]>arr[j]){//如果后面有比他的小的就更新
tmp=arr[i];
arr[i]=arr[j];
arr[j]=tmp;
}
}
}
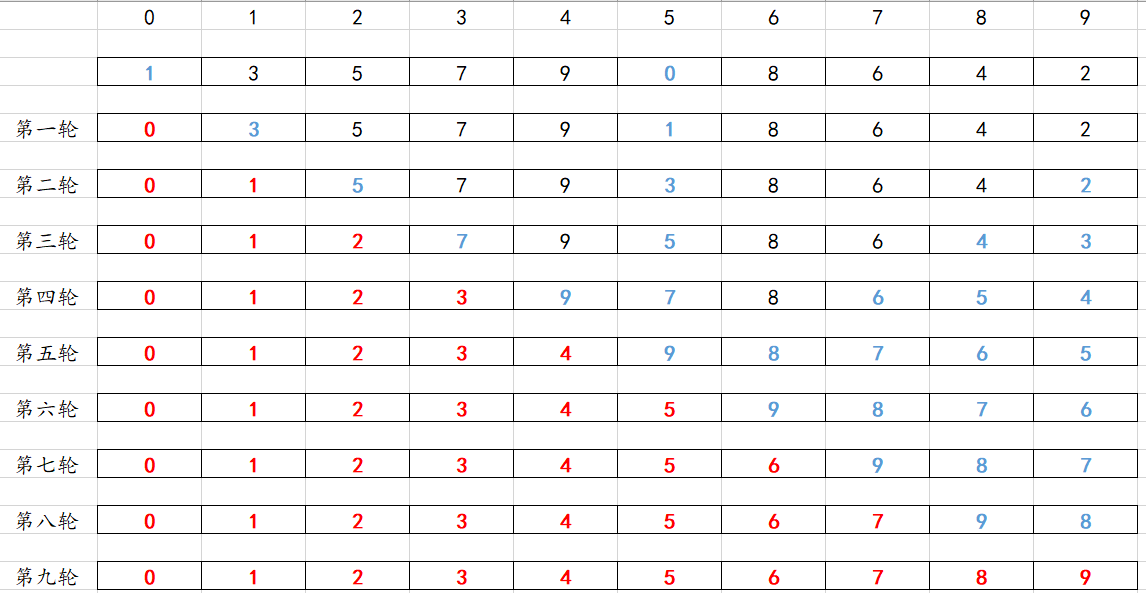
思路二：遍历选出最小值的时候先不进行交换，只是保留下标，到最后才进行交换。
for(i=0;i<9;i++){
tmp=arr[i];
x=i;
for(j=i+1;j<10;j++){
if(tmp>arr[j]){//如果后面有比他的小的就更新
tmp=arr[j];
x=j;
}
}
arr[x]=arr[i];
arr[i]=tmp;
}
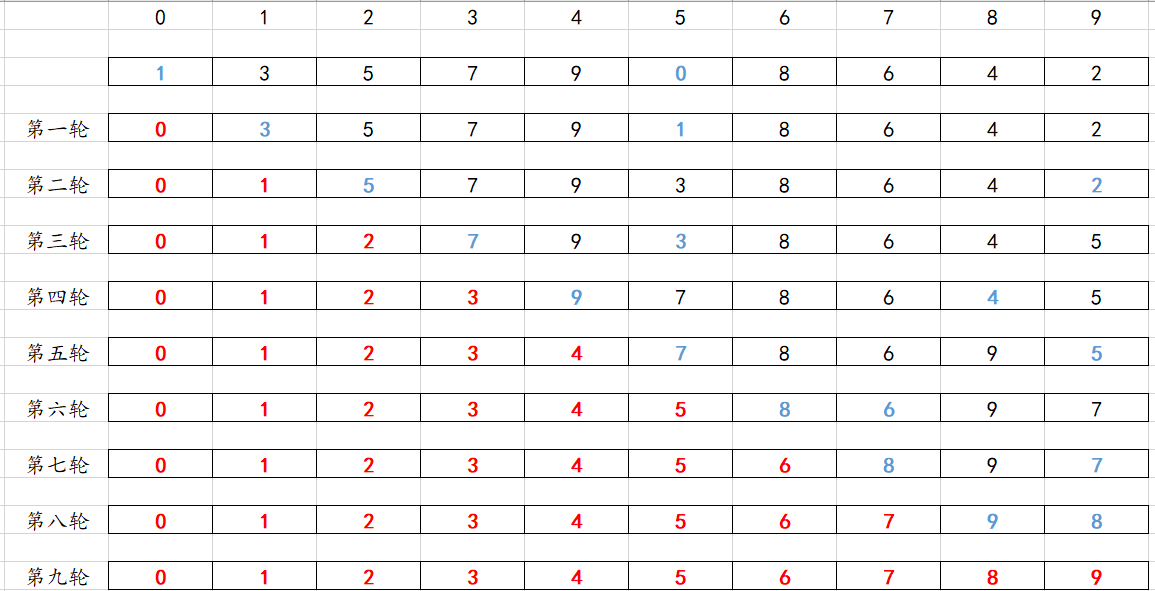
不知道大家能不能get到那个点，更新肯定是需要更新他的值的，他的交换需要是数组内部交换，但是交换的次数第一种是每次都交换的，第二种是保存下标之后在最后进行一次的交换。默认下面都是从小到大排序。
插入排序
插入排序_百度百科 (baidu.com)https://baike.baidu.com/item/%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F?fromModule=lemma_search-box
插入排序（图解）_RainySouL1994的博客-CSDN博客https://blog.csdn.net/qq_33289077/article/details/90370899?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193945216800180639289%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=169193945216800180639289&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~hot_rank-5-90370899-null-null.142%5Ev92%5Einsert_down1&utm_term=%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187 插入排序就是把元素插入到一个有序的数组里面，可以默认一个元素自身是有序的，然后再拿出一个元素和那个元素比较，看是插入到他的前面还是后面，这样确保两个元素是有序的，再拿出一个元素按照同样的方法插入到前面两个已经有序的位置中，以此类推最终全部有序。
代码思路：他是拿元素插入到有序的数组中，从后面往前面比较，如果说他比最后一个大，那他肯定是比前面所有元素都大（因为他是插入到有序的数组中），所以就可以直接结束了，如果他比最后一个元素小，就进行往前面比较，直到移动到数组开头，那他就成为新的开头了。
for(i=1;i<10;i++){//默认arr[0]自身是有序的
tmp=arr[i];
//值小才继续往前面找
for(j=i-1;tmp<arr[j]&&j>=0;j--){
tmp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=tmp;
}
}注意我这里是偷了一个懒，tmp的值始终是有意义的tmp的值为arr[j+1],如果交换的时候先是tmp=arr[j]，结果是不正确的，这个记忆的方法就是tmp的赋值是arr[i]的值，在内层循环里面，j初值为i-1，tmp=arr[j+1]就还是tmp=arr[i]。j的值是逐渐减小的，对于从小到大排序的数组也是逐渐减小的，tmp在内层循环表示的值始终不能发生改变。可以把数组元素换少一点自己跟着代码过一遍。
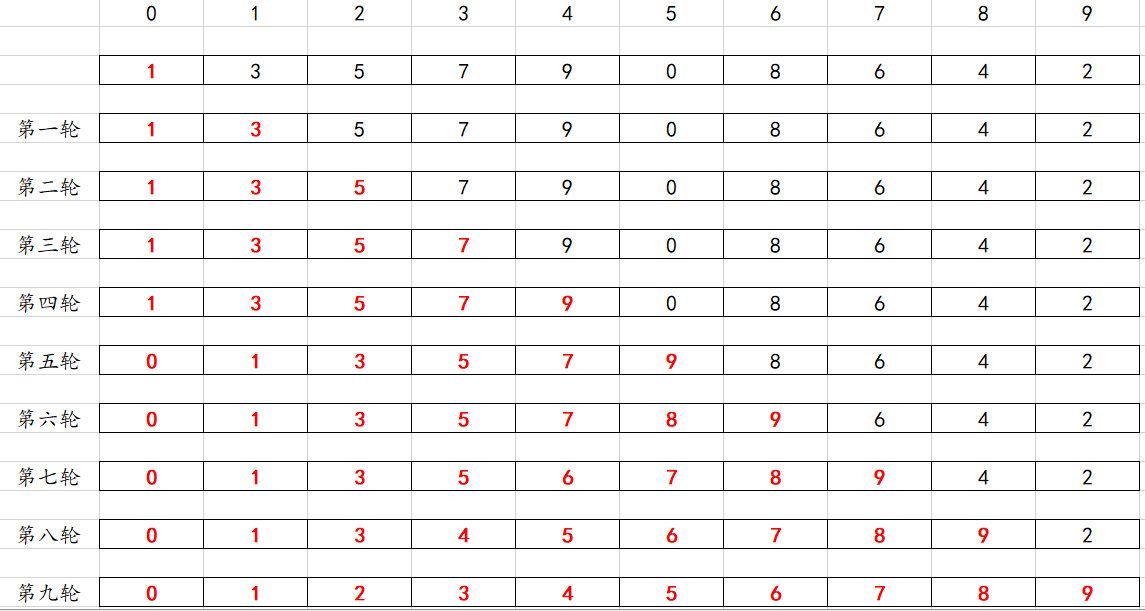
希尔排序
希尔排序_百度百科 (baidu.com)https://baike.baidu.com/item/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F?fromModule=lemma_search-box
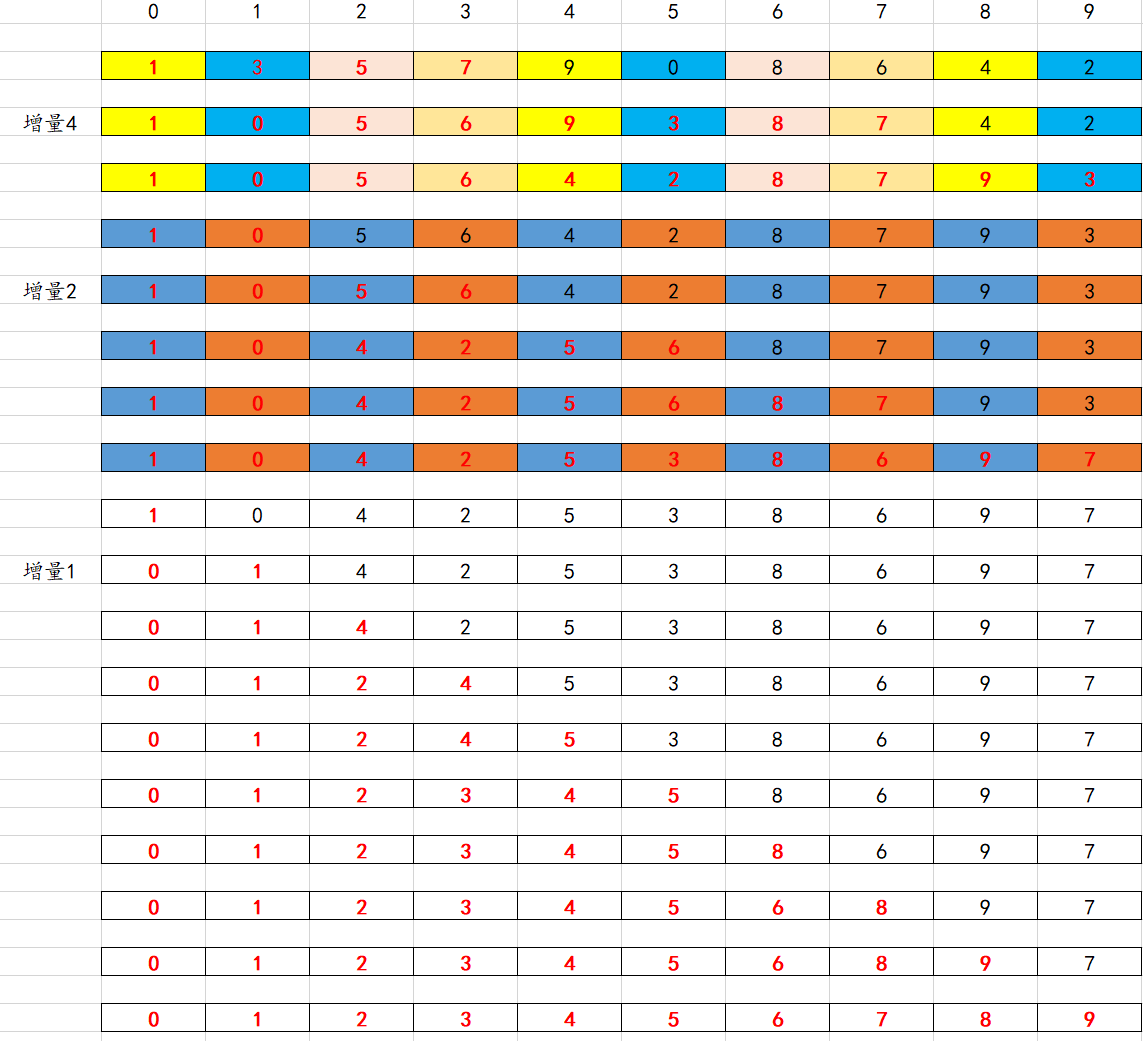
理解希尔排序的排序过程_razor521的博客-CSDN博客https://blog.csdn.net/weixin_37818081/article/details/79202115?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193949316800180692570%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=169193949316800180692570&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~hot_rank-3-79202115-null-null.142%5Ev92%5Einsert_down1&utm_term=%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187 希尔排序的思路和插入排序差不多，当他的增量为1的时候就是之前提到的插入排序了。当他为10个元素的时候可能就不是一个一个来实现插入排序，他可能是分组来进行插入，0,4,8位置拿出来变成一组进行插入排序，1,5,9位置上的元素拿出来进行插入排序，2,6上面的元素拿出来进行排序，3,7上面的元素为一组拿出来进行排序，然后再缩短他的增量，0,2,4,6,8为一组，1,3,5,7,9为另一组，最后还是要进行增量为1的排序，整个过程就逐渐变得有序了。
理解就是插入排序是和相邻的元素进行排序，希尔排序是跨着增量比较。
#include<stdio.h>
int main(){
int arr[10]={1,3,5,7,9,0,8,6,4,2};
int i=0,j=0;
int tmp=arr[0];
int step=4;//假设增量为4
int count=1;//第几次排序
printf("原始数组为：\n");
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
while(step!=0){
for(i=step;i<10;i++){//默认arr[0]自身是有序的
tmp=arr[i];
//值小才继续往前面找
for(j=i-step;tmp<arr[j]&&j>=0;j-=step){
tmp=arr[j+step];
arr[j+step]=arr[j];
arr[j]=tmp;
}
}
printf("第%d次排序后的数组为：此时的增量为%d\n",count,step);
for(i=0;i<10;i++){
if(i!=9){
printf("%-3d",arr[i]);
}else{//最后一个进行换行输出
printf("%-3d\n",arr[i]);
}
}
step/=2;//每次增量减半
count++;//排序次数增加
}
return 0;
}
归并排序
归并排序_百度百科 (baidu.com)https://baike.baidu.com/item/%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F?fromModule=lemma_search-box
十大经典排序算法-归并排序算法详解_小小学编程的博客-CSDN博客https://blog.csdn.net/qq_35344198/article/details/106857042?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193952316800182129410%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=169193952316800182129410&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~hot_rank-1-106857042-null-null.142%5Ev92%5Einsert_down1&utm_term=%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187 这个用分治的思路还是比较好理解，先把一个数组对半分割，直到含义一个元素为止，然后进行合并，按照他的排序规则（以从小到大为例），就是每次从队头拿出一个元素来进行比较，谁小就拿出来放前面，如果被拿出元素的指针往后面移动，进行第二次的比较。
代码思路：arr是原始数组，tmp是临时数组，left是指向arr的起点，right指向arr最后一个元素的位置，mid指向中间的位置。所以按照mid可以将数组分成两半[left,mid],[mid,right],都可以取到，这里默认的是arr不一定有序，但是分成两断的数组是有序的，就是将两边的元素合成一个整体有序的数组，假设[leift,right]表示数组a，[left,mid]表示数组b,[mid,right]表示数组c，这里b,c是有序的，a不一定是有序的。i，j可以理解成两个指向，指向两个数组的起点，通过判断两个指针指向位置元素的大小来选择拷贝哪个元素，同时进行指针的移动来进行下一个元素的比较，直到两个数组指向的位置有一个越界就结束判断，但是此时总会有一个数组里面的元素没有完全拷贝，假设b里面元素为[1,3]，c里面的元素为[2,4]，此时当a为[1,2,3]的时候就可以结束判断了，但此时c数组里面还有一个元素没有被拷贝，所以还需要将剩下的元素直接进行拷贝（因为单个数组默认是有序的，所以直接拷贝就行）。所以最后的两个直接拷贝元素的循环，两者有且只会中一个，当然因为我们是保存在临时数组里面的，最后还需要将元素拷贝到临时数组里面。
void merge(int arr[],int tmp[],int left,int mid,int right){
int i=left;
int j=mid+1;
int k=left;
while(i!=mid+1 && j!=right+1){
if(arr[i]<=arr[j]){
tmp[k++]=arr[i++];
}else{
tmp[k++]=arr[j++];
}
}
while(i!=mid+1){//将剩下的元素进行拷贝
tmp[k++]=arr[i++];
}
while(j!=right+1){//将剩下的元素进行拷贝
tmp[k++]=arr[j++];
}
for(i=0;i<=right;i++){//将临时保存的元素拷贝到元素数组中
arr[i]=tmp[i];
}
}接下来就是如何确保他分成的两边是有序的，这里就是用到分治的思想，最后直接分成1个元素的数组（left>=right），此时默认就是有序的了，然后在一层一层往外面扩，就总体有序了。
void mergeSort(int arr[],int tmp[],int left,int right){
if(left<right){
int mid=left+(right-left)/2;
mergeSort(arr,tmp,left,mid);
mergeSort(arr,tmp,mid+1,right);
merge(arr,tmp,left,mid,right);
}
}tmp是临时存储元素的空间，这里实参是（0,9）。
int arr[10]={1,3,5,7,9,0,8,6,4,2};
int tmp[10];
mergeSort(arr,tmp,0,9);
快速排序
快速排序算法_百度百科 (baidu.com)https://baike.baidu.com/item/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95?fromtitle=%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F&fromid=2084344&fromModule=lemma_search-box
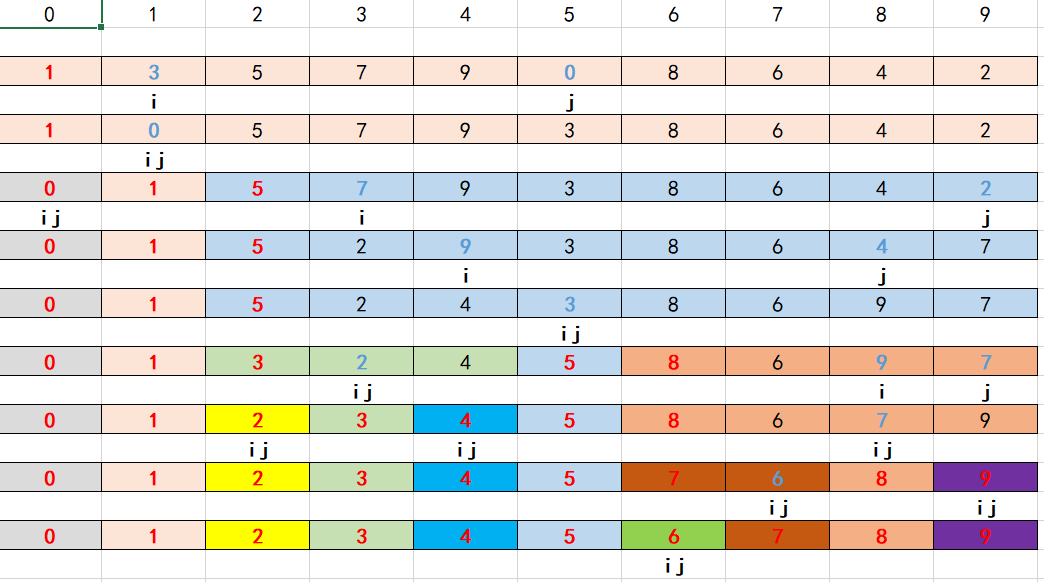
快速排序详解_凉夏y的博客-CSDN博客https://blog.csdn.net/LiangXiay/article/details/121421920?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193959616800222853141%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=169193959616800222853141&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~hot_rank-2-121421920-null-null.142%5Ev92%5Einsert_down1&utm_term=%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187代码思路：先把数组0号位置上面的元素当成一个基准，i先是指向起始点，j是指向终点，然后进入外层循环，经过两个内层循环之后，i指向的是大于arr[0]元素的位置，j指向的是小于arr[0]元素的位置，再进行交换，意思就是说把大于arr[0]的都放在他的右边，把小于arr[0]的元素都放在他的左边，那么arr[0]元素的位置在整个数组里面就确定了，然后根据arr[0]的值进行数组分割，把大于的部分当成一个新数组，把小于的部分当成另一个数组，重复整个过程。right指向最后一个元素的下标，left指向起始位置的下标。首先当i和j相遇了就说明他比较结束了，里面内层循环的判断肯定是需要是取到等号的，而且是需要对面先移动，如果是以arr[0]为基准，那么先进行移动的就是从终点开始移动的j，一个极端的例子，假设arr[0]上面的值是min，那么如果i先移动，i和j最后就会在1的位置相遇，如果j先移动，结果就会在0号位置上面相遇。快速排序的数组越乱对于结果越好，所以有些时候会先将数组打乱顺序再进行快速排序。
void quickSort(int arr[],int left,int right){
if(left>right)return;
int i=left;
int j=right;
int key=arr[left];
while(i!=j){
while(arr[j]>=key && j>i){
j--;
}
while(arr[i]<=key && j>i){
i++;
}
if(j>i){
int tmp=arr[i];
arr[i]=arr[j];
arr[j]=tmp;
}
}
arr[left]=arr[i];
arr[i]=key;
quickSort(arr,left,i-1);
quickSort(arr,i+1,right);
}
堆排序
堆排序_百度百科 (baidu.com)https://baike.baidu.com/item/%E5%A0%86%E6%8E%92%E5%BA%8F?fromModule=lemma_search-box
堆排序详细图解（通俗易懂）_右大臣的博客-CSDN博客https://blog.csdn.net/weixin_51609435/article/details/122982075?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193925316800215017525%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169193925316800215017525&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-122982075-null-null.142%5Ev92%5Einsert_down1&utm_term=%E5%A0%86%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187&ydreferer=aHR0cHM6Ly9zby5jc2RuLm5ldC9zby9zZWFyY2g%2Fc3BtPTEwMDAuMjExNS4zMDAxLjQ0OTgmcT0lRTUlQTAlODYlRTYlOEUlOTIlRTUlQkElOEYmdD0mdT0%3D这个有一点二叉树的知识就更容易理解一点，这里的堆不是堆栈的那个意思，他是一种近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
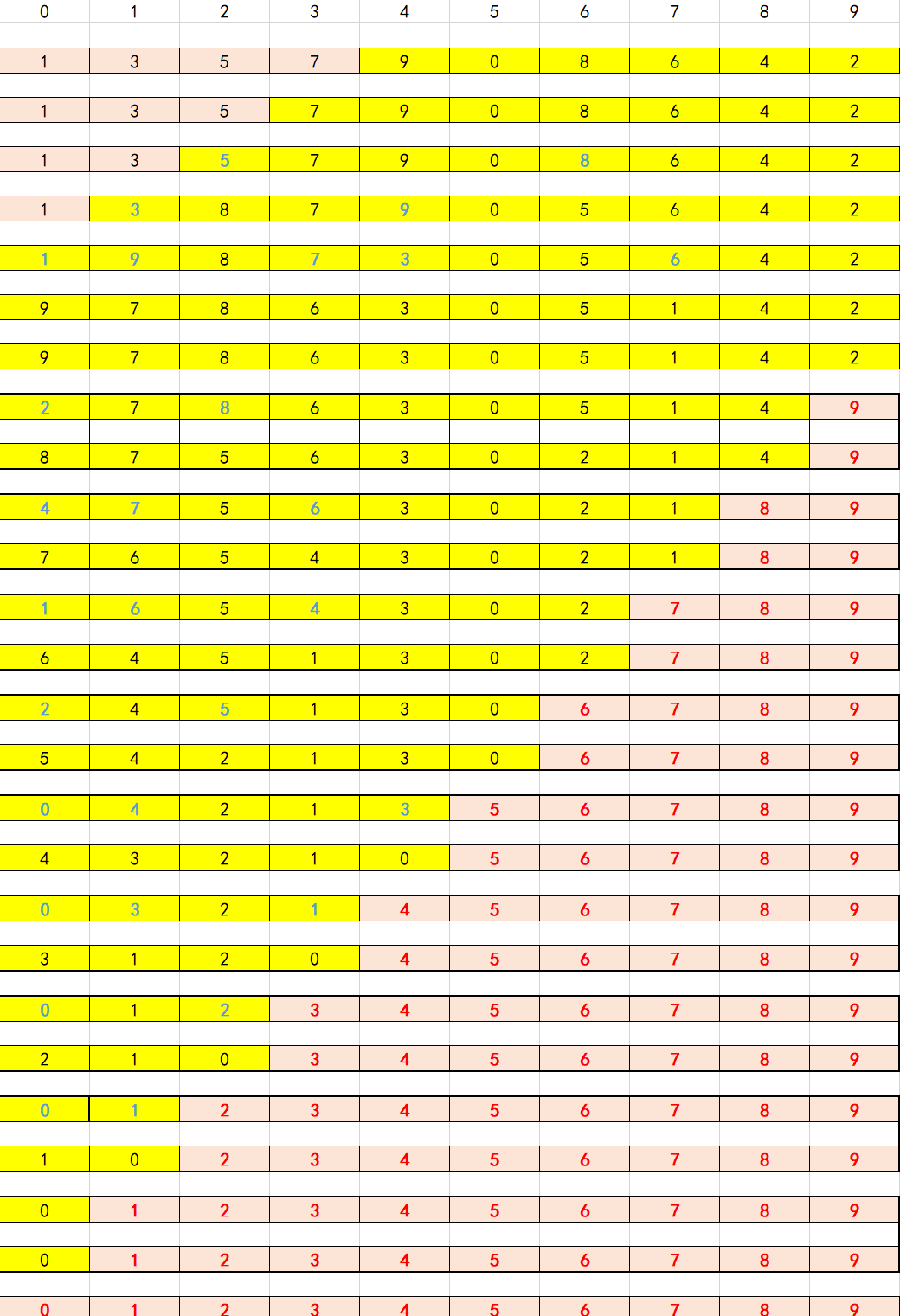
代码思路，这个主要就是要调整成大根堆或者小根堆的形式，他只需要满足父节点大于/小于子节点，左右两个孩子之间的大小比较不需要管，这样的好处就是对于位置的调整就不在是线性的了。
最开始构造的话是从最后一颗子树开始从后往前进行调整，每次调整从上往下调整。
从小到大排序是构造大根堆，从大到小排序是构造小根堆。
#include<stdio.h>
void heapAdjust(int arr[], int start, int end){
//建立父节点指针和子节点指针
int dad=start;
int son=dad*2+1;
while(son<=end){//若子节点指针在范围内才做比较
if(son+1<=end && arr[son]<arr[son+1])//先比较两个子节点大小，选择最大的
son++;
if(arr[dad]>arr[son])//如果父节点大于子节点代表调整完毕，直接跳出函数
return;
else{ //否则交换父子内容再继续子节点和孙节点比较
int tmp=arr[dad];
arr[dad]=arr[son];
arr[son]=tmp;
dad=son;
son=dad*2+1;
}
}
}
void heapSort(int arr[], int len){
int i=0;
//初始化，i从最后一个父节点开始调整
for(i=len/2-1;i>=0;i--)
heapAdjust(arr,i,len-1);
//先将第一个元素和已经排好的元素前一位做交换，再从新调整，直到排序完毕
for(i=len-1;i>0;i--){
int tmp=arr[0];
arr[0]=arr[i];
arr[i]=tmp;
heapAdjust(arr,0,i-1);
}
}
计数排序
计数排序_百度百科 (baidu.com)https://baike.baidu.com/item/%E8%AE%A1%E6%95%B0%E6%8E%92%E5%BA%8F?fromModule=lemma_search-box
排序——计数排序（Count sort）_努力的老周的博客-CSDN博客https://blog.csdn.net/justidle/article/details/104203972?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193970116800192246345%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=169193970116800192246345&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~hot_rank-2-104203972-null-null.142%5Ev92%5Einsert_down1&utm_term=%E8%AE%A1%E6%95%B0%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187
这个我之前没听过，结果过了一遍发现之前刷题的时候用过几次了，如果这种就是计数排序的话那就简单了，他就是进行统计个数然后输出，用空间换时间。
代码思路：我这里默认的话最小值是大于等于0的数，然后最大值是自己求出来的，其实转换一下的话最小值也可以为负数，那么他的思路是什么呢？
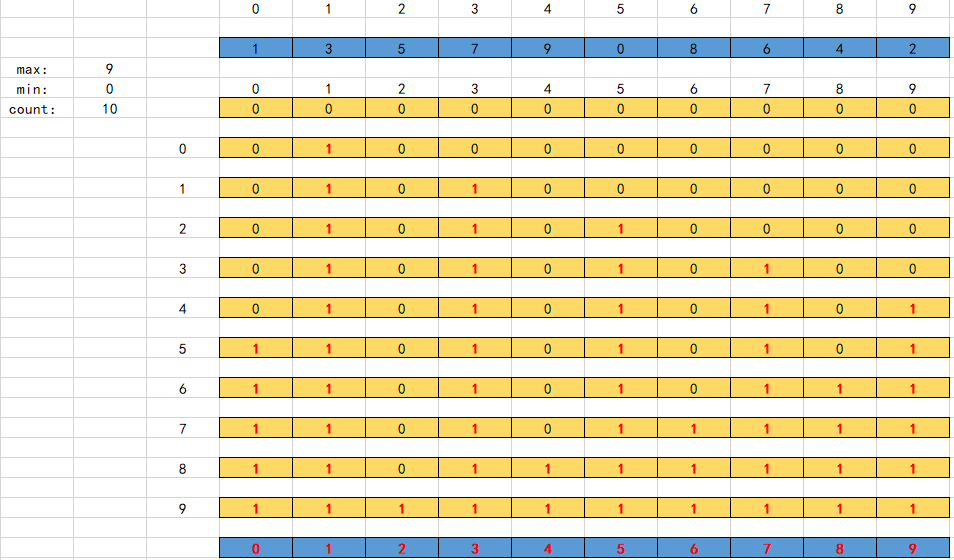
一个数组里面有很多的数，然后会存在最大值max和最小值mix，根据[min,max]可以得到他这个范围内的个数，count=max-min+1,然后就是开辟了这么大的空间，那么这么大的空间可以干嘛呢？当然是直接填数了，因为我们是知道max和min的，那数组其他元素的值肯定也是在这个范围里面，所以就先对count大小的数组元素都初始化为0，有一个就加一，最后统计结束了之后，直接按min到max的范围的输出count数组的下标，count元素的大小就是需要输出几次，这样就可以得到从小到大排序的数组了。
void countSort(int arr[],int n){
int max=arr[0];
int i;
int index=0;
//得到最大值
for(i=0;i<n;i++){
max=max>arr[i]?max:arr[i];
}
//开辟一个[0,max]的辅助空间
int *help=(int *)malloc(sizeof(int)*(max+1));
//数组初始化
for(i=0;i<=max;i++){
help[i]=0;
}
//按照arr数组进行统计个数，保存到help数组中
for(i=0;i<n;i++){
help[arr[i]]++;
}
for(i=0;i<=max;i++){
while(help[i]){
arr[index++]=i;
help[i]--;
}
}
//回收空间
free(help);
}当然我这个比较特殊，没有重复的元素，元素也是连续的，大家可以直接尝试其他的数组，其实这个缺点就很明显了，如果数据比较零散，而且最大值和最小值的差距比较大就不太友好了。
桶排序
桶排序_百度百科 (baidu.com)https://baike.baidu.com/item/%E6%A1%B6%E6%8E%92%E5%BA%8F?fromModule=lemma_search-box
桶排序 （详细图解）_s逐梦少年的博客-CSDN博客https://blog.csdn.net/qq_52253798/article/details/122970542?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193973216800225549120%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169193973216800225549120&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-122970542-null-null.142%5Ev92%5Einsert_down1&utm_term=%E6%A1%B6%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187
这个的话就是先把数组按照他的排序规则先进行大致的分类，再对分类之后的数组用其他排序算法进行排序或者递归用桶排序。这个分类的规则的话还是要根据自己的数据来判断，所以不太好写一个适用的代码，如果是这篇博客用到的那组数据可以用两个桶，一边装小于5的数，一边装大于等于5的数，然后对于两边的数据进行其他算法的排序。
基数排序
基数排序_百度百科 (baidu.com)https://baike.baidu.com/item/%E5%9F%BA%E6%95%B0%E6%8E%92%E5%BA%8F?fromModule=lemma_search-box
排序算法之基数排序_基数排序算法_小C哈哈哈的博客-CSDN博客https://blog.csdn.net/xiaoxi_hahaha/article/details/113186384?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193975816800182720093%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169193975816800182720093&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-113186384-null-null.142%5Ev92%5Einsert_down1&utm_term=%E5%9F%BA%E6%95%B0%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187
基数排序和桶排序也差不多，代码也不好写，他是对数组元素的每一位进行分配，比如就是有0-9范围的10个桶，先按个位进行分配最后拿出来的数组保证个位数上面是有序的，然后再是按十位数进行比较，最后确保十位数上面是有序的，以此类推……为什么先从个位数上开始，我认为个位数对他的影响是相对最小，当十位数上面的数值相同时，比较大小才是再比较个位数上面的数值。如果数组元素都是只含有个位数的话，这感觉又和计数排序一样了，也和桶排序差不多，不过就是分成了十个桶，然后刚好不用再继续排序了，所以这个代码还是要靠数据的信息。
十大排序之间的比较
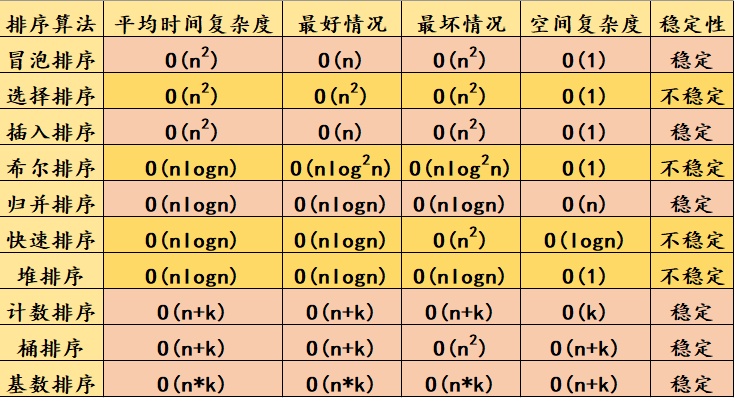
常用十大排序算法_calm_G的博客-CSDN博客https://blog.csdn.net/qq_51664685/article/details/124427443?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169193979216800211581821%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169193979216800211581821&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-2-124427443-null-null.142%5Ev92%5Einsert_down1&utm_term=%E5%8D%81%E5%A4%A7%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187各个排序之间都有自己的优缺点，我记得常用的就是快速排序，归并排序，堆排序这三个，他们三者的平均时间复杂度都比较理想，归并排序就是在时间复杂度理想的情况下还能够保证稳定性，这个还是比较重要的，稳定性我认为的就是按照排序的规则两个含义是一样的情况，不然按照从小到大排序有两个10，这两个10的位置不一样，如果就是表示数字的话那两个的位置就没有什么要求，但是如果还表示其他要求的话，不稳定的排序就可能会导致本来在后面的10移动到前面10的前面；堆排序就是三者后面需要的空间复杂度最少的，而且他最坏情况也是最好的；快速排序其他两个虽然时间复杂度是一样的，但是他的实现速度平均下来还是比其他两个快，但是缺点就是不稳定，而且最坏情况也不理想。
总结
这些排序算法有些事之前还记得，有些是写博客的时候才去找的，因为老师当时讲数据结构的时候讲的比较浅，很多东西都是需要自己去摸索的，借着这个机会做了一下总结，虽然网上有很多人写了，但是自己写的和别人写的总归是有点不一样的。反正这些排序要理解的话，需要按照他的概念，对照这程序每一步都要知道他的含义，包括那些函数的递归他到哪层了，还有就是循环代表的含义是什么。
