307 . 区域和检索 - 数组可修改

在这里插入图片描述

区间和解题思路

这是一道很经典的题目，通常还能拓展出一大类问题。

针对不同的题目，我们有不同的方案可以选择（假设我们有一个数组）：
- 数组不变，求区间和：「前缀和」、「树状数组」、「线段树」
- 多次修改某个数（单点），求区间和：「树状数组」、「线段树」
- 多次修改某个区间，输出最终结果：「差分」
- 多次修改某个区间，求区间和：「线段树」、「树状数组」（看修改区间范围大小）
- 多次将某个区间变成同一个数，求区间和：「线段树」、「树状数组」（看修改区间范围大小）
这样看来，「线段树」能解决的问题是最多的，那我们是不是无论什么情况都写「线段树」呢？

答案并不是，而且恰好相反，只有在遇到第 4 类问题，不得不写「线段树」的时候，我们才考虑线段树。因为「线段树」代码很长，而且常数很大，实际表现不算很好。我们只有在不得不用的时候才考虑「线段树」。
总结一下，我们应该按这样的优先级进行考虑：
- 简单求区间和，用「前缀和」
- 多次将某个区间变成同一个数，用「线段树」
- 其他情况，用「树状数组」

方法：树状数组

树状数组概述

要介绍树状数组，首先引入二叉树：
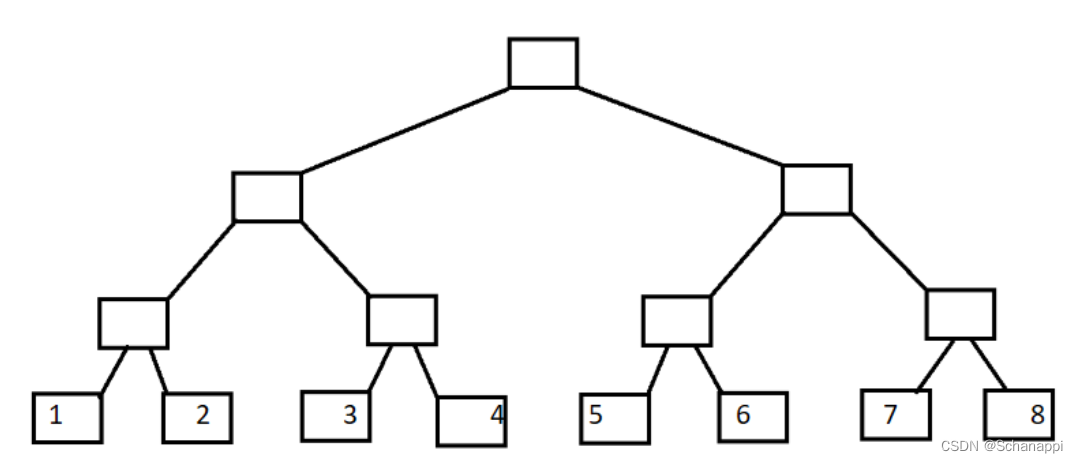
变形一下，就得到了树状数组：

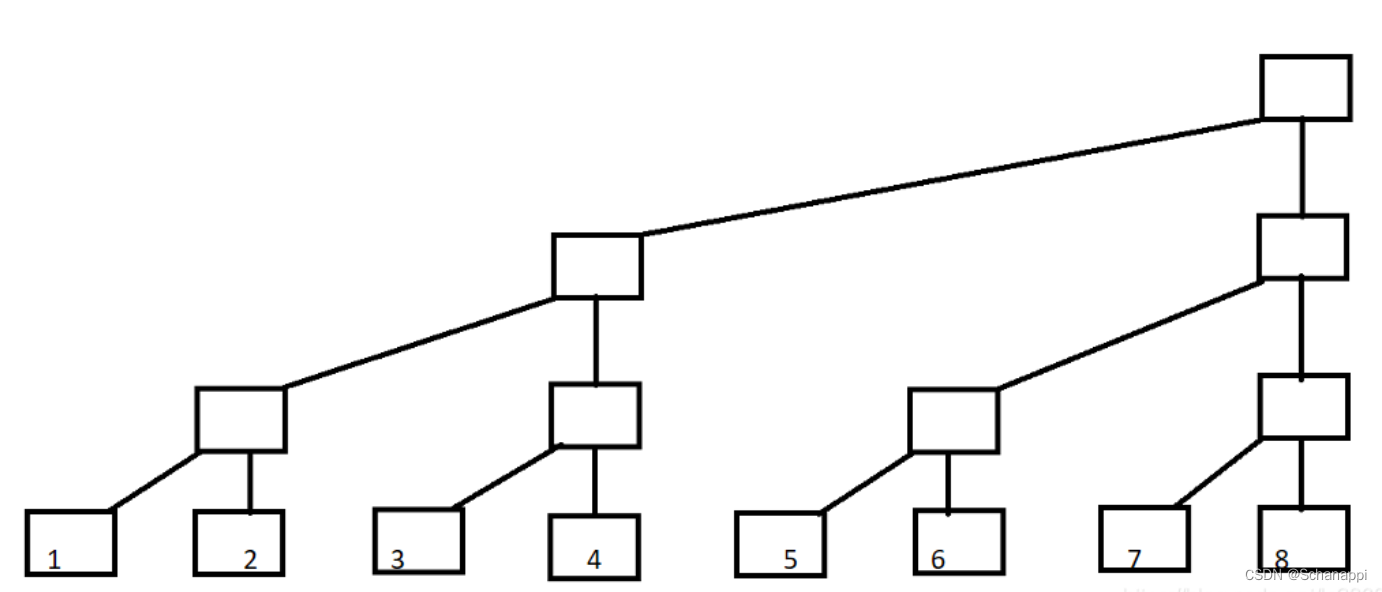
定义树状数组

首先定义一个累加和数组 sums，假设数组有 8 个元素,如图所示,其中 n_i 是原始数据, s_i 是累加和数据：

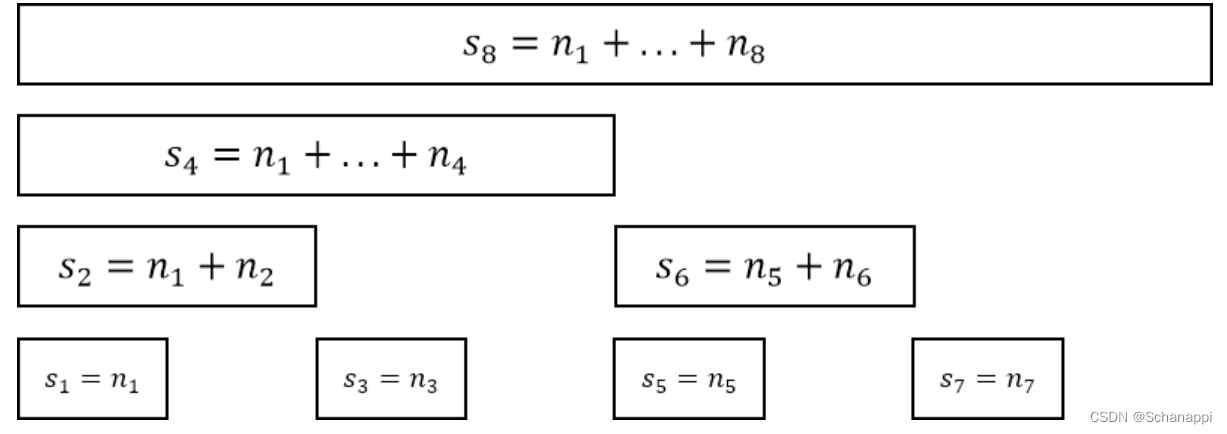
在这里插入图片描述

s[1]=n[1];
s[2]=n[1]+n[2];
s[3]=n[3];
s[4]=n[1]+n[2]+n[3]+n[4];
s[5]=n[5];
s[6]=n[5]+n[6];
s[7]=n[7];
s[8]=n[1]+n[2]+n[3]+n[4]+n[5]+n[6]+n[7]+n[8];

那么我们如何初始化 sums 这个数组呢？

当我们要对 sums[1] 初始化时，也就是加上 nums[1]，而 sums[2]、sums[4]、sums[8] 也都需要加上 nums[1]；

将这几个节点的下标写成二进制：sums[(001)]、sums[(010)]、sums[(100)]、sums[(1000)]

不难发现，sums[(1000)] = sums[(100)] + 4，sums[(100)] = sums[(010)] + 2，sums[(010)] = sums[(001)] + 1，即可以表示成 sums[(y)] = sums[(x)] + C，C 就是 x 最低位数 1 代表的二进制，比如 x = 100 = 4 。

对于上述发现，我们可以使用函数 lowbit(x) 来计算 x 最低位1 所代表的二进制：
```
int lowbit(int x) {
    return x & (-x);
}
```
因此，sums[(y)] = sums[(x)] + lowbit(x)；

当我们对 sums 数组进行初始化的时候，我们就是将所有和 nums[i] 相关联的节点都加上 nums[i]，不断向上操作，直到下标越界。
```
void insert(int index, int val) {
    // 下标+1
    int x = index + 1;
    while (x < sums.size()) {
        sums[x] += val;
        x += lowbit(x); 
    }
}
```

更新树状数组

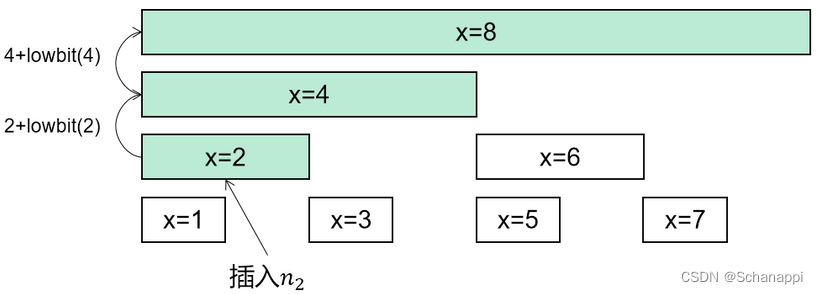
更新操作和初始化类似，都是执行向上操作，使用 x += lowbit(x)来寻找被影响的数组下标。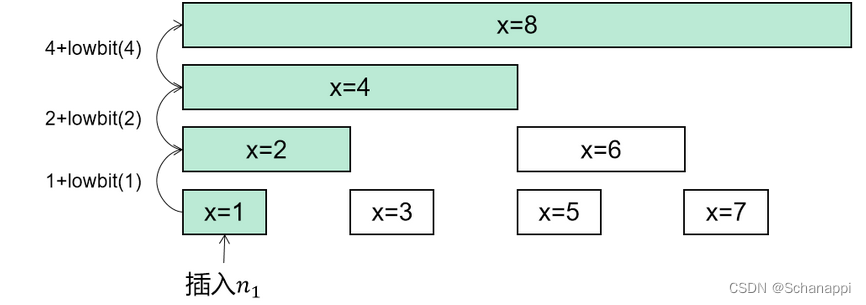

在这里插入图片描述

void update(int index, int val) {
    int x = index + 1;
    while(x < sums.size()) {
        // 减去原先的值，加上新值
        sums[x] = sums[x] - nums[index] + val;
        x += lowbit(x);
    }
    nums[index] = val;
}

查询树状数组

查询是一个向下访问的过程，使用 x -= lowbit(x)来寻找下一个下标。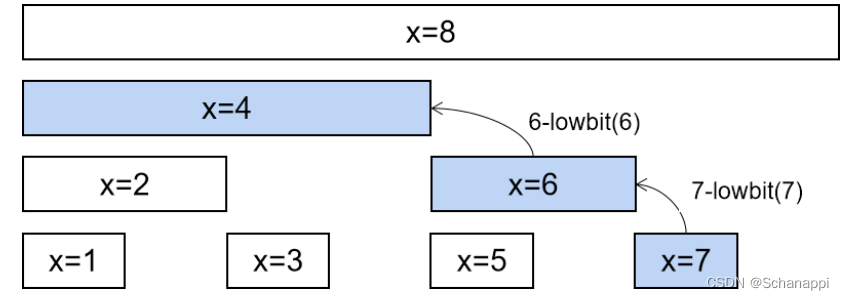

在这里插入图片描述

int query(int x) {
    int ans = 0;
    while(x > 0) {
        ans += sums[x];
        x -= lowbit(x);
    }
    return ans;
}

区间求和

在完成左右端点的前缀和查询后，就可以对区间求和。

int sumRange(int left, int right) {
    return query(right + 1) - query(left);
}

代码

class NumArray {
public:
    vector<int> sums; // 累加和
    vector<int> nums;
    int lowbit(int x){
        return x & (-x);
    }
    // 原数组长度+1, 原因是计算lowbit时,使用下标0会进入死循环
    NumArray(vector<int>& nums) : nums(nums){
        sums.resize(nums.size() + 1);
        for(int i=0; i<nums.size(); ++i){
            // 初始化累加和数组
            update(i, nums[i]);
        }
    }
    void insert(int index, int val) {
        // 下标+1
        int x = index + 1;
        while (x < sums.size()) {
            sums[x] += val;
            x += lowbit(x); 
        }
    }
    void update(int index, int val) {
        int x = index + 1;
        while(x < sums.size()) {
            // 减去原先的值，加上新值
            sums[x] = sums[x] - nums[index] + val;
            x += lowbit(x);
        }
        nums[index] = val;
    }
    
    int sumRange(int left, int right) {
        return query(right + 1) - query(left);
    }
    int query(int x) {
        int ans = 0;
        while(x > 0) {
            ans += sums[x];
            x -= lowbit(x);
        }
        return ans;
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * obj->update(index,val);
 * int param_2 = obj->sumRange(left,right);
 */