给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

 解析：

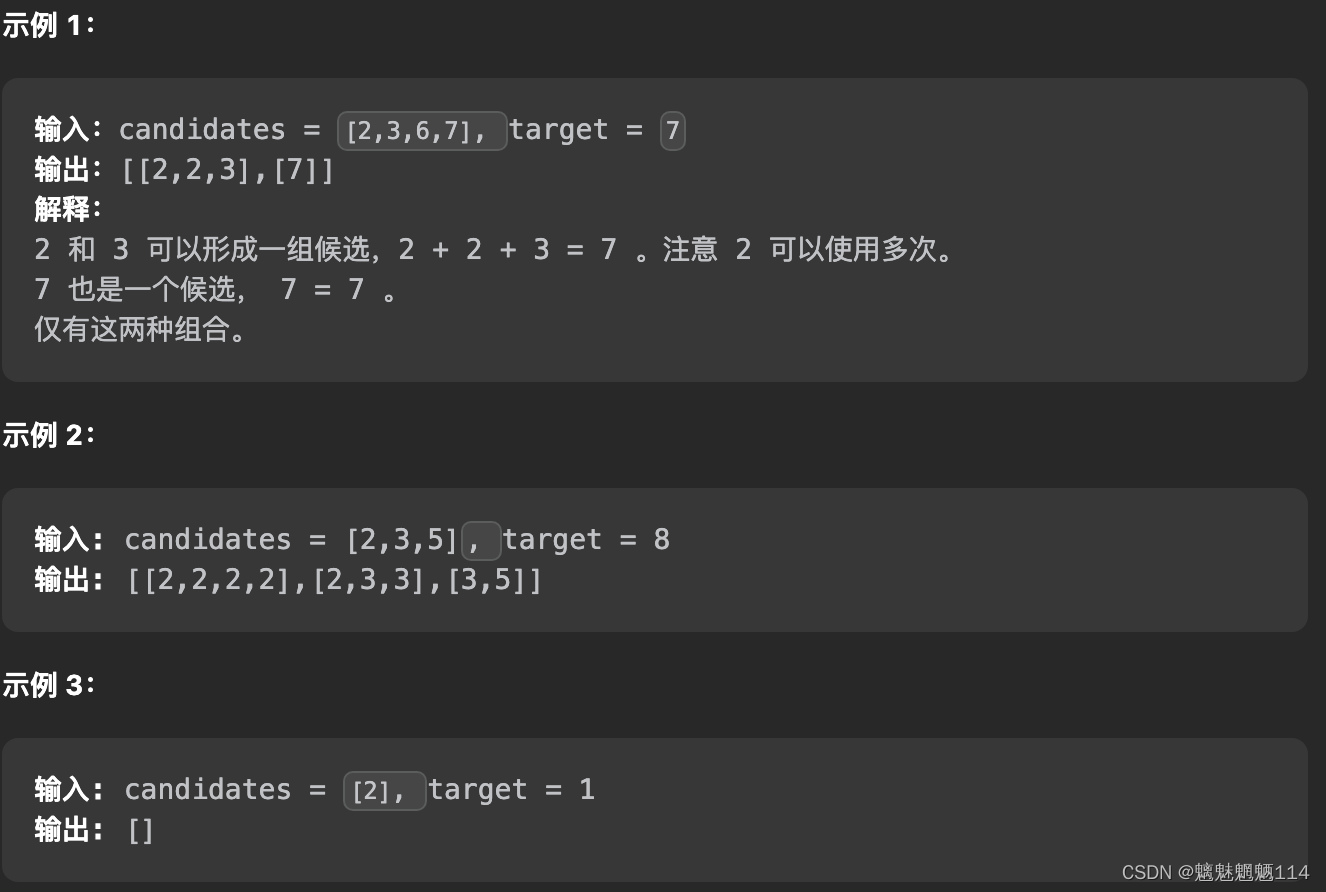
思路分析：根据示例 1：输入: candidates = [2, 3, 6, 7]，target = 7。

候选数组里有 2，如果找到了组合总和为 7 - 2 = 5 的所有组合，再在之前加上 2 ，就是 7 的所有组合；
同理考虑 3，如果找到了组合总和为 7 - 3 = 4 的所有组合，再在之前加上 3 ，就是 7 的所有组合，依次这样找下去。
基于以上的想法，可以画出如下的树形图。建议大家自己在纸上画出这棵树，这一类问题都需要先画出树形图，然后编码实现。

编码通过 深度优先遍历 实现，使用一个列表，在 深度优先遍历 变化的过程中，遍历所有可能的列表并判断当前列表是否符合题目的要求，成为「回溯算法」（个人理解，非形式化定义）。

回溯算法的总结我写在了「力扣」第 46 题（全排列）的题解 《回溯算法入门级详解 + 经典例题列表（持续更新）》 中，如有需要请前往观看。

以输入：candidates = [2, 3, 6, 7], target = 7 为例：

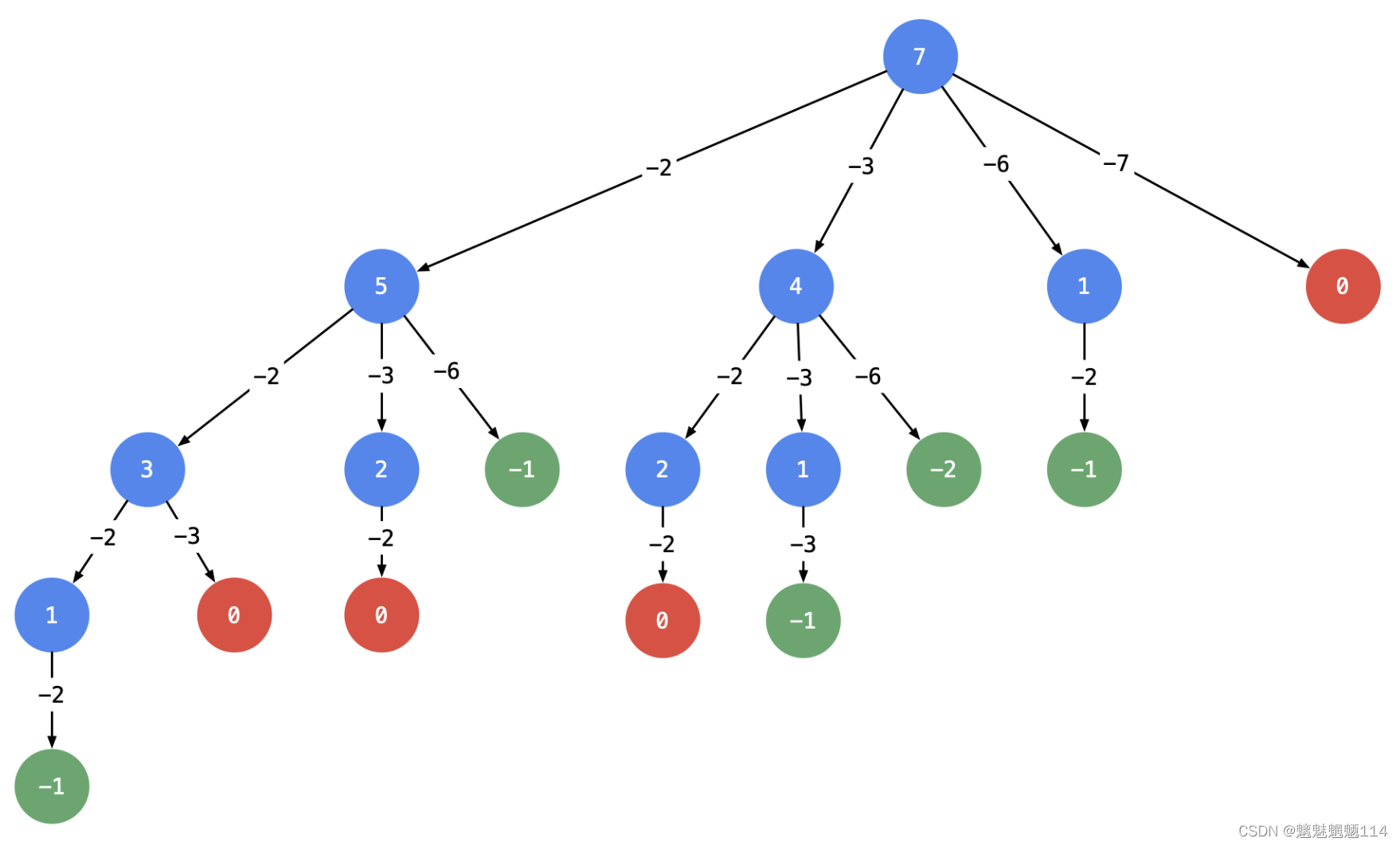
说明：

以 target = 7 为 根结点 ，创建一个分支的时 做减法 ；
每一个箭头表示：从父亲结点的数值减去边上的数值，得到孩子结点的数值。边的值就是题目中给出的 candidate 数组的每个元素的值；
减到 000 或者负数的时候停止，即：结点 000 和负数结点成为叶子结点；
所有从根结点到结点 000 的路径（只能从上往下，没有回路）就是题目要找的一个结果。
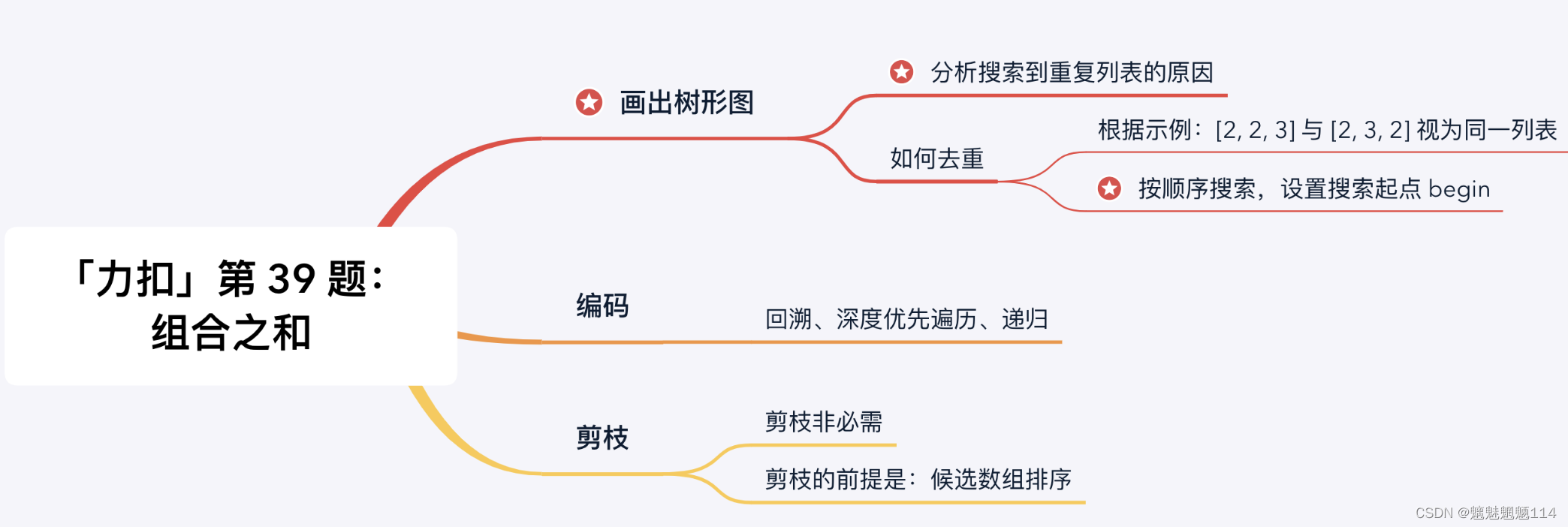
这棵树有 444 个叶子结点的值 000，对应的路径列表是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]]，而示例中给出的输出只有 [[7], [2, 2, 3]]。即：题目中要求每一个符合要求的解是 不计算顺序 的。下面我们分析为什么会产生重复。

产生重复的原因是：在每一个结点，做减法，展开分支的时候，由于题目中说 每一个元素可以重复使用，我们考虑了 所有的 候选数，因此出现了重复的列表。

一种简单的去重方案是借助哈希表的天然去重的功能，但实际操作一下，就会发现并没有那么容易。

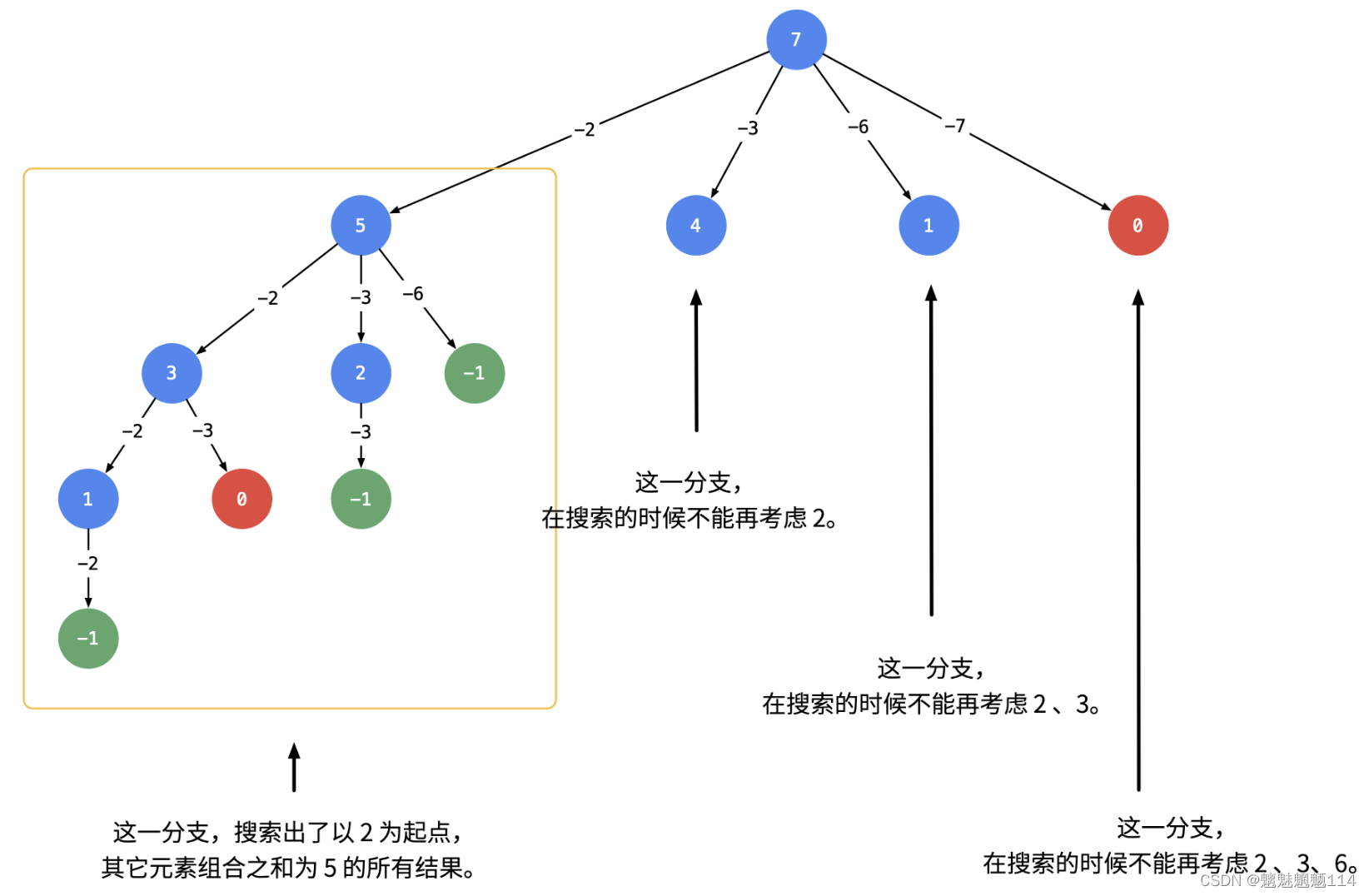
可不可以在搜索的时候就去重呢？答案是可以的。遇到这一类相同元素不计算顺序的问题，我们在搜索的时候就需要 按某种顺序搜索。具体的做法是：每一次搜索的时候设置 下一轮搜索的起点 begin，请看下图。

即：从每一层的第 222 个结点开始，都不能再搜索产生同一层结点已经使用过的 candidate 里的元素。 

 

友情提示：如果题目要求，结果集不计算顺序，此时需要按顺序搜索，才能做到不重不漏。「力扣」第 47 题（ 全排列 II ）、「力扣」第 15 题（ 三数之和 ）也使用了类似的思想，使得结果集没有重复。

剪枝提速
根据上面画树形图的经验，如果 target 减去一个数得到负数，那么减去一个更大的树依然是负数，同样搜索不到结果。基于这个想法，我们可以对输入数组进行排序，添加相关逻辑达到进一步剪枝的目的；
排序是为了提高搜索速度，对于解决这个问题来说非必要。但是搜索问题一般复杂度较高，能剪枝就尽量剪枝。实际工作中如果遇到两种方案拿捏不准的情况，都试一下。

 实现代码

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        if(candidates.length == 0){
            return res;
        }
        //排序是剪枝的前提
        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates,0,target,path,res);
        return res;
    }

    private void dfs(int[] candidates, int begin, int target, Deque<Integer> path, List<List<Integer>> res){
        if(target == 0){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i = begin; i < candidates.length;i++) {
            //重点理解这里的剪枝，前提是数组已经有序
            if(target - candidates[i] < 0){
                break;
            }
            path.addLast(candidates[i]);
            System.out.println("递归之前 => " + path + "，剩余 = " + (target - candidates[i]));

            //由于每一个元素可以重复使用，下一轮搜索的起点依然是i(顺序搜索去重了)
            //如果不能重复使用的滑，i+1
            //如果不去重的话，i=0
            dfs(candidates, i ,target - candidates[i], path ,res);
            //状态重置
            path.removeLast();
            System.out.println("递归之后 => " + path);
        }

    }
}

总结：

什么时候使用 used 数组，什么时候使用 begin 变量
有些朋友可能会疑惑什么时候使用 used 数组，什么时候使用 begin 变量。这里为大家简单总结一下：

排列问题，讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为不同列表时），需要记录哪些数字已经使用过，此时用 used 数组；
组合问题，不讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为相同列表时），需要按照某种顺序搜索，此时使用 begin 变量。
注意：具体问题应该具体分析， 理解算法的设计思想 是至关重要的，请不要死记硬背。

补充说明

如果对于「回溯算法」的理解还很模糊的朋友，建议在「递归」之前和「递归」之后，把 path 变量的值打印出来看一下，以加深对于程序执行流程的理解。

<1递归之前 => [2]，i=0,剩余 = 5
<2递归之前 => [2, 2]，i=0,剩余 = 3
<3递归之前 => [2, 2, 2]，i=0,剩余 = 1
3>递归之后 => [2, 2]，(1-2)<0,break跳出循环dfs执行完，接着执行remove,回溯删除arr[2],递归<3>结束
<4递归之前 => [2, 2, 3]，i=1,重新执行for循环，剩余 = 0,res,add()
4>递归之后 => [2, 2] 接着执行remove,回溯删除arr[2]，递归<4>结束， 3-6<0，剪枝
2>递归之后 => [2] 接着执行remove,回溯删除arr[1] ，递归<2>结束，(5-6)<0,剪枝
<5递归之前 => [2, 3]，剩余 = 2
5>递归之后 => [2] （4-6)<0,剪枝
1>递归之后 => []

-----
<1递归之前 => [3]，剩余 = 4
<2递归之前 => [3, 3]，剩余 = 1
2>递归之后 => [3]
1>递归之后 => []

------
递归之前 => [6]，剩余 = 1
递归之后 => []

--------
递归之前 => [7]，剩余 = 0
递归之后 => []
输出 => [[2, 2, 3], [7]]

参考解题链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台