（一）马氏过程和泊松过程、维纳过程的联系

泊松过程、维纳过程两者都是独立增量过程。独立增量过程是马氏过程的条件：
1. 随机过程是独立增量过程
2. X（0）= 0
满足以上两个条件的随机过程都是马氏过程。

注意：

上述结论的证明通过马氏过程的定义完成，即证明第j个和第n个独立增量相互独立，且该结论用到了第3章第4节的一个重要定理。

从该例题，我们可以得出结论，初始值为0的独立增量随机过程一定是马氏过程，而且x(0) = 0是必要条件，不可或缺。但是反过来，马氏过程不一定是初始值为0的独立增量随机过程。

题目虽然简单，但是理解起来还是有一些深度的。

马氏过程的定义：

P { X n ∣ x n − 1 , x n − 2 , x n − 3 , . . . , x 1 , x 0 } = P { X n , x n − 1 , x n − 2 , x n − 3 , . . . , x 1 , x 0 } P { x n − 1 , x n − 2 , x n − 3 , . . . , x 1 , x 0 } = P { X n ∣ x n − 1 } P\{ X_n | x_{n-1},x_{n-2},x_{n-3},...,x_{1},x_{0}\} = \\ \frac{ P\{ X_n ,x_{n-1},x_{n-2},x_{n-3},...,x_{1},x_{0}\}}{P\{ x_{n-1},x_{n-2},x_{n-3},...,x_{1},x_{0}\} } = P\{ X_n | x_{n-1}\} P{Xn​∣xn−1​,xn−2​,xn−3​,...,x1​,x0​}=P{xn−1​,xn−2​,xn−3​,...,x1​,x0​}P{Xn​,xn−1​,xn−2​,xn−3​,...,x1​,x0​}​=P{Xn​∣xn−1​}

根据上式的定义，由随即变量的独立性可得：
P { X n ∣ x n − 1 , x n − 2 , x n − 3 , . . . , x 1 , x 0 } = P { X n ∣ x n − 1 } P { x n − 2 } P { x n − 3 } . . . P { x 1 } P { x 0 } P\{ X_n | x_{n-1},x_{n-2},x_{n-3},...,x_{1},x_{0}\} = P\{ X_n | x_{n-1}\} P\{x_{n-2}\}P\{x_{n-3}\}...P\{x_{1}\}P\{x_{0}\}\\ P{Xn​∣xn−1​,xn−2​,xn−3​,...,x1​,x0​}=P{Xn​∣xn−1​}P{xn−2​}P{xn−3​}...P{x1​}P{x0​}

（二）均方积分存在条件的个人理解

关于均方积分的定义和性质：

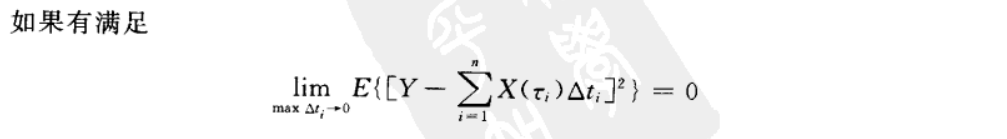
下面简单阐述一下自己对上图中两个结论的理解。

设${\sum }_{i=1}^{n}X({\tau }_i)\Delta t_i=A$，则上图中的均方积分可以化为：

lim ⁡ m a x Δ t i → 0 E { [ Y − ∑ i = 1 n X ( τ i ) Δ t i ] 2 } = E ( Y 2 − 2 A Y + A 2 ) = E ( Y 2 ) + E ( A 2 ) − 2 E ( A Y ) = 0 \lim _{max \Delta t_{i} \to 0}E \{ \biggl [ Y - \sum_{i=1}^{n}X(\tau _{i}) \Delta t_{i} \biggr ] ^{2}\} = \\ E(Y^2 - 2AY + A^2) = E(Y^2) + E(A^2) - 2E(AY) = 0 maxΔti​→0lim​E{[Y−i=1∑n​X(τi​)Δti​]2}=E(Y2−2AY+A2)=E(Y2)+E(A2)−2E(AY)=0
即：
$$E(Y^2)+E(A^2)=2E(AY)$$
从而得出一个满足上述等式的解：A = Y 即：

$$Y=\sum _{i=1}^{n}X({\tau }_i)\Delta t_i={\int }_a^{b}X(\tau )d\tau$$

上图提到，均方积分存在的充分条件是存在：

$${\int }_a^b{\int }_a^{b}X(s)X(t)dsdt={\int }_a^{b}X(s)ds{\int }_a^{b}X(t)dt$$

根据积分的定义，上式的含义是两个原函数在区间[a, b]上的差值的乘积，该差值正好是: $$\sum _{i=1}^{n}X({\tau }_i)\Delta x或者{\int }_a^{b}X(\tau )d\tau$$

因此可以简略的证明，上图中的结论是充分的。