​​​​​​97. Interleaving String

 

72. Edit Distance

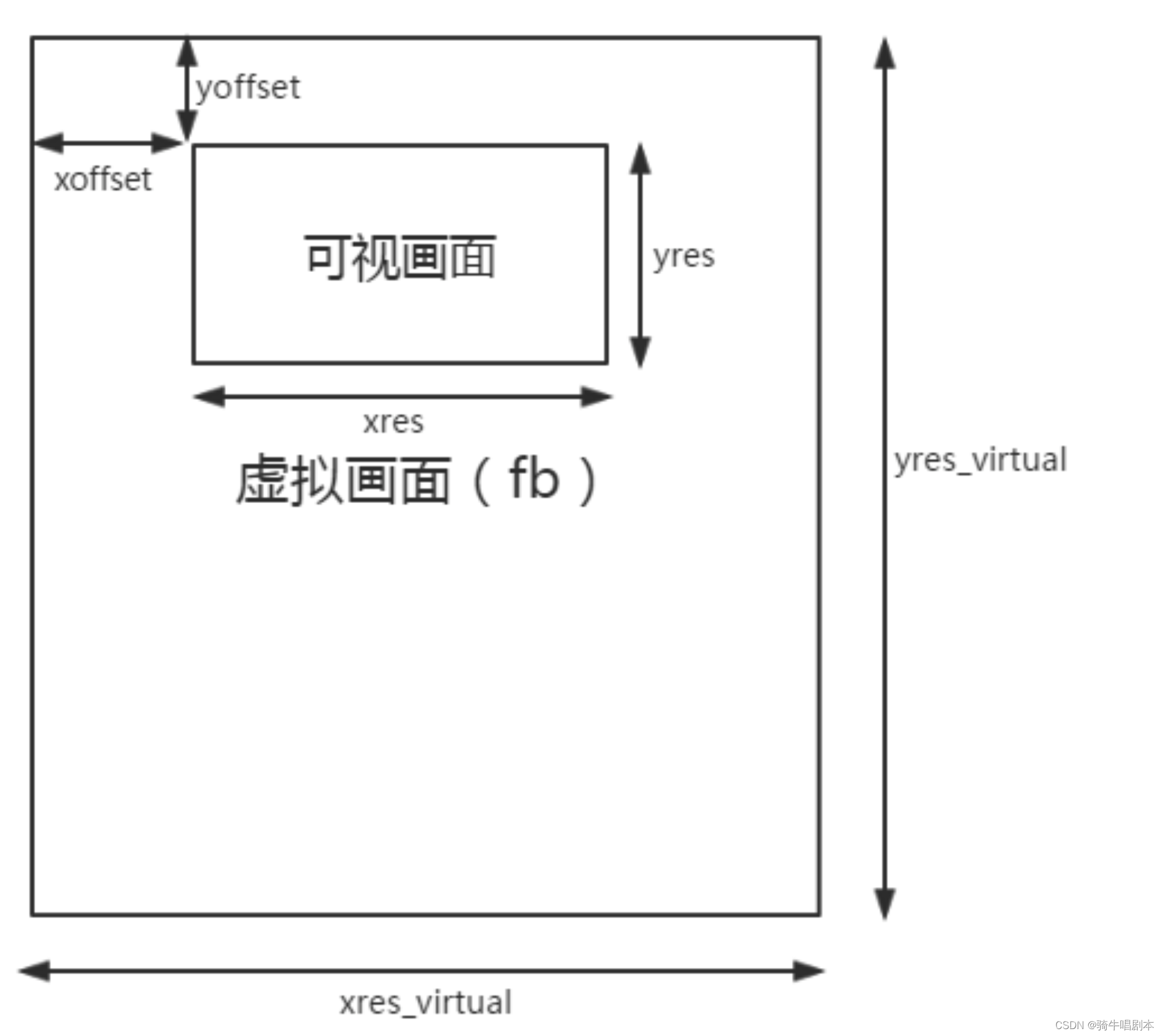
一个bottomup（棋盘从右下角外围逼近[0,0]）如果横轴是string1的index i，纵轴string2的index j，那么，很奇妙的是i和j一起++（从右下角的格子看）的情况，是这两个char一致，共同开始比下一个字符/两个字符不一样但是我们选择replace。那么从右边的格子看，是j++，i不变。这种情况就是insert。j因为找到了一致的char所以++，而i不变因为之前那个不一样的char还是它。那么从下面的格子看，是i++，j不变。正好，是delete的情况，因为delete了也不知道结果是不是match上了，那么j的位置不变，还是和j比，i因为原来的delete了所以是i++。

太神奇了！

每个方格内数字的含义：从该格子开始，到底部/尾部，竖着的怎么match横着的。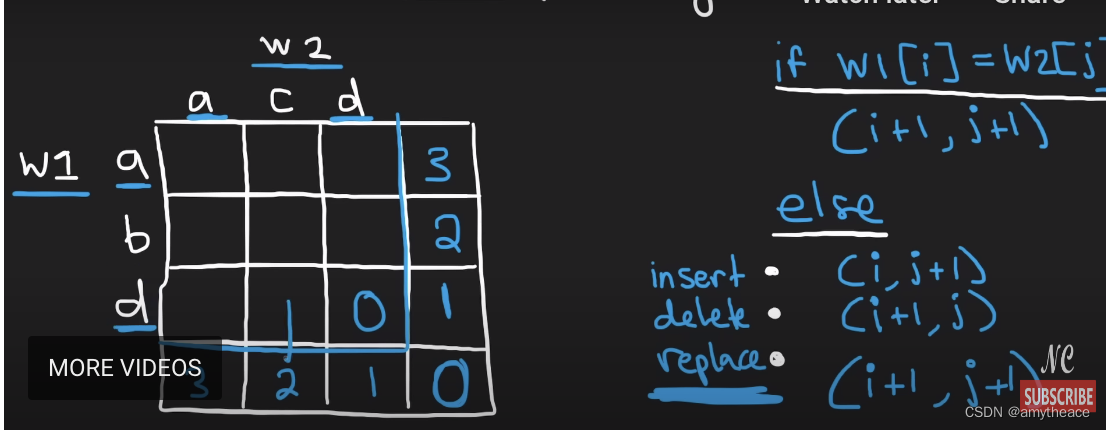

121. Best Time to Buy and Sell Stock

买卖一次

kadane（53，918）：一个求最大连续subarray的专属algorithm。其实就是dp，每个dp[i]都是以array[i]为结尾的最大长度。对于一个新的i，如果dp[i-1]是正的，那么再增加一个就会是以i为结尾最大的（因为dp[i-1]是以i-1为结尾）；如果dp[i-1]是负的，那么以i为结尾最大的就是array[i]。

122. Best Time to Buy and Sell Stock II

买卖无数次

法一：回溯，每天都有是否出手/是否买入的选择，就是一棵树

法二：回溯+memoization，树里面总会有已经计算过的，把这些东西记下来，下会遇到直接用

法三tabulation：还是树的概念

二维dp，dp[i][0]就是当前如果我持有股票最多profit多少，dp[i][1]是当前如果我不持有股票最多profit多少。

持有分为两种情况：原本就持有，继续持有，那么profit不变，如果本来不持有，那么那么代表本次买入新的股票，要花钱，减array[i]。

不持有分为两种情况：本来就不持有，继续不持有，那么profit不变。如果本来持有，本次就不持有了，代表卖了，赚钱了，加array[i]。

每次都记录下这两种情况各最多赚多少

​​​​​​123. Best Time to Buy and Sell Stock III

买卖两次

bidirectional dp。确实很难想到。建立left，right两个dp array，left记录从头开始到该点的最大profit，right记录该点到结尾的最大profit。