力扣刷题 滑动窗口相关的部分题解
- 209. 长度最小的子数组
- 904. 水果成篮
- 76. 最小覆盖子串
209. 长度最小的子数组
leetcode题目链接 209.长度最小的子数组
题目内容是这样的:给定一个含有 n个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0。
理解题意,是要找到这样的连续子数组,满足条件①子数组元素之和≥target;②目标子数组是所有满足条件①的数组中,所含元素个数最少的。 这里强调连续子数组,是因为可能存在题目要求——找到数组中的最少的几个元素,使得元素之和≥target。
寻找连续子数组,可以使用最简单的暴力求解,两遍循环找到答案,时间复杂度O(N^2)。
在暴力求解中,很多子集的寻找是没有必要的,比如下面的情况:子数组[3, 1, 2 ,4]的和已经满足≥target,题意中说明了是正整数数组,那么再往后增加元素,子数组之和会继续增大(一定满足题意),但是子数组的长度也会增大,然而我们的目标是找到满足和≥target的长度最短的子数组。因此在一个子数组之后满足≥target后,固定i,j继续增大是没有必要的。

这道题目可以使用滑动窗口解决,时间复杂度O(N)。思路:
- 1、首先两个指针left和right,分别表示子数组的边界;
- 2、固定left,right向右移动,寻找到和≥target的子数组后停止! ——此时的子数组之和是从nums[left]+……+nums[right],是从左往右累加达到了目标,没有nums[right]子数组的和是<target的,但是没有nums[left]呢?那就不一定啦~ ——因此,接下来就是在这个满足了≥target要求的可行解上,寻找最优解。
- 3、固定right,left向右移动。逐步缩小子数组的长度的同时,验证子数组和是否满足≥target。left一直向右移动,直到子数组和<target,那么此时的left向左一位就是在这个子数组中满足条件的最短的子子数组了。
- 4、此时的left和right之间的数组不满足≥target了,并且在right之前的子数组都探索了,因此重复2-3,遍历完整个数组。
代码如下(C++):
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int n = nums.size();
int ans = INT_MAX;
int start = 0, end = 0, sum = 0;
while(end < n){
sum+=nums[end];
while(sum>=target){
//满足循环要求(题目要求)进入循环,判断当前子数组长度和ans哪个更短,更新
ans = end - start + 1 < ans ? end - start + 1 : ans;
sum -= nums[start];//移除掉start,即left元素,尝试缩短子数组的长度,寻找最优解
start++;
}
end++;//end,即right要一直向右移动到知道sum>=target才会进入下面的循环
}
//注意最后可能没有解,所以子数组长度是0
return ans == INT_MAX ? 0 : ans;
}
};
904. 水果成篮
leetcode题目链接 904. 水果成篮

理解题意:①只有两个篮子,那么就只能采摘两种水果;②选择一棵树开始,比如是fruits[left],那么从这颗树开始,每棵树摘一颗果子,直到遇到第三种果树停止,假设是fruits[right];③要寻找right - left + 1最大(摘得的果子数最多)的情况。
简化题意:只包含两种果树的最长连续子数组。
解题思路(滑动窗口):
- 1、用left、right表示子数组的下标,left=0,right=0;kindleft = fruits[left]表示第一种水果,kindright = fruits[right]表示第二种水果;先固定left不变,right向右移动;
- 2、如果fruits[right]是left~right-1子数组的两种元素之一,即两种水果kindleft、kindright之一,right就继续向右移动;过程中更新ans;
- 3.1、如果如果fruits[right]既不是kindleft也不是kindright,即出现了第三种水果,那么当前的子数组的两个元素应该更新。更新为哪两种呢?①可以肯定的是fruits[right]是一种新水果;②另外一种是fruits[right-1](可能是kindleft也可能是kindright)——因为fruits[right] ≠ kindleft && fruits[right] ≠ kindright,但是fruits[right] =kindleft || fruits[right] = kindright,可以得到fruits[right] ≠ fruits[right-1],而子数组是连续的且只能包含两种元素,因此就是fruits[right] 和 fruits[right-1]。
- 3.2 更新子数组中包含的两种新元素后,新的子数组长度也需要更新,即更新left。left从right-1向左移动,直到找到不等于fruits[right-1]的下标(因为子数组中只能包括两种元素)。
代码(C++):
class Solution {
public:
int totalFruit(vector<int>& fruits) {
//记录子数组下标
int left = 0, right = 0;
//记录两种水果——即子数组中的两种元素
int kindleft = fruits[left], kindright = fruits[right];
//答案——水果数量
int ans = 0;
while(right < fruits.size()){
//right向右移动,如果是left~right-1子数组中的元素,并入子数组
if(fruits[right] == kindright || fruits[right] == kindleft){
ans = max(ans, right - left + 1 );
right++;
}
else{//如果fruits[right]是第三种水果,更新kindleft、kindright
kindright = fruits[right];
left = right - 1;
kindleft = fruits[left];
//更新left,找到并入了新水果品种后的子数组的左边界
while(left>=1 && fruits[left-1] == kindleft) left--;
ans = max(ans, right - left + 1);
}
}
return ans;
}
};
76. 最小覆盖子串
leetcode题目链接 76. 最小覆盖子串
题目内容如下: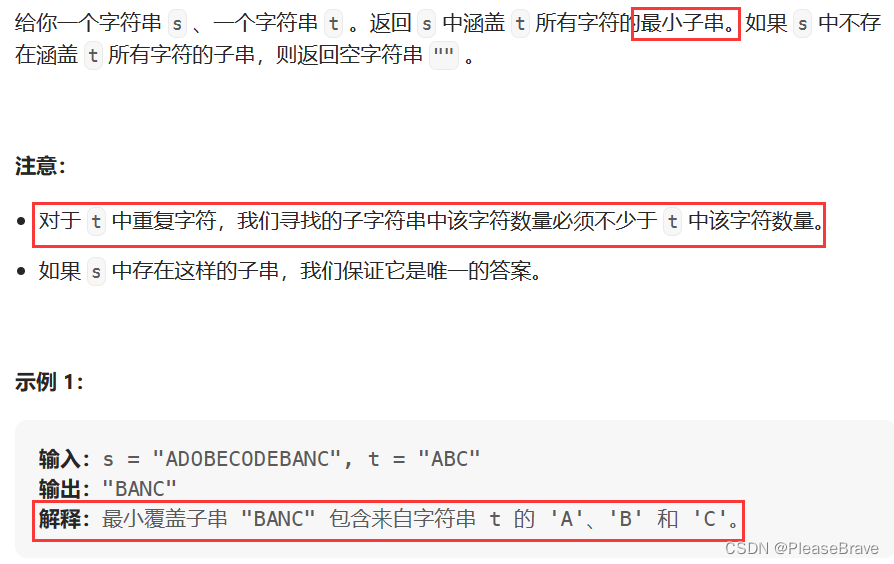
理解题意是寻找s中的最小子串,该子串能够包含t中的全部元素,根据示例可以看出,t中元素的顺序是不重要的;对于重复元素在子串中出现次数不少于在t中重复次数。
问题:在不要求字符顺序的前提下,如果确定子串substring中包含了t中全部元素?—— 对比 字符频数。即统计字符串t中字符及其频数,然后substring更新的过程中也记录子串中包含的t中元素的频数。 直到substring中包含了t中全部元素,并且对应频数≥t中对应元素的频数。 代码实现用distance表示两者差异,substring中新增一个t中的元素时,distance - 1,直到distance = 0,表示子串substring中包含了t中全部元素。
滑动窗口解题思路:
- 1、子串的左右下标用left、right表示。先寻找到一个包含了t中全部元素的子串,固定left,right向右移动。移动过程中如果s[right]是t中元素,那么就统计其频数,如果此时该元素频数已经>t中该元素频数,那么该元素的累积对减少两者的差异没有作用了,即distance不变化;如果该元素的频数 ≤ t中该元素的频数,distance - 1;如果s[right]不是t中元素,直接right++;
- 2、直到distance == 0时,找到了包含t中全部元素的子串,然后在子串中寻找最优解。固定right,left向右移动,left++。如果s[left]是t中元素,删除s[left]后,对应子串中关于s[left]的频数-1,如果减一后 ≥ t中该元素的频数,不会改变此时子串仍然是包含t中全部元素的事实,更新left,同时更新ans;如果如果减一后<t中该元素的频数,那么此时子串与t中元素的差异增加一个,distance++;
- 3、重复1-2,直到遍历完s。
代码如下(C++):
class Solution {
public:
string minWindow(string s, string t) {
int left = 0, right = 0;//记录子串的在S中的左右下标
unordered_map<int,int> T_freq, Sub_freq; //记录t中元素及其频数,记录子串中对应t中元素的频数
int distance = t.size(); //distance表示子串中包含的t中对应元素(及数量)与t的差异
int ans_left = 0, ans_right = s.size() -1; //记录最终目标子串的左右下标
int flage = 0; //记录s中是否存在包括t中全部元素的子串
for(int i = 0; i < t.size(); i++) T_freq[t[i]]++; //统计t中元素及其频数
while(right < s.size()){ //遍历s 先固定left,right向右移动
//如果s[right]是t中的元素,将其统计在子串的频数中
if(T_freq.count(s[right]) != 0){
Sub_freq[s[right]]++;
//如果还没有包含完t中对应元素,那么新增一个s[right],子串和t的差异-1
//如果已经包含了,那么s[right]只是在频数上有累计,但是子串和t的差异不变
if(Sub_freq[s[right]] <= T_freq[s[right]])
distance--;
}
//如果distance=0,即子串中已经包含了t中全部元素,固定right,left向右移动,缩短子串长度寻找最优解
while(!distance){
flage = 1;//一旦distance=0,即存在满足条件的子串,不会返回空串""
//更新结果
if(ans_right - ans_left > right - left) {
ans_right = right;
ans_left = left;
}
//如果删除的s[left]不是t中元素,直接删除,不会影响子串中包含了t中全部元素的事实
//如果删除的s[left]是t中元素
if(T_freq.count(s[left]) !=0 ){
Sub_freq[s[left]]--;//需要更新子串中对应s[left]的频数
//更新频数后可能还是包含t中全部元素的,比如t中a有2个,子串中a有4个,s[left]=a,之后子串中有3个a,但是还是包含了t中全部元素
//如果不能全部包含了,子串和t的差异+1;
if(Sub_freq[s[left]]<T_freq[s[left]])
distance++;
}
left++; //删除s[left]后left右移;
}
right++;
}
if(flage) return s.substr(ans_left , ans_right - ans_left + 1);
else return "";
}
};