在上一篇迪瑞克斯拉算法中将功能实现了出来,完成了图集中从源点出发获取所有可达的点的最短距离的收集。
但在代码中getMinDistanceAndUnSelectNode()方法的实现并不简洁,每次获取minNode时,都需要遍历整个Map,时间复杂度太高。这篇文章主要是针对上一篇文章代码的一个优化。
其优化的过程中主要是用到了加强堆的数据结构,如果不了解的强烈建议先看加强堆的具体实现。
回顾:
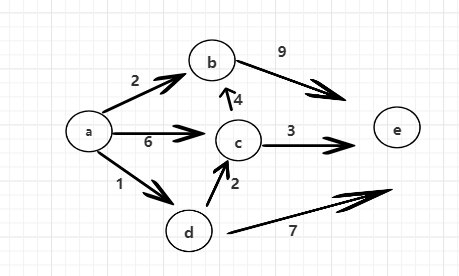
上一篇中,将确定不变的点放入Set中, 每个点之间的距离关系放入Map中,每次遍历Map获取最小minNode,并根据该点找到所有的边,算出最小距离后,放入set中,最终确定最小距离表。
优化
利用加强堆,来维护点和距离的关系,并利用小根堆的优势,让最小的点总是在最上面,需要注意的是,以往的的加强堆中,如果移除了这个元素会直接remove,但是在这里不能remove,因为要记录这个点是否在堆上,是否加入过堆,所以对于确定了的元素,value要改成 -1,用来标记当前元素已经确定,不用再动。
加强堆代码
NodeHeap中的distanceMap用来表示点和距离的关系,根据value的大小动态变化堆顶元素。
主方法是addOrUpdateOrIgnore()。
如果当前元素在堆中并且value != 1(inHeap),说明元素还没有确定,则判断进来的node和value是否大于当前堆中的node对应的value,取小的更新,如果更新,还需要改变元素在堆中位置,因为只可能越更新越小。所以要调用insertHeapify方法去改变堆结构。
如果元素还未加入过堆(!isEntered),则挂在堆尾,并insertHeapify检查是否上移。
pop方法中,如果弹出堆,正常要删除,但是不能删除,除了和最后一个元素交换,下移外,将distanceMap中对应的值改为 -1。否则无法判断该元素是否已经加入过堆,是否已经确定。
public static class NodeHeap {
//Node类型的堆
private Node[] nodes;
//key对应的Node在堆中的位置是value
private HashMap<Node, Integer> heapIndexMap;
//key对应的Node当前距离源点最近距离
private HashMap<Node, Integer> distanceMap;
//堆大小
private int size;
public NodeHeap(int size) {
nodes = new Node[size];
heapIndexMap = new HashMap<>();
distanceMap = new HashMap<>();
this.size = 0;
}
public boolean isEmpty() {
return this.size == 0;
}
public boolean isEntered(Node head) {
return heapIndexMap.containsKey(head);
}
public boolean inHeap(Node head) {
return isEntered(head) && heapIndexMap.get(head) != -1;
}
public void swap(int index1, int index2) {
heapIndexMap.put(nodes[index1], index2);
heapIndexMap.put(nodes[index2], index1);
Node tmp = nodes[index1];
nodes[index1] = nodes[index2];
nodes[index2] = tmp;
}
public void heapify(int index, int size) {
int left = (index * 2) - 1;
while (left < size) {
int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left]) ? left + 1 : left;
smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]) ? smallest : index;
if (smallest == index) {
break;
}
swap(smallest, index);
index = smallest;
left = (index * 2) - 1;
}
}
public void insertHeapify(Node node, int index) {
while (distanceMap.get(nodes[index]) < distanceMap.get((index - 1) / 2)) {
swap(distanceMap.get(nodes[index]), distanceMap.get((index - 1) / 2));
index = (index - 1) / 2;
}
}
public NodeRecord pop() {
NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(0));
swap(0, size - 1);
heapIndexMap.put(nodes[size - 1], -1);
distanceMap.remove(nodes[size - 1]);
heapify(0, --size);
return nodeRecord;
}
public void addOrUpdateOrIgnore(Node node, int distance) {
if (inHeap(node)) {
distanceMap.put(node, Math.min(distanceMap.get(node), distance));
insertHeapify(node, distanceMap.get(node));
}
if (!isEntered(node)) {
nodes[size] = node;
heapIndexMap.put(node, size);
distanceMap.put(node, distance);
insertHeapify(node, size++);
}
}
}
主方法逻辑
上来将给定的点添加到堆中,并且弹出,遍历所有的边放到加强堆中去搞。
public static HashMap<Node, Integer> dijkstra2(Node head, int size) {
NodeHeap nh = new NodeHeap(size);
nh.addOrUpdateOrIgnore(head, 0);
HashMap<Node, Integer> result = new HashMap<>();
while (!nh.isEmpty()) {
NodeRecord record = nh.pop();
Node cur = record.node;
int distance = record.distance;
for (Edge edge : cur.edges) {
nh.addOrUpdateOrIgnore(edge.to, distance + edge.weight);
}
result.put(cur, distance);
}
return result;
}