AtCoder Beginner Contest 314

news2024/11/26 12:46:41

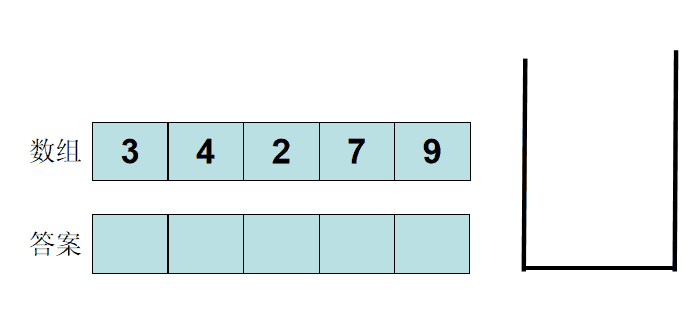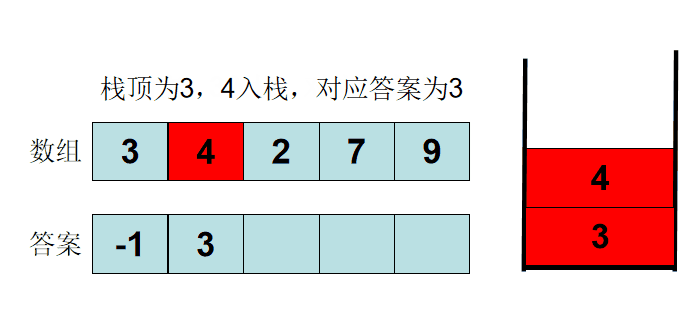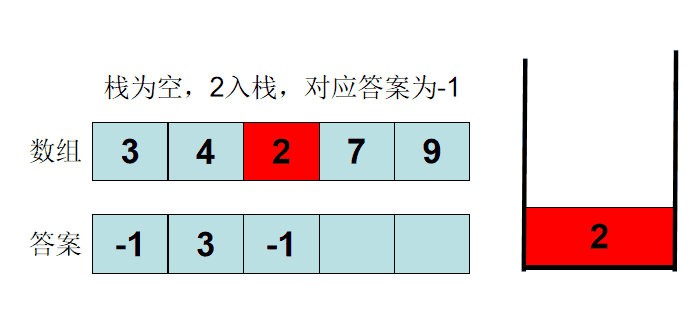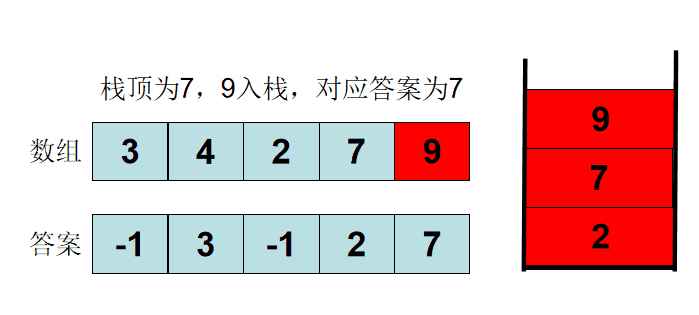
A.直接模拟就行

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
#define int long long
int n,m;
string s="3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679";

void solve(){
    cin>>n;
    n+=2;
    for(int i=0;i<n;i++)
    {
        cout<<s[i];
    }
}

signed main(){
    cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);
    int t=1;
    //cin>>t;
    while(t--) solve();
}

B.直接模拟算次数排序

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
int n,m;
vector<int> a[N];
int cnt[N];
void solve()
{
    cin>>n;
    int mx=0;
    for(int i=1;i<=n;i++)
    {
        cin>>m;
        mx=max(mx,m);
        a[i].push_back(0);
        for(int j=1;j<=m;j++)
        {
            int x;
            cin>>x;
            a[i].push_back(x);
        }
    }
    
    int x;
    cin>>x;
 
    vector<PII> res;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<a[i].size();j++)
        {
            int m=a[i].size();
            if(a[i][j]==x)
            {
                cnt[j]++;
                res.push_back({m-1,i});
                break;
            }
        }
    }
    if(res.size()==0){
        cout<<0;
        return ;
    }
    sort(res.begin(),res.end());
    x=res[0].first;
    vector<int> b;
    for(int i=0;i<res.size();i++)
    if(x==res[i].first) b.push_back(res[i].second);
    sort(b.begin(),b.end());
    cout<<b.size()<<"\n";
    for(auto x:b) cout<<x<<" ";
}

signed main(){
    cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);
    int t=1;
    //cin>>t;
    while(t--) solve();
}

C.把当前颜色集合掏出来全部往右移动即可

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
#define int long long
int n,m;
int a[N];
char b[N];
vector<char> res[N];

void solve(){
    cin>>n>>m;
    string s;
    cin>>s;
    s="?"+s;
    vector<int> cntt(N,0);
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        b[a[i]]=s[i];
        res[a[i]].push_back(s[i]);
    }
    
    for(int i=1;i<N;i++)
    {
        if(b[i])
        {
            res[i].pop_back();
            res[i].push_back(b[i]);
            reverse(res[i].begin(),res[i].end());
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        if(!cntt[a[i]]){
            cout<<b[a[i]];
            cntt[a[i]]++;continue;
        }
        cout<<res[a[i]].back();
        res[a[i]].pop_back();
    }

}

signed main(){
    cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);
    int t=1;
    //cin>>t;
    while(t--) solve();
}

记录一下最后操作是大写还是小写还是没变化，然后顺便记录一下最后操作

因为大小写过后只是单纯改变字母，所以还要存一下后面的操作

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
#define int long long
int n,m;

void solve(){
    string s;
    cin>>n>>s;
    s="?"+s;
    cin>>m;
    int now=-1;
    vector<pair<int,char>> a;
    for(int i=1;i<=m;i++)
    {
        int op,x;char y;
        cin>>op>>x>>y;
        if(op==1){
            s[x]=y;
            a.push_back({x,y});
        }
        else if(op==3)
        {
            now=3;
            a.clear();
        }
        else now=2,a.clear();
    }
    
    if(now==-1)
    {
        for(int i=1;i<=n;i++)
        cout<<s[i];
        return ;
    }
    else if(now==3)
    {
        for(int i=1;i<=n;i++)
        s[i]=(char)(toupper(s[i]));
        for(int i=0;i<a.size();i++){
            int x=a[i].first;char y=a[i].second;
            s[x]=y;
        }
    }
    else{
        for(int i=1;i<=n;i++)
        s[i]=(char)(tolower(s[i]));
        for(int i=0;i<a.size();i++){
            int x=a[i].first;char y=a[i].second;
            s[x]=y;
        }
    }
            for(int i=1;i<=n;i++)
        cout<<s[i];
}

signed main(){
    cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);
    int t=1;
    //cin>>t;
    while(t--) solve();
}

E：首先期望dp

当前m分所需要花费的最小期望，每次枚举操作哪个数组

有个问题就是如果存在0，我一直递归同一个值会wa

所以把3/4*dp[i]=cj+1/4*f[i+4]+1/4*f[i+6]+1/4*f[i+8]

然后每个数乘4/3即可

#include<bits/stdc++.h>
using namespace std;
const int N = 110,mod=998244353;

typedef long long LL;
typedef pair<int, int> PII;

int n,m,k;
vector<int> a[N];

double c[N];


signed main(){
    cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);
  
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>c[i];
        int x;
        cin>>x;
        int zero=0;
        for(int j=1;j<=x;j++)
        {
            int p;cin>>p;
            if(p) a[i].push_back(p);
            else ++zero;
        }
        c[i]=1.0*c[i]*x/(x-zero);
    }
    vector<double> f(m+10,-1);
     function<double(int)> dfs=[&](int m)->double{
        if(m<=0) return 0;
        if(f[m]>=0) return f[m];  
        f[m]=1e18;
        for(int i=1;i<=n;i++)
        {
            double tmp=c[i];
            int sz=a[i].size();
            for(auto j:a[i])
            {
                tmp+=(j>=m?0:dfs(m-j))*(1.0/sz);
            }
            f[m]=min(f[m],tmp);
        }
        return f[m];
    };
    cout << fixed << setprecision(10) << dfs(m) << '\n';
}

假设进行j场比赛，答案就是j场每场赢得概率相加

暴力就是每次合并一个集合，在这个集合全部数加上当前场赢得概率，复杂度n^2超时

但是最后会合并成一个集合，所以我们最后拓扑排序一下，把当前点的概率叠加在子节点的身上即可，子节点就是小于等于n

#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;

int n,m,k;
int a[N],b[N];
int fact[N],infact[N];
vector<PII> g[N];
int qmi(int a,int k,int p){
    int res=1;
    while(k){
        if(k&1) res=(LL) res*a%p;
        a=(LL)a*a%p;
        k>>=1;
    }
    return res;
}
void init(){
    fact[0]=infact[0]=1;
    for(int i=1;i<N;i++){
        fact[i]=(LL)fact[i-1]*i%mod;
        infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod;
    }
}
int C(int a,int b){
    if(b<0||b>a) return 0;
    return ((LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
class dsu {
  public:
    vector<int> p;
    vector<int> sz;
    int n;
 
    dsu(int _n) : n(_n) {
        p.resize(n);
        sz.resize(n);
        iota(p.begin(), p.end(), 0);
        fill(sz.begin(), sz.end(), 1);
    }
 
    inline int get(int x) { return (x == p[x] ? x : (p[x] = get(p[x]))); }
 
    inline bool unite(int x, int y) {
        x = get(x);
        y = get(y);
        if (x != y) {
            p[x] = y;
            sz[y] += sz[x];
            return true;
        }
        return false;
    }
};
signed main(){
    cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);
    init();
    cin>>n;
    dsu d(2*n+10);
    int idx=n;
    for(int i=n+1;i<=n*2;i++)
    d.sz[i]=0;
    for(int i=1;i<n;i++)
    {
        int u,v;cin>>u>>v;
        ++idx;
        int fu=d.get(u),fv=d.get(v);
        int szu=d.sz[fu],szv=d.sz[fv];
        int zonhe=qmi(szu+szv,mod-2,mod);
        g[idx].emplace_back(fu,1ll*szu*zonhe%mod);
        g[idx].emplace_back(fv,1ll*szv*zonhe%mod);
        d.unite(u,idx);
        d.unite(v,idx);
    }
    vector<int> ans(n+10,1);
    function<void(int,int)> dfs=[&](int u,int p){
        if(u<=n)
        {
            ans[u]=p;
            return ;
        }  
        for(auto [v,w]:g[u]){
            dfs(v,(p+w)%mod);
        }
    };
    dfs(idx,0);
    for(int i=1;i<=n;i++)
     cout<<ans[i]<<" \n"[i==n];
    
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/872687.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！