回归拟合：

分类

本文是作者的预测算法系列的第四篇，前面的文章中介绍了BP、SVM、RF及其优化，感兴趣的读者可以在作者往期文章中了解，这一篇将介绍——极限学习机

过去的几十年里基于梯度的学习方法被广泛用于训练神经网络，如BP算法利用误差的反向传播来调整网络的权值.然而，由于不适当的学习步长，导致算法的收敛速度非常慢，容易产生局部最小值，因此往往需要进行大量迭代才能得到较为满意的精度．这些问题，已经成为制约其在应用领域发展的主要瓶颈.

Huang等人［1］ 提出了一种简单高效的单隐层前馈神经网络学习算法，称为极限学习机(extremelearning machine,ELM).其典型优势是训练的速度非常快，具有训练速度快、复杂度低的优点，克服了传统梯度算法的局部极小、过拟合和学习率的选择不合适等[2]问题,目前被广泛地应用于模式识别、故障诊断、机器学习、软测量等领域。

00目录

1 标准极限学习机ELM

2 代码目录

3 ELM的优化实现

4 源码获取

5 展望

参考文献

01 标准极限学习机ELM

1.1 ELM原理

给定一数据集：T={(x1,y1),…,(xl,yl)}，其中xi∈Rn，y∈R，i=1,…,l；含有 N 个隐层节点，激励函数为 G 的极限学习机回归模型可表示为：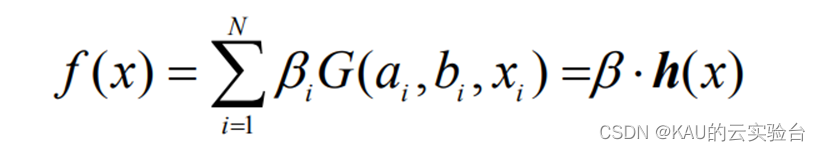

其中：bi 为第 i 个隐层节点与输出神经元的输出权值；ai为输入神经元与第 i 个隐层节点的输入权值；bi为第 i 个隐层节点的偏置；h(x)=[G(a1,b1,x1),…,(aN,bN,xN)]称为隐层输出矩阵。并且ai,bi在训练开始时随机选择，且在训练过程中保持不变。输出权值可以通过求解下列线性方程组的最小二乘解来获得：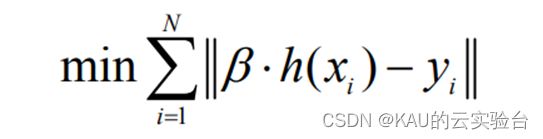

该方程组的最小二乘解为：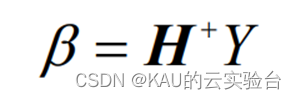

其中， H+称为隐层输出矩阵H的 Moore-Penrose 广义逆.

1.2 ELM优化

由于 ELM 随机给定输入权值矩阵和隐含层偏差，由1.1节中的计算式可知输出权值矩阵是由输入权值矩阵和隐含层偏差计算得到的，可能会存在一些输入权值矩阵和隐含层偏差为 0，即部分隐含层节点是无效的． 因此在某些实际应用中，ELM 需要大量的隐含层节点才能达到理想的精度． 并且 ELM 对未在训练集中出现的样本反应能力较差，即泛化能力不足。针对以上问题可利用优化算法和极限学习机网络相结合的学习算法，即利用优化算法优化选择极限学习机的输入层权值和隐含层偏差，从而得到一个最优的网络[3].

对于ELM优化，以PSO优化ELM为例，其流程如下所示：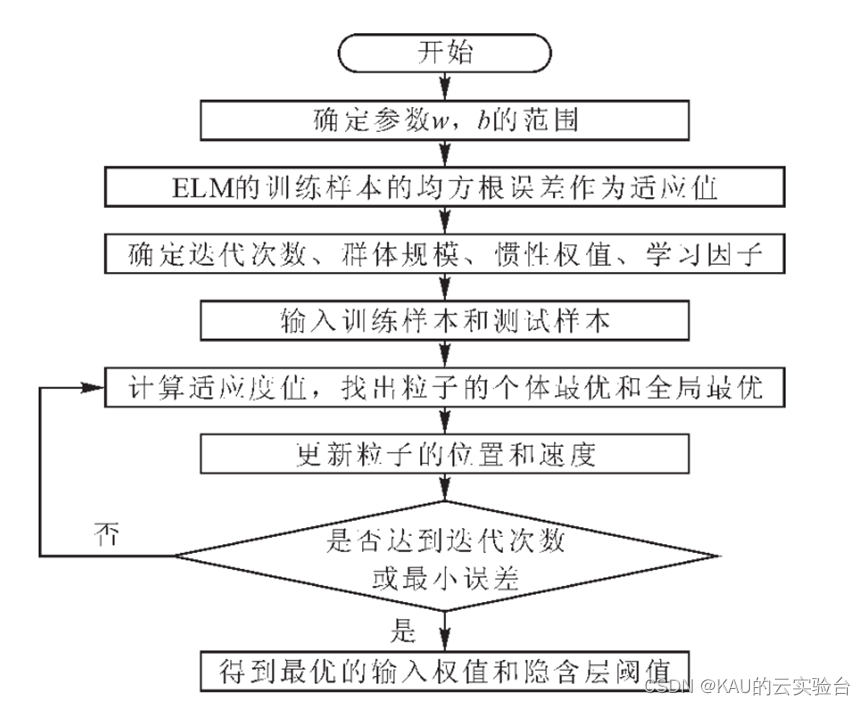

02 代码目录

本文以改进的动态多种群粒子群算法优化ELM，并与标准粒子群算法优化ELM和ELM算法进行对比。

改进的动态多种群粒子群优化算法（IDM-PSO）

分类问题：

其中，IDM_PSO_ELM.m、MY_ELM_CLA.m和PSO_ELM.m都是可独立运行的主程序.而result.m可用于对比这三个算法的效果，若想对比算法，单独运行这个程序即可。

部分源码如下：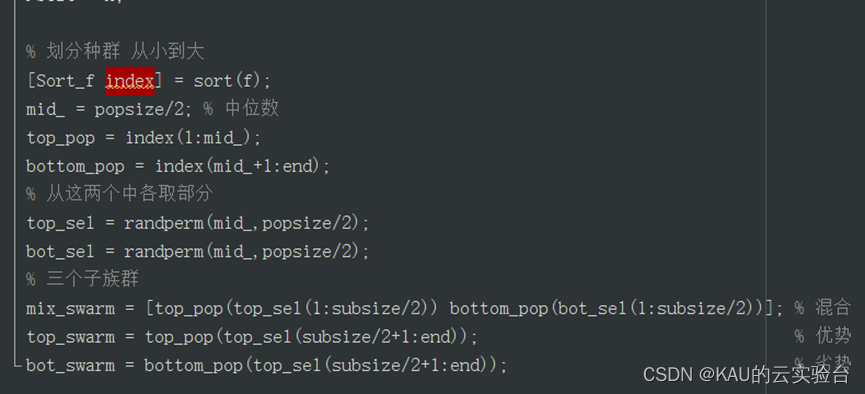

回归拟合问题：

回归拟合的程序和分类的类似，这里不再重复。

部分源码：

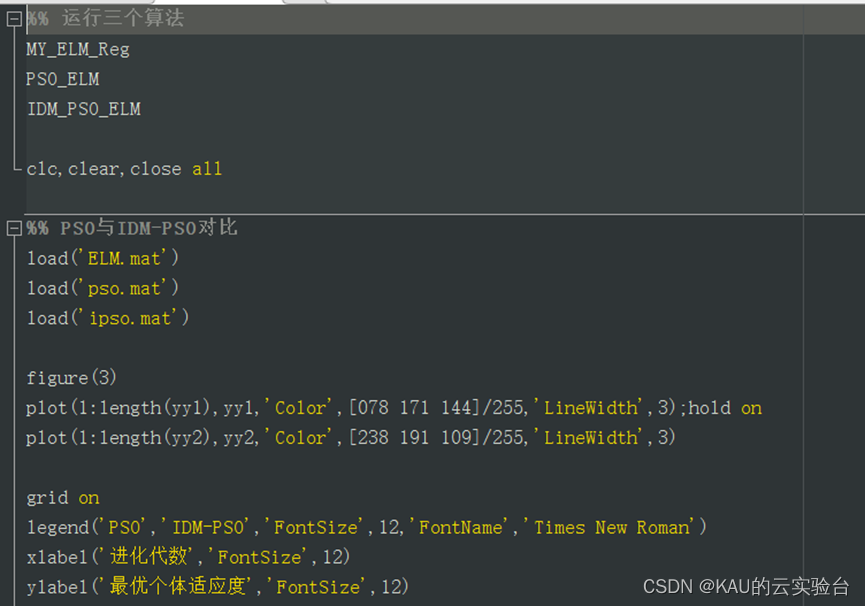
03 极限学习机及其优化的预测结果对比

3.1 回归拟合

应用问题为多输入单输出问题。

3.1.1 评价指标

为了验证所建模型的准确性和精度，分别采用均方根差(Root Mean Square Error，RMSE) 、平均绝对百分误差( Mean Absolute Percentage Error，MAPE)和平均绝对值误差( Mean Absolute Error，MAE) 作为评价标准。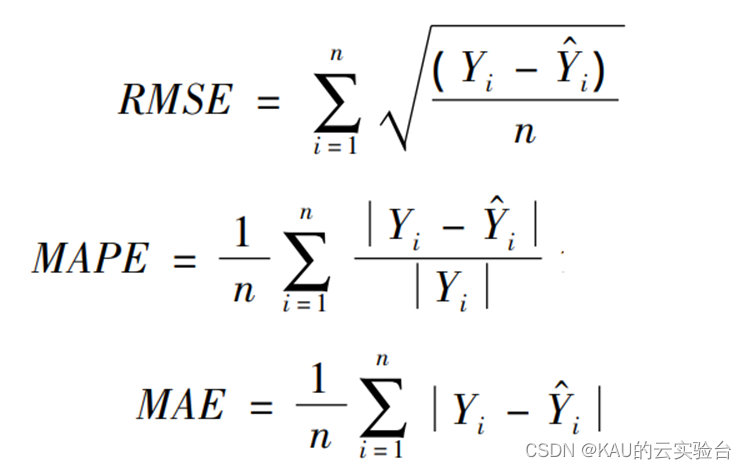

式中 Yi 和Y ^ i分别为真实值和预测值; n 为样本数。

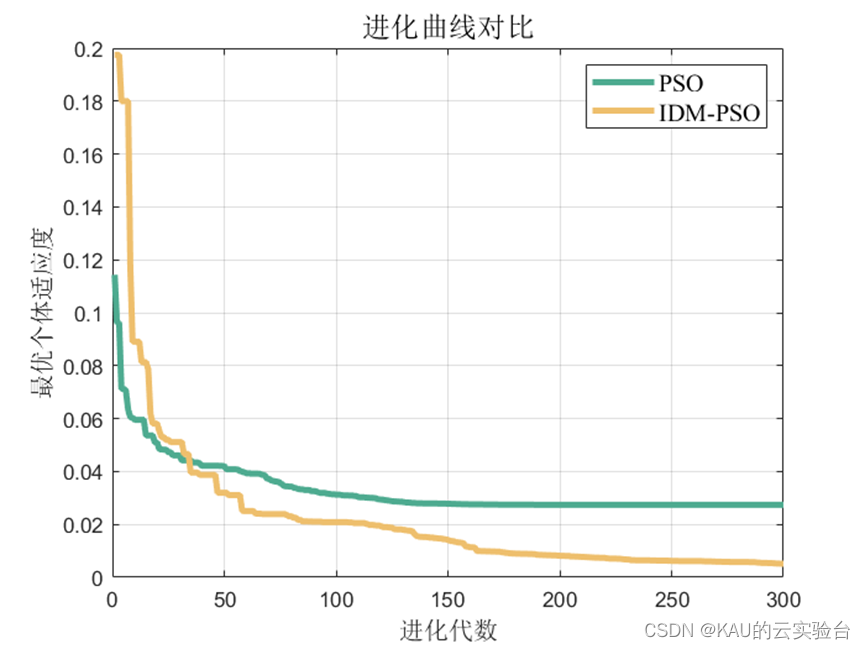
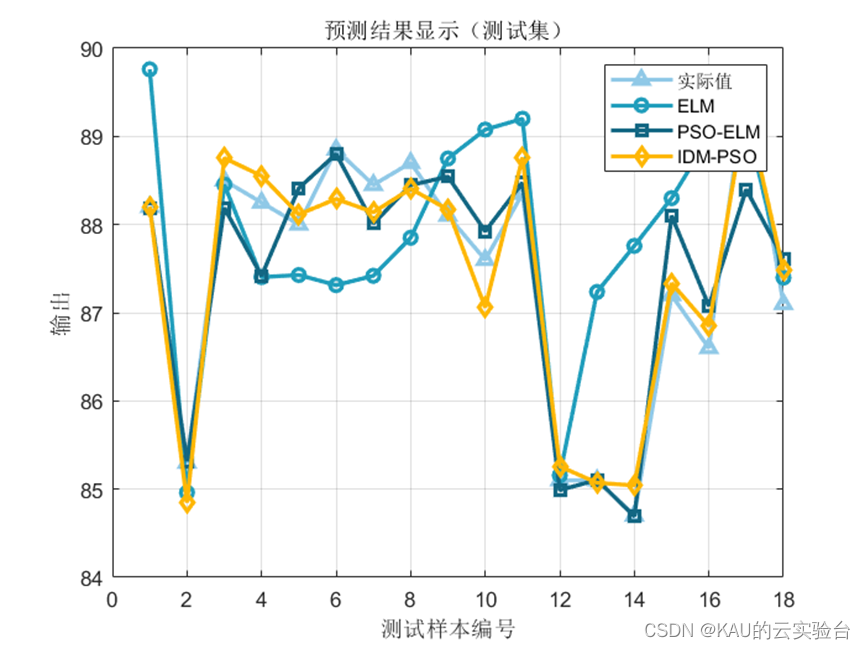
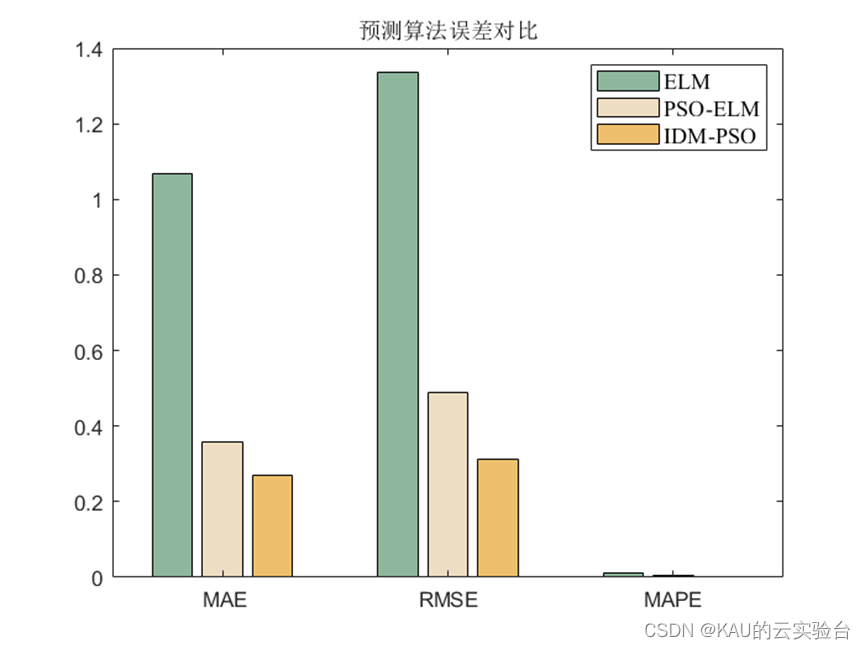
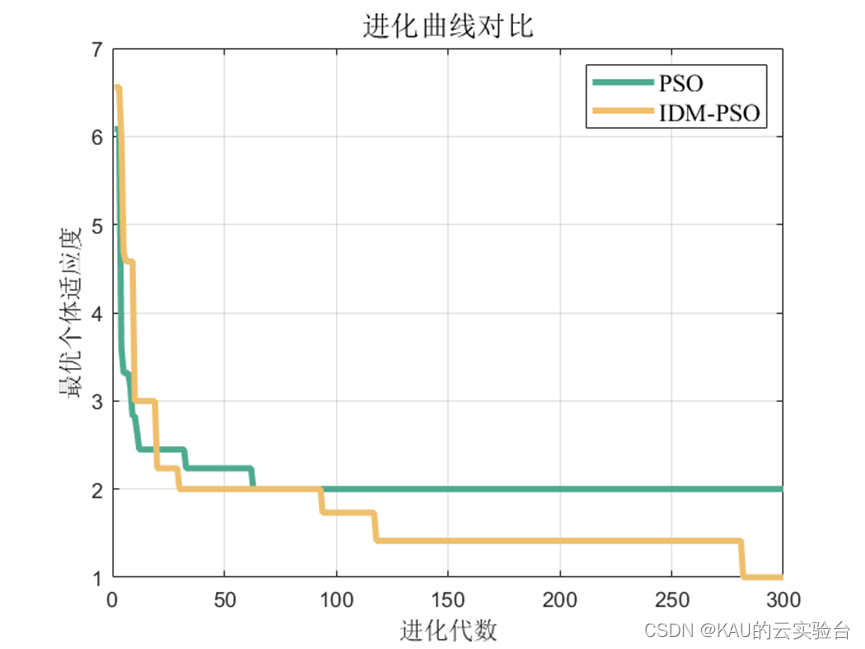
3.1.2 仿真结果

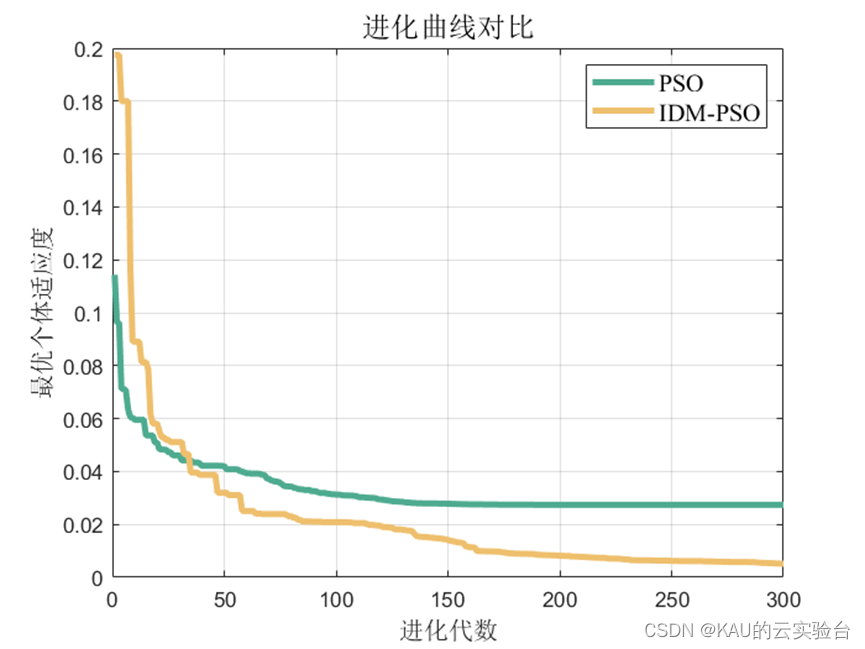
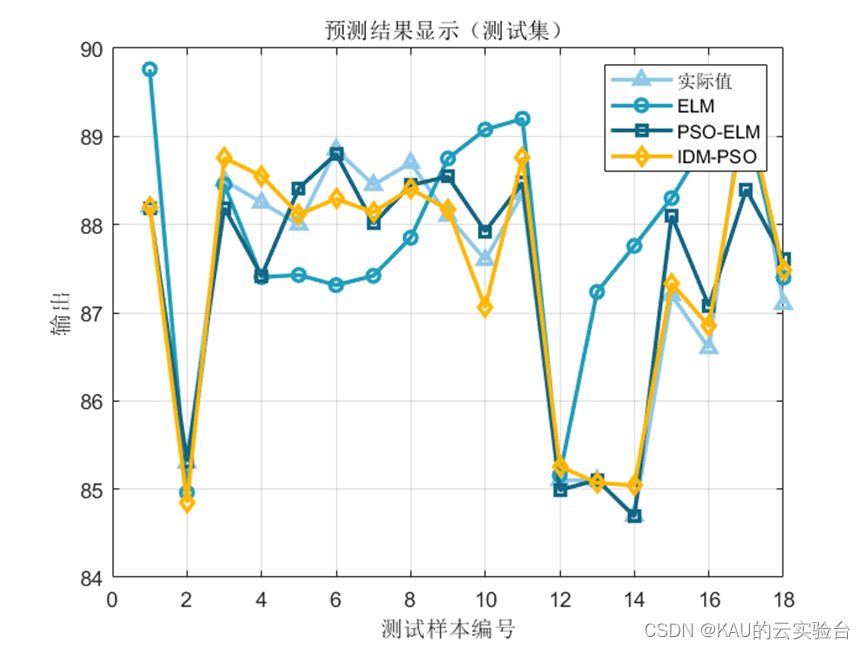
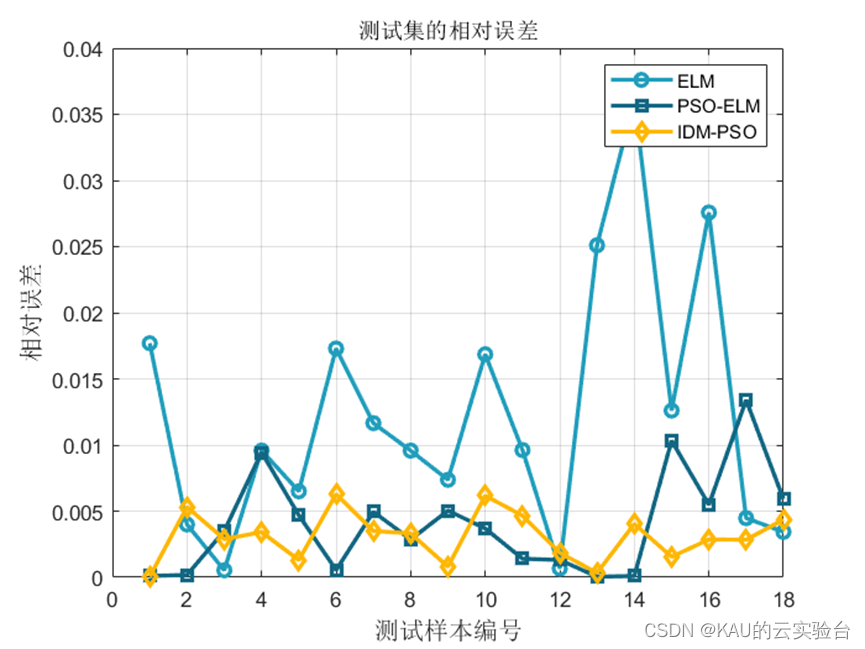
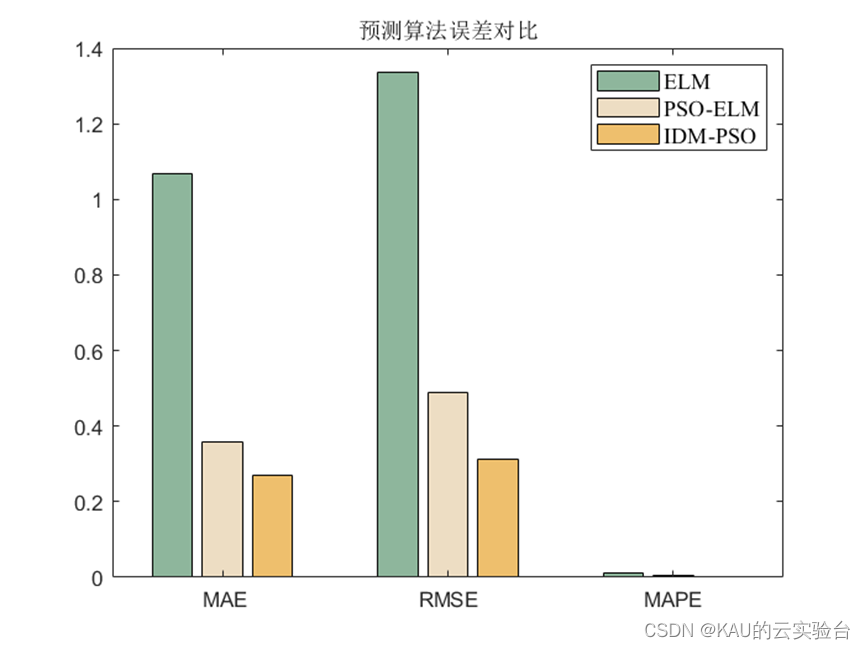
可以看出，优化是有效的。

3.2 分类

3.2.1 评价指标

为验证模型准确率，本文从混淆矩阵、准确率、精确率、召回率、F1-score这些方面进行衡量。

1、混淆矩阵

混淆矩阵是一种可视化工具，混淆矩阵的每一列代表的是预测类别，其总数是分类器预测为该类别的数据总数，每一行代表了数据的真实类别，其总数是该类别下的数据实例总数。主对角线的元素即为各类别的分类准确的个数，通过混淆矩阵能够直观地看出多分类模型的分类准确率。

2、准确率

最为简单判断 SVM 多分类效果的方法就是用以下公式进行准确率r 的计算

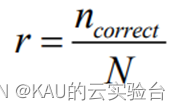
其中 ncorrect代表正确分类的样本个数， N代表测试集中的样本总数。

3、精确度

精度计算的是正类预测正确的样本数，占预测是正类的样本数的比例，公式如下

其中，TP表示的是正样本被预测为正样本的个数，FP表示的是负样本被预测为 正样本的个数。

4、召回率

召回率计算的是预测正类预测正确的样本数，占实际是正类的样本数的比例，公式如下：

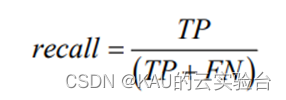
其中， FN 表示的是正样本被判定为负样本的个数。

5、F1-score

F1- score是精度和召回率的调和平均值， F1- score越高说明模型越稳健，计算公式为

6、宏平均（macro-averaging）

宏平均（macro-averaging）是指所有类别的每一个统计指标值的算数平均值， 也就是宏精确率（macro - precision），宏召回率（ macro -recall ），宏 F1 值 （macro- F1 score），其计算公式如下：

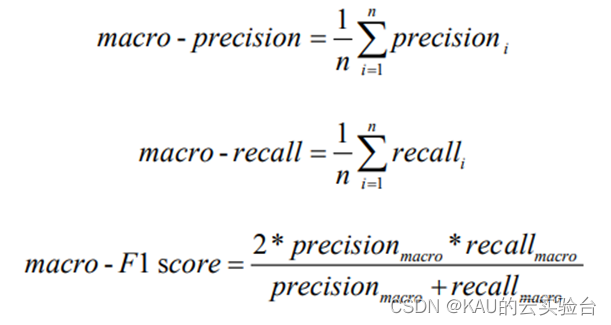
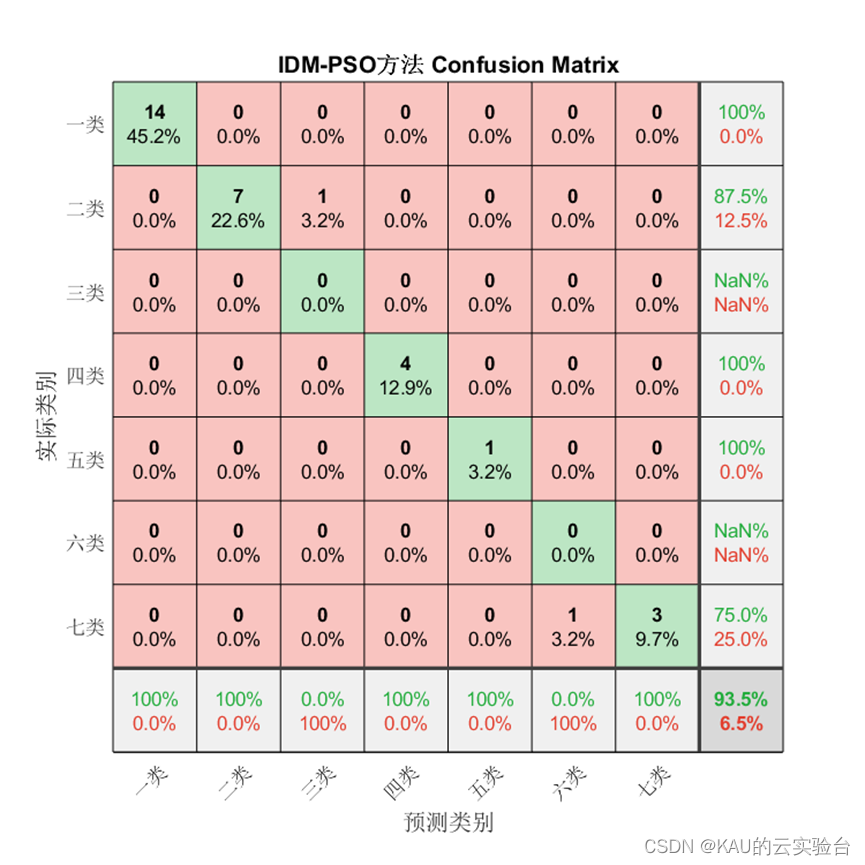
3.2.2 仿真结果

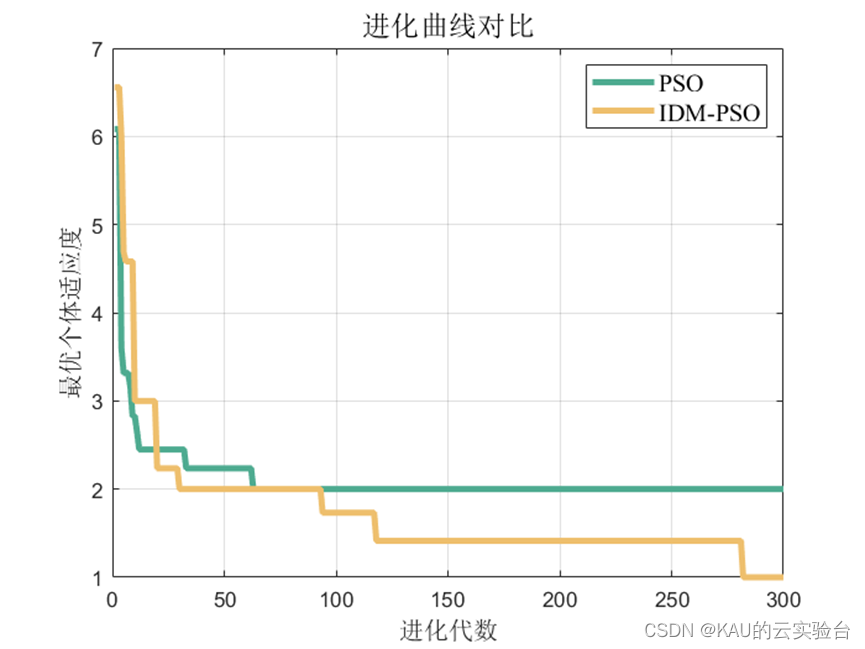
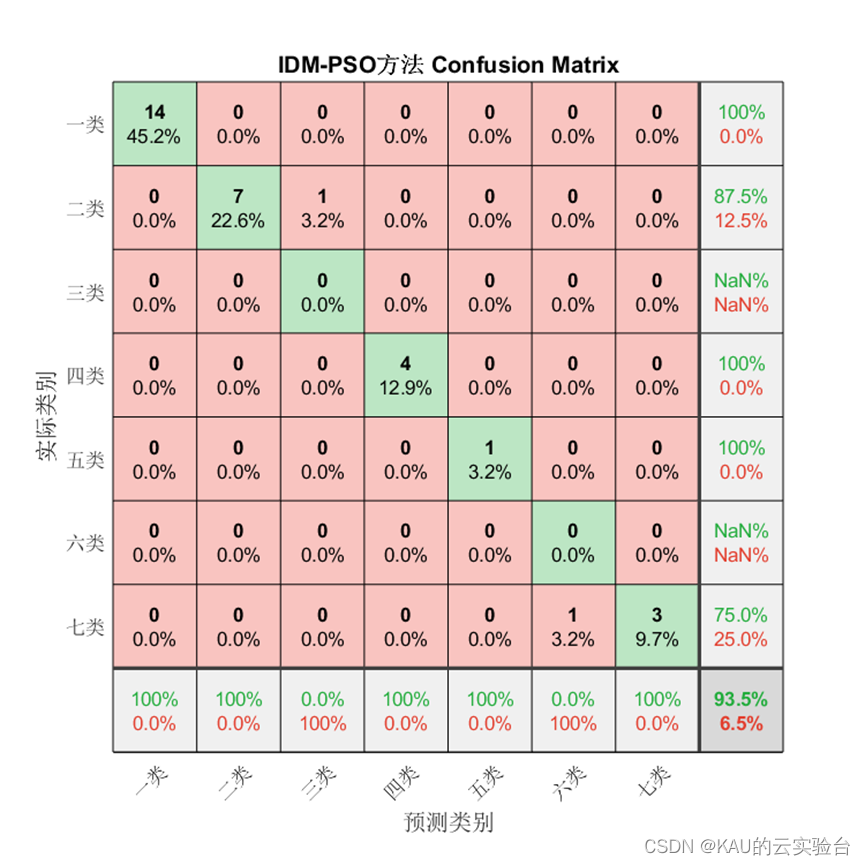
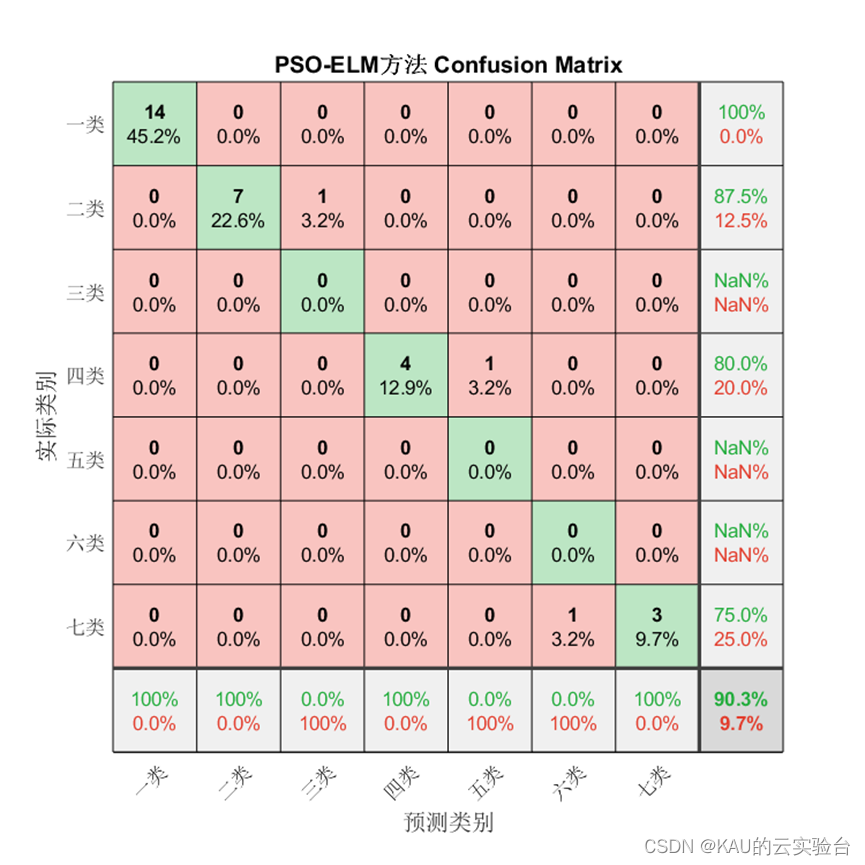
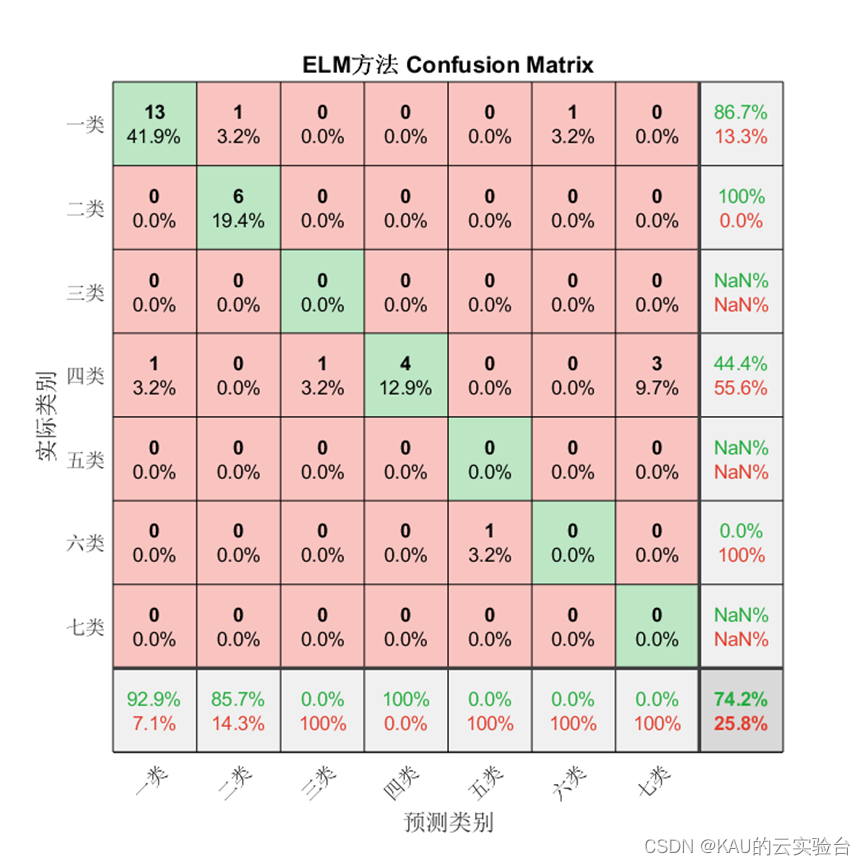
对于分类问题仍然有效，需要注意的是因为某些类别并没有存在预测值，因此由精确率和F1的计算式可知会出现NaN。

04 源码获取

关注作者或私信

05 展望

本文介绍了应用改进的动态多种群粒子群算法优化ELM的案例，同样也可以采用作者前面提到过的麻雀算法等，同时，极限学习机因其在处理大规模数据时出现的无法收敛等问题，出现了核极限学习机、多核极限学习机、深度极限学习机等变体，作者后续也会更新这些算法的实现。

参考文献

[1]Huang G B，Zhu Q Y，Siew C K. Extreme learning machine:A new learning scheme of feedforward neural networks//Proceedings of the 2004 1EEE International Joint Conferenceon Neural Networks. Budapest，Hungary，2004:985-990

[2]FAN Shu-ming,QIN Xi-zhong,JIA Zhen-hong,et al.Time series forecasting based on ELM improved layered ensemble architecture[J].Computer Engineering and Design,2019,40(7):1915-1921.

[3]王杰,毕浩洋.一种基于粒子群优化的极限学习机[J].郑州大学学报(理学版),2013,45(01):100-104.

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞(ง •̀_•́)ง(不点也行)，若有定制需求，可私信作者。