坚持看完,结尾有思维导图总结
这里写目录标题
- 归并排序的思路
- 归并算法的图解
- 具体程序
- 对性质的分析
- 归并排序的非递归版本
- 总结
归并排序的思路
首先第一个问题是,什么是归并排序?
官方的说法: 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法
即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并
按照我的理解
就是首先,先把数组按照一半一半的方式切分(我把这个一半的数组叫做半数组),先把半数组有序排列,然后再利用两个有序数组的合并合并出原来的有序数组
归并排序的思路是什么?
按照定义中我的理解
这个问题可以进一步划分为
1.大数组如何拆成两个数组?
2.如何得到有序数组?
3.两个有序数组是如何合并的?
通过分析可以知道
一个大数组,假设数组元素是这样
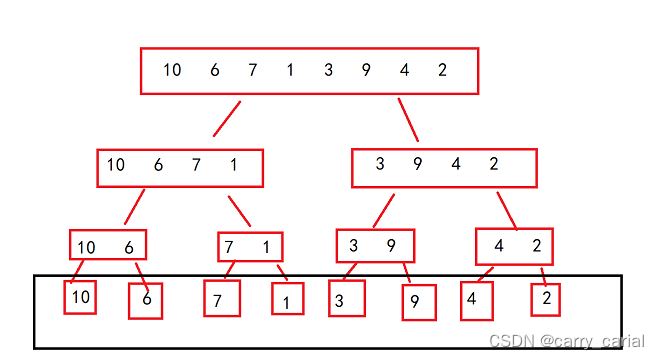
通过分解,能够回答第 1 ,2 个问题
如果每次都取到数组中间位置,就能够将数组进行切分,所以我们要得到中间位置
当将数组切分到最小数组,每个数组中只有一个元素的时候,这个数组天然就是有序的
第三个问题,当得到最小的区间的时候,就能够进行单趟的排序
单趟的排序就是要进行两个有序数组的合并
有序数组的合并的思路是:
1.两个有序数组的元素依次比较,将小的元素先放进临时数组中
2.任意一个数组走完的时候,剩下的其余元素全部放进临时数组内
3.将临时数组拷贝回原数组

归并算法的图解

需要注意的是:
原数组a 下标和tmp 的下标是一致的
具体程序
void _mergesort(int*a ,int begin,int end,int* tmp)
{
int mid = begin + (end-begin)/2;
//切分终止
if(begin >= end)
{
return ;
}
//切分数组
_mergesort(a,begin,mid,tmp);
_mergesort(a,mid+1,end,tmp);
//单趟有序数组合并
int begin1 = begin,end1 = mid;
int begin2 = mid+1,end2 = end;
int j = begin;
while(begin1<=end1 && begin2<=end2)
{
if(a[begin1] <= a[begin2])
{
//小的放在tmp 上,并且保持稳定
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while(begin1<=end1)
{
tmp[j++] = a[begin1++];
}
while(begin2<=end2)
{
tmp[j++] = a[begin2++];
}
//拷贝回原数组
memcpy(a+begin,tmp+begin,sizeof(int)*(end-begin+1));
}
void MergeSort(int*a,int len)
{
int* tmp = (int*)malloc(len*sizeof(int));
if(tmp == NULL)
{
exit(-1);
}
_mergesort(a,0,len-1,tmp);
free(tmp);
tmp = NULL;
}
对性质的分析
这里主要解决几个问题
1.归并算法的时间复杂度,空间复杂度
2.归并算法的稳定性
由于归并排序是二叉树结构,递归深度为 logn
每次排序为 n 次
所以时间复杂度为 n*logn
空间复杂度 为 n
额外开辟的空间为 n
递归深度使用空间为 logn
稳定性,稳定
因为每次单趟排序,当数字相等时,默认使用第一个数组(即前数组)的数据
所以相同数据的顺序没有被打乱,因此是稳定的
归并排序的非递归版本
第一个问题,非递归的版本如何实现?
上面我们使用递归,把数组拆分
从大数组变成了元素个数为1的有序数组
然后再利用有序数组合并完成单趟排序
如果我们能过手动控制数组元素的个数
从一个,到两个,到四个的有序数组合并,就能实现归并排序的非递归方式
对应的图解就是

这里需要提出一个问题
在这里设定的 grip 可以看成每个子数组的元素个数
begin1 ,end1 是 第一个子数组的开始和结束
begin2,end2是 第二个自数字的开始和结束
除了 begin1 是第一个元素,其余的 end1,begin2,end2都是由 begin 和 grip 计算出来的
end1 ,begin2,end2 就会有越界的可能
就需要进行讨论
end1 越界和 begin2 都是说明数组2不存在,可以跳过本次排序,直接进行下一次排序
end 2越界则说明数组2的结束需要调整,调整为原数组的结束
对应的程序为
void MergeSortNonR(int* a, int len)
{
int* tmp = (int*)malloc(sizeof(int) * len);
if (tmp==NULL)
{
exit(-1);
}
int begin, end, begin1, end1, begin2, end2, grip;
grip = 1;
//当 grip 超过 len 的时候结束
while (grip < len)
{
//单趟
for (int i = 0; i < len; i += grip)
{
//begin end 是归并后的数组的头尾,
//begin1 ,end1 是 第一个子数组的开始和结束,
//begin2,end2是 第二个自数字的开始和结束
begin = begin1 = i;
end1 = begin1 + grip - 1;
begin2 = end1 + 1;
end = end2 = begin2 + grip - 1;
//前两种数组2不存在的情况直接进行下一次排序
if (end1 > len-1 || begin2 > len-1)
{
break;
}
if (end2 > len-1)
{
end2 = end = len-1;
}
//单趟归并
int j = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
//拷贝
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
grip *= 2;
}
free(tmp);
tmp = NULL;
}
总结
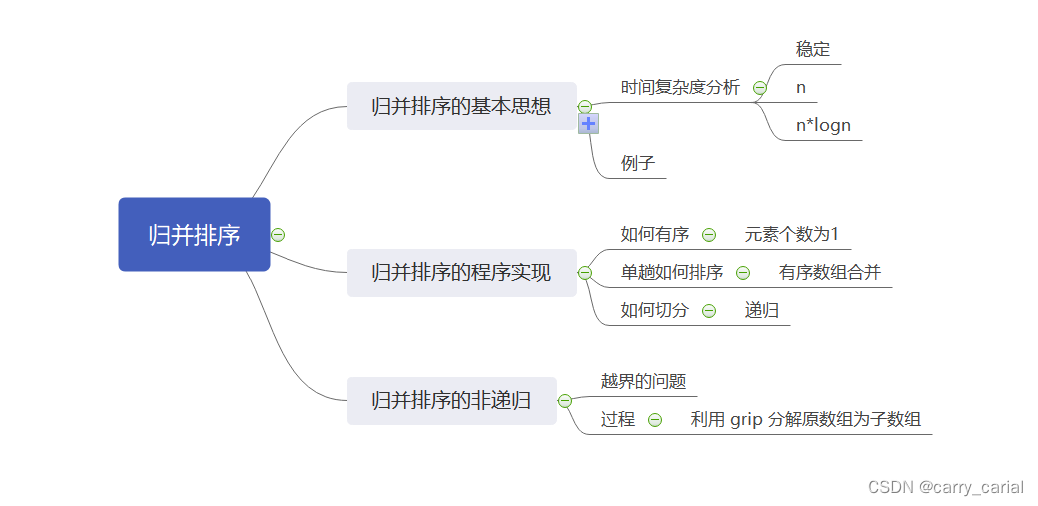
希望大家看完,能够有所收获
如果有错误,请指出我一定虚心改正
动动小手点赞
鼓励我输出更加优质的内容

![[激光原理与应用-53]:《激光焊接质量实时监测系统研究》-4-激光焊接系统软件设计](https://img-blog.csdnimg.cn/61218c58769a4948be184f50b294810f.png)