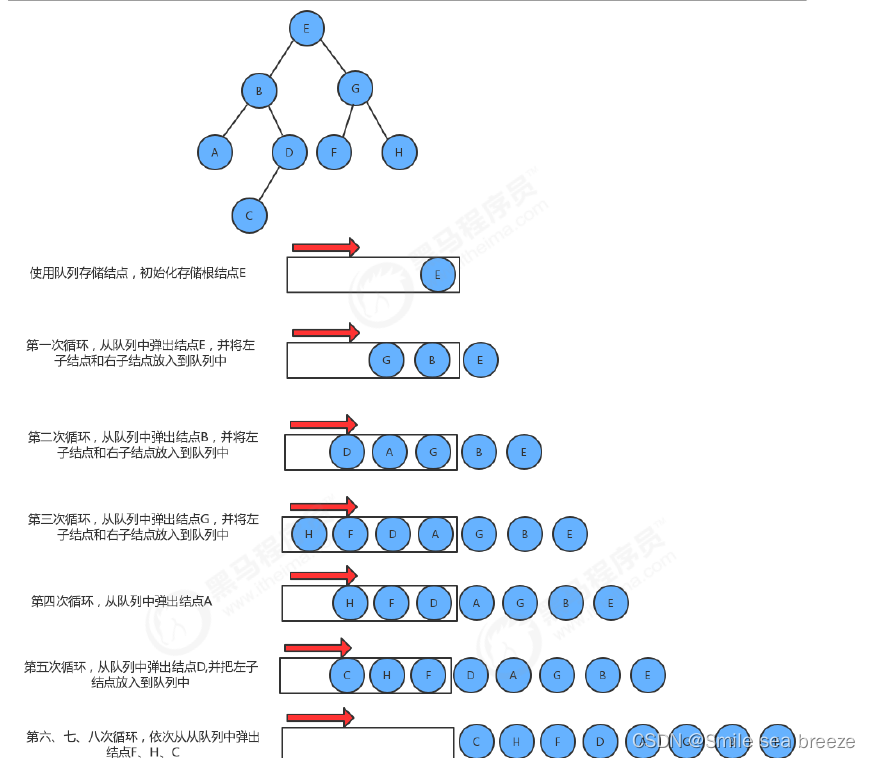
💛前情提要💛
本章节是每日一算法的并查集&带权并查集的相关知识~
接下来我们即将进入一个全新的空间,对代码有一个全新的视角~
以下的内容一定会让你对数据结构与算法有一个颠覆性的认识哦!!!
❗以下内容以C++/java的方式实现,对于数据结构与算法来说最重要的是思想哦❗
以下内容干货满满,跟上步伐吧~
作者介绍:
🎓 作者: 热爱编程不起眼的小人物🐐
🔎作者的Gitee:代码仓库
📌系列文章&专栏推荐: 《刷题特辑》、 《C语言学习专栏》、《数据结构_初阶》 、《C++轻松学_深度剖析_由0至1》、《Linux - 感受系统美学》📒我和大家一样都是初次踏入这个美妙的“元”宇宙🌏 希望在输出知识的同时,也能与大家共同进步、无限进步🌟
🌐这里为大家推荐一款很好用的刷题网站呀👉点击跳转
📌导航小助手📌
- 💡本章重点
- 🍞一.并查集
- 🥐Ⅰ.朴素版并查集
- 🥯Ⅱ.总结
- 🍞二.带权并查集
- 🥐Ⅰ.维护size的并查集
- 🥐Ⅱ.维护dist的并查集
- 🥯Ⅲ.总结
- 🍞三.并查集综合模板
- 🍞四.蓝桥杯A组J题
- 🫓总结
💡本章重点
-
并查集的算法理解
-
带权并查集详解
-
并查集的实际应用:蓝桥杯A组J题 -
推导部分和
🍞一.并查集
💡并查集算法:
-
本质:并查集主要维护的是一个集合,主要作用于
元素分组问题,即可以支持我们快速查询两个元素是否在同一个集合内的操作 -
因此,并查集支持在 O ( 1 ) O(1) O(1) 的时间复杂度内执行以下两个操作:
-
合并:将两个不相交的集合合并为一个集合
-
查询:查询两个元素是否在同一集合内
-
-
思想:在逻辑结构上,每个集合都可以想象成用一棵树来表示,而树的根节点的编号就是整个集合的编号,即对于树中(集合内)的每一个节点存储的都是其父节点
❗特别注意:
-
上述所描述的思想是抽象成以
树的逻辑结构所分析的 -
但在实际应用中,为了提高效率,真正使用的其实是
数组形式的物理结构 -
而这也就解释了为什么可以以 O ( 1 ) O(1) O(1) 的时间复杂度去查询了:
-
正是因为数组拥有
随机访问的特性,从而只要在数组中找到节点所对应的位置,并在此位置上存储其父亲节点,不断往上寻找直至寻找至根节点(即整个集合的编号) -
即可知此节点对应的元素从属于哪个集合,从而也就可以判断任两个元素是否在同一个集合中了
-
👉接下来就让我们深入分析并查集是如何实现的吧~
🥐Ⅰ.朴素版并查集
💡朴素版并查集:
-
此版本的并查集是最基础的
-
而其它版本的并查集也正是由此基础上添加并维护额外信息得出的
👉定义并查集&初始化:
存储每个节点的祖宗节点:
int p[N];
假定节点编号是1~n,并在初始化的时候指向自己:
for (int i = 1; i <= n; i ++ ) p[i] = i;
👆特别注意:
-
每个节点存储其父亲节点,我们采用的是
p[x]:表示x的父节点为p[x]的值 -
【前提:假定节点的编号(即数组的下标)为1~n】也就是说,在初始化阶段的时候,每个节点的父亲节点都是自己,简单来说就是在初始化的时候自己是自成一个集合
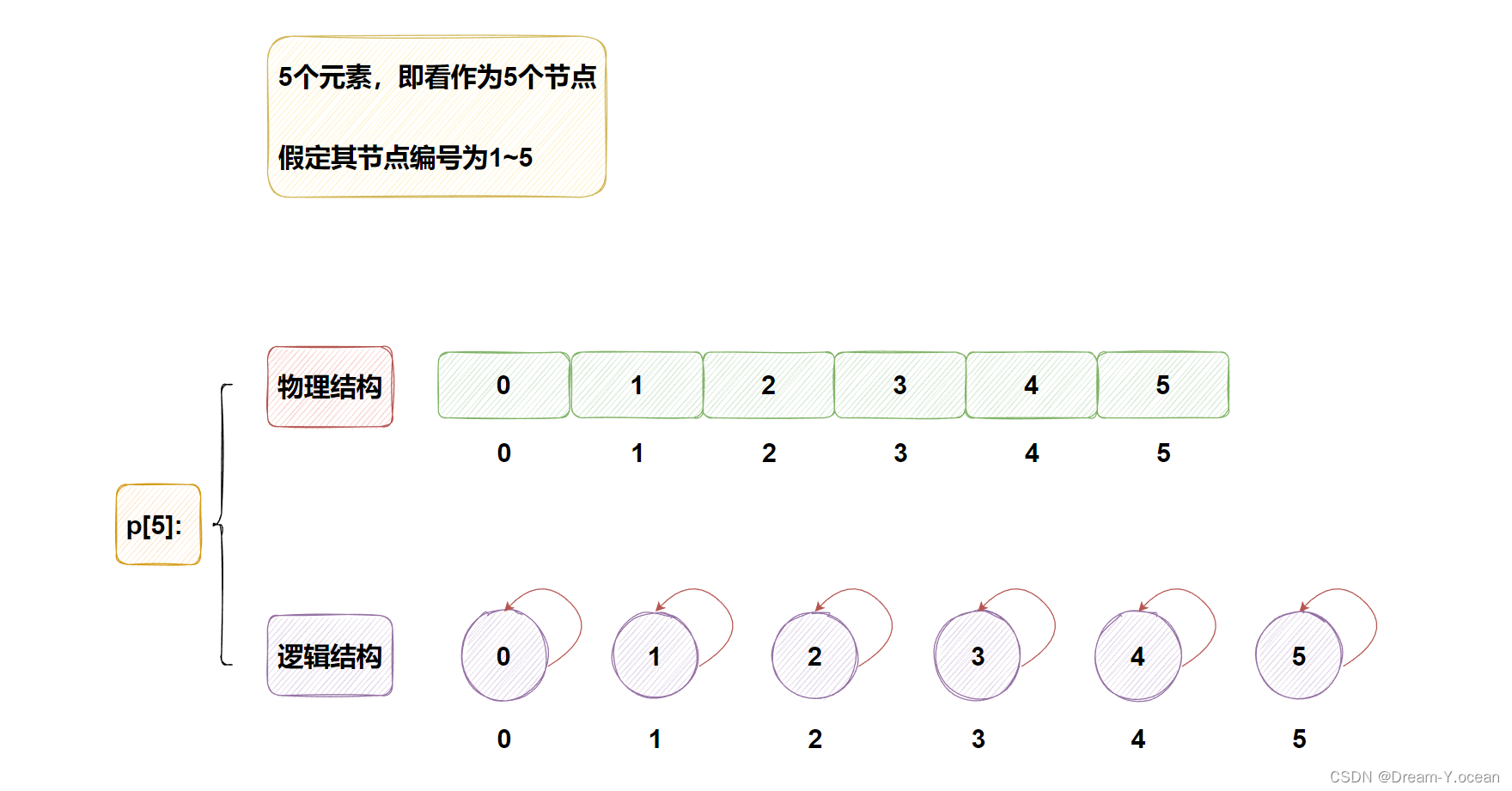
⭐示例:
-
假设目前需要对5个元素进行并查集的操作,而在操作前需要进行初始化
-
初始化后的结构如下:
❓由上述的并查集定义&初始化中,引发了三个问题:
-
🔴如何判断树根,也就是说如何判断已经找到此集合的根节点?
- 答案:只要
if(p[x] == x),即可知此时已经找到此集合的根节点
- 答案:只要
-
🟠如何求x的集合编号,以及如何优化?
-
答案:因为每个节点是存储的是父亲节点,由只要不断迭代,直至根节点为止,那么x元素属于的集合编号就是根节点的编号:
while(p[x] != x) x = p[x]; -
而当前每一次的查找方式的时间复杂度和树的高度次数有关,但我们可以优化为:在找某个节点的根节点的时候,我们可以顺带将此路径上的所有的点都直接指向根节点【即只需要查找一次,这路径上的点都可以一步到位直接指向根节点】
-
也就是说,后续查找某个节点的根节点的时候,无需再由迭代的方式查找根节点了,而是此时的节点直接指向(存储)的就是根节点(集合编号),这个优化方式便叫作:路径压缩优化
-
这样判断两个元素是否在同一集合内就更直接了
-
-
🟡如何合并两个集合?
-
答案:px是x的集合编号,py是y的集合编号,令
p[x] = y;即可 -
即简单来说就是将x的祖宗变为y的祖宗的儿子【将x节点所在的集合的根节点(集合编号)指向y节点所在的集合的根节点(集合编号)】
-
👉解决了上述问题后,我们来具体实现并查集的两个操作吧~
1️⃣优化前的并查集操作:
- 查询操作:
int find(int x)
{
if (x == p[x]) return p[x];
while(p[x] != x) x = p[x];
return p[x];
}
- 合并操作:
bool merge(int x, int y)
{
x = find(x);
y = find(y);
if (x == y) return false;
//将 y节点所在的集合 合并到 x节点的集合上
//【即 将y节点的祖宗 变为 x节点的祖宗】
p[y] = x;
return true;
}
合并操作➕查询操作动图示例:
2️⃣优化后的并查集查询操作:
- 查询操作:
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
👆路径压缩优化细节:
-
优化前的查询操作和优化后的查询操作的不同具体体现在:优化后的查询操作会将查询路径上的节点原本存储的是其父亲节点,而变为直接存储根节点
-
因为
p[N]数组为全局数组,因此函数内对数组的修改会影响到原数组内的值,从而可以借助函数的递归和回溯操作对路径上的节点变为直接指向根节点的值,从而达到优化的效果 -
合并操作➕查询操作动图示例:
👉综上:朴素版并查集整体代码如下
1️⃣定义并查集&初始化:
int p[N];
for (int i = 1; i <= n; i ++ ) p[i] = i;
2️⃣并查集的查询操作:
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
3️⃣并查集的合并操作:
bool merge(int x, int y)
{
x = find(x);
y = find(y);
if (x == y) return false;
p[y] = x;
return true;
}
🥯Ⅱ.总结
⭐综上:
-
以上就是朴素版的并查集的实现啦
-
并查集是被很多人公认的最简洁而优雅的数据结构之一,建议同学们反复阅读掌从而握它呀~
🍞二.带权并查集
💡带权并查集:
- 简单来说:带权并查集就是在朴素并查集的基础上,对朴素并查集中维护集合关系的树中添加边权,并对此维护,以达到维护更多信息的并查集
❓什么是权值:
-
对于带权并查集而言,权值代表着当前节点与父节点的某种关系(即使路径压缩了也是这样),我们便可以通过这两者的关系,将同一棵树下(同一个集合中)两个节点的关系也表示出来
-
而权值在这里一般有两种意思,也就说可以在朴素版的并查集的基础上多维护以下两种信息:
-
1️⃣权值为
size时:表示记录当前并查集集合内的节点个数,也称为维护size的并查集 -
2️⃣权值为
dist时:表示记录当前节点到到祖宗节点距离,也称:维护dist的并查集
-
👉有了以上对带权并查集的了解,接下来就让我们深入了解两种不同的带权并查集吧~
🥐Ⅰ.维护size的并查集
💡维护size的并查集:
-
简单来说:就是在朴素版的并查集的基础上维护多一个信息
size,从而记录当前并查集集合内的节点个数 -
此并查集一般作用于计算
连通块中点的数量的题目
👉代码实现:
1️⃣定义并查集&初始化:
int p[N], _size[N];
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
👆特别注意:
-
p[]存储的是每个点的祖宗节点 -
size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
2️⃣并查集的查询操作:
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
3️⃣并查集的合并操作:
bool merge(int x, int y)
{
x = find(x);
y = find(y);
if (x == y) return false;
_size[x] += _size[y];
p[y] = x;
return true;
}
👆特别注意:
- 因为是合并集合,固然也需要将原来集合内的节点总个数加到新合并的集合中
🌰举个例子:
🥐Ⅱ.维护dist的并查集
💡维护dist的并查集:
-
简单来说:就是在朴素版的并查集的基础上维护多一个信息
dist,从而记录当前节点到根节点之间的距离 -
此并查集一般作用于如:
食物链等题目
👉代码实现:
1️⃣定义并查集&初始化:
int p[N], _dist[N];
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
_dist[i] = 0;
}
👆特别注意:
-
p[]存储的是每个点的祖宗节点 -
d[x]存储的是编号为x的节点到p[x](祖宗节点)的距离
2️⃣并查集的查询操作:
int find(int x)
{
if (p[x] != x)
{
int root = find(p[x]);
_dist[x] += _dist[p[x]];
p[x] = root;
}
return p[x];
}
⭐以上操作的细节:
-
我们需要注意的是,在
路径压缩的过程中,我们需要顺带计算此节点距离祖宗节点的距离,此时我们便需要提前记录每一次递归(即寻找到父亲节点)前的节点的编号 -
即记录下当前所操作的节点编号,这样就能在递归
回溯的时候,对记录下的节点进行距离根节点的距离的更新 -
从而可以达到借助
路径压缩的优化达到不仅仅是对路径节点的优化,也达到了对dist的优化,即一次查询即可更新路径上所有的点到根节点的距离
3️⃣并查集的合并操作:
bool merge(int x, int y)
{
x = find(x);
y = find(y);
if (x == y) return false;
_dist[y] += _dist[x] + 1;
p[y] = x;
return true;
}
❓上述实现中,可能会有如下疑惑:
-
为什么y集合合并到x集合,只需要更新y集合的根节点距离新集合根节点的距离,而不需要将y集合内的所有节点距离新根节点的距离全部更新呢?
-
这是因为:只要后续操作中,需要对原y集合内的某个节点进行
查询操作的时候,查询操作便会对此点所在路径上的所有点全部进行数据的更新,即相当于原y集合内的节点的p[x]和_dist[x]都会更新为指向合并后新的根节点和距离新根节点的距离 -
也就是说,只要合并的时候更新好原根节点距离新根节点的距离,后续只需要一次
查询操作,便可将数据都更新为最新的了
🌰举个例子:
🥯Ⅲ.总结
⭐综上:
-
以上就是带权并查集的全部内容了:
-
若权值体现在集合上,一般开一个
size数组来统计集合的大小 -
若权值体现在边上,可表示当前节点到父节点的距离等意思
-
-
而具体需要使用哪种并查集,维护哪些信息,就需要视具体题意来决定
-
但是,如果遇到需要同时维护
size和dist的情况,我们该怎么办呢?
👉而以下所提及的方法就可以很好解决上述问题啦~
🍞三.并查集综合模板
💡并查集综合模板:
-
在遇到上述所提及的情况的时候,我们再创建现场合并两个并查集就略显麻烦了
-
于是,我们便可以提前将带权并查集将其整合起来,变成一个类(算法模板),对并查集的操作变为类的方法(即
成员函数) -
这样在遇到相应题目的时候,就可以直接调用此类生成一个对象,再调用相应的成员函数去解决啦
-
而且维护成模板的好处是:在做题量丰富的情况下,可以将经常用到的方法(Eg:
判等、求距离……)整合为成员方法,这样就可以有助于我们快速解决题目啦
👉带权并查集算法模板:
//三合一的并查集模板:
//1、朴素版的并查集
//2、维护size【即维护集合中点的数量】
//3、维护集合内的节点到根节点的距离
struct UF {
std::vector<int> p, _dist, _size;
UF(int n)
: p(n) //存储每个点的祖宗节点
, _dist(n, 0) //维护当前到祖宗节点距离的数组
, _size(n, 1) //维护当前的集合中的点的个数的数组(1是因为已经有自己了)
{
//初始化并查集
//假定节点编号为:1~n
for(int i = 1; i <= n; i++) p[i] = i;
}
//路径压缩优化
//顺带维护距离
int find(int x)
{
if (x == p[x]) return p[x];
//先记录祖宗
int root = find(p[x]);
//加上父亲的距离
_dist[x] += _dist[p[x]];
//指向祖宗
return p[x] = root;
}
//判断祖宗节点是否为同一个
//即 判断是否为同一个祖宗
bool same(int x, int y)
{
return find(x) == find(y);
}
//合并并查集
bool merge(int x, int y)
{
x = find(x);
y = find(y);
if (x == y) return false;
//本来d[y](即 祖宗节点 到 祖宗节点的距离)等于0
//现在它指向新祖宗的距离 就是 合并到新集合中 的 新集合中的元素个数
_dist[y] += _size[x];
_size[x] += _size[y];
//将 y节点所在的集合 合并到 x节点的集合上
//【即 将y节点的祖宗 变为 x节点的祖宗】
p[y] = x;
return true;
}
//表示祖宗节点所在集合中的点的数量
int size(int x)
{
return _size[find(x)];
}
//查询两点之间相差几个人,不在一列返回-1
int dist(int x, int y)
{
if (!same(x, y)) return -1;
return abs(p[x] - p[y]) - 1;
}
};
➡️接下来就让我们来道题目实践一下吧~
🍞四.蓝桥杯A组J题
🔍题目传送门:推导部分和
对于一个长度为 N N N 的整数数列 A 1 , A 2 , … A N A_1,A_2,…A_N A1,A2,…AN,小蓝想知道下标 l l l 到 r r r 的部分和 ∑ i = l r A l + A l + 1 + A l + 2 + . . . + A r \sum_{i=l}^r A_l + A_{l+1} + A_{l+2} + ... + A_r ∑i=lrAl+Al+1+Al+2+...+Ar 是多少?
然而,小蓝并不知道数列中每个数的值是多少,他只知道它的 M M M 个部分和的值
其中第 i i i 个部分和是下标 l i l_{i} li 到 r i r_{i} ri 的部分和 ∑ j = l i r i A l i + A l i + 1 + A l i + 2 + . . . + A r i \sum_{j = l_i}^{r_i} A_{l_i} + A_{{l_i}+1} + A_{{l_i}+2} + ... + A_{r_i} ∑j=liriAli+Ali+1+Ali+2+...+Ari ,值是 S i S_i Si
输入格式:
第一行包含 3 个整数 N N N 、 M M M 和 Q Q Q ,分别代表数组长度、已知的部分和数量和询问的部分和数量
接下来 M M M 行, 每行包含 3 个整数 l i l_i li、 r i r_i ri、 S i S_i Si
接下来 Q Q Q 行,每行包括 2 个整数 l l l 和 r r r,代表一个小蓝想知道的部分和
输出格式:
对于每个询问, 输出一行包含一个整数表示答案
如果答案无法确定, 输出 UNKNOWN
数据范围:
1 ≤ N , M , Q ≤ 1 0 5 1 \leq N, M, Q \leq 10^{5} 1≤N,M,Q≤105
− 1 0 12 ≤ S i ≤ 1 0 12 -10^{12} \leq S_{i} \leq 10^{12} −1012≤Si≤1012
1 ≤ l i ≤ r i ≤ N 1 \leq l_{i} \leq r_{i} \leq N 1≤li≤ri≤N
1 ≤ l ≤ r ≤ N 1≤l≤r≤N 1≤l≤r≤N
样例输入:
5 3 3
1 5 15
4 5 9
2 3 5
1 5
1 3
1 2
样例输出:
15
6
UNKNOWN
💡解题关键:
-
其实题目的本质:就是给了一个前缀和数组的下标以及这段区间的区间和,让我们去判断能否利用已知的区间和区间,判断能否计算出询问区间的区间和,若能就输出答案
-
不了解
前缀和相关算法知识的同学可>点击<跳转食用呀
➡️拆分思路:
-
1️⃣针对求前缀和数组中的某一段区间 [ l 已 知 , r 已 知 ] [l_{已知},r_{已知}] [l已知,r已知] 的和,所使用的计算公式是 s [ r 已 知 ] − s [ l 已 知 − 1 ] s[r_{已知}] - s[l_{已知} - 1] s[r已知]−s[l已知−1]
-
2️⃣也就是说,只要询问时给出区间范围 [ l 问 , r 问 ] [l_问,r_问] [l问,r问] 满足已知的区间和范围 l 已 知 − 1 = l 未 知 − 1 l_{已知} - 1 = l_{未知} - 1 l已知−1=l未知−1 和 r 已 知 = r 未 知 r_{已知} = r_{未知} r已知=r未知 的时候,就一定满足此次询问的区间的区间和是一定可以被计算出来的
-
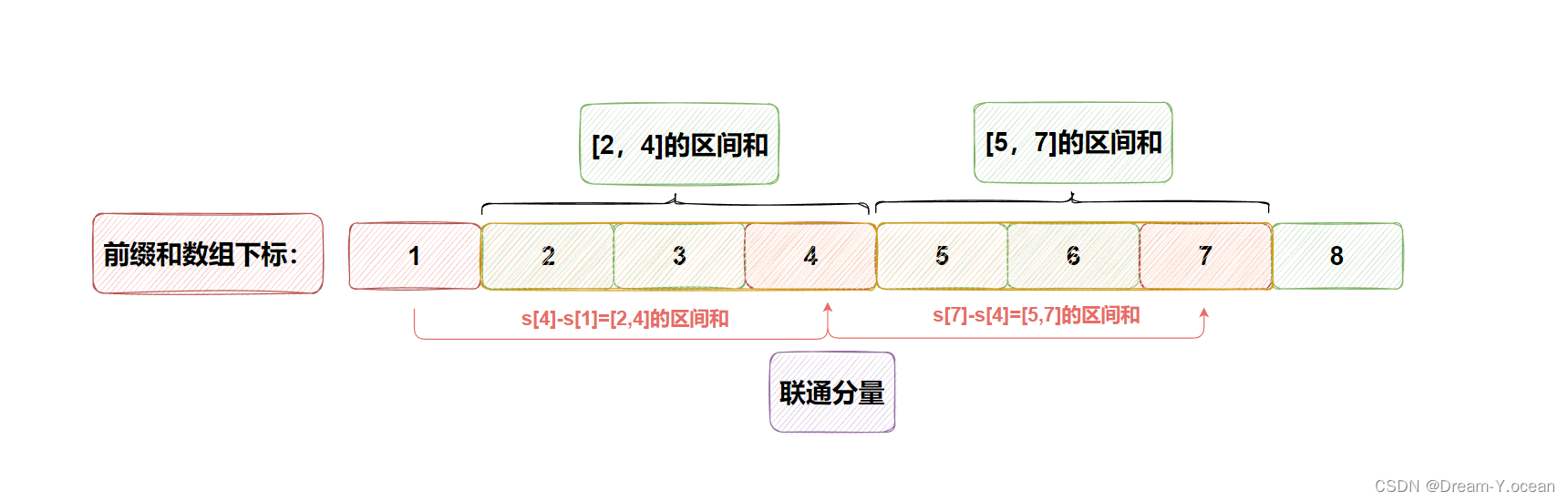
3️⃣而且区间和的范围是具有
合并性(连通性)的,Eg:假设存在前缀和数组,且数组下标为: [1 2 3 4 5 6 7] ,已知区间和的(下标)范围为: [2,4]、[5,7]-
通过上述可知:⌈ s[4] - s[1] = [2,4] 的区间和 ⌋ 、⌈ s[7] - s[4] = [5,7] 的区间和 ⌋
-
也就说明,此时我们可以通过上述两个式子合并为:⌈ s[7] - s[1] ⌋,从而得出: ⌈ [2,7] 的区间和 ⌋
-
👆综上:
-
有了上述的两个性质,我们便可知如果需要维护
连通分量的话,就需要用到并查集的数据结构 -
即只要维护好如上述例子中的
1、4、7这样的连通分量,后续只需要判断 ⌈ l 未 知 − 1 l_{未知}-1 l未知−1⌋ 与 ⌈ r 未 知 r_{未知} r未知⌋ 是否同属于一个集合中即可 -
因为只要将连通分量放在一个并查集中管理,而且并查集的根节点为最大的联通的分量,这样就能保证只要在并查集内找到任意两个连通分量同属于一个集合的话,都是可以依靠这两个连通分量计算出区间和的
❗特别注意:
-
题目不仅仅要我们判断是否能求解出,更要输出给出的范围的区间和
-
此时,我们采取
朴素版并查集就只能满足一个要求,做不到记录连通分量之间的区间和的需求,于是我们便可以依此增加边权:维护当前节点至根节点的距离 -
而这里的距离指的是:当前节点与根节点范围间的区间和【即当前连通变量与最大连通变量范围之间的区间和】
-
所以,我们用的是:带权并查集(
维护dist的并查集),计算求解区间 [ l , r ] [ l , r ] [l,r] 时,只需要用 d i s t [ r ] − d i s t [ l − 1 ] dist [ r ] − dist [ l − 1 ] dist[r]−dist[l−1] 即可【但这样计算出来的是负数,因为我们规定了一个集合内根节点的编号为最大连通分量(即右范围),所以 d i s t [ l − 1 ] − d i s t [ r ] dist [ l - 1 ] − dist [ r ] dist[l−1]−dist[r] 才是正数】
⭐这里,就可以很好体现并查集模板的作用了,我们只需要直接套模板做题就可以很快解决了【C++、Java同理】
👉C++代码实现:
#include <iostream>
#include <vector>
using namespace std;
struct UF {
std::vector<long long> p, _dist, _size;
UF(int n)
: p(n) //存储每个点的祖宗节点
, _dist(n, 0) //维护当前到祖宗节点距离的数组
, _size(n, 1) //维护当前的集合中的点的个数的数组(1是因为已经有自己了)
{
for(int i = 1; i <= n; i++) p[i] = i;
}
int find(int x)
{
if (x == p[x]) return p[x];
int root = find(p[x]);
_dist[x] += _dist[p[x]];
return p[x] = root;
}
bool same(int x, int y)
{
return find(x) == find(y);
}
//合并并查集
bool merge(int x, int y, long long w)
{
int u = find(x);
int v = find(y);
if (u == v) return false;
_dist[v] = w - _dist[y] + _dist[x];
_size[u] += _size[v];
p[v] = u;
return true;
}
int size(int x)
{
return _size[find(x)];
}
int dist(int x, int y)
{
if (!same(x, y)) return -1;
return abs(p[x] - p[y]) - 1;
}
};
int n,m,q;
long long s;
int main()
{
cin >> n >> m >> q;
UF uf(n + 10);
for(int i = 0; i < m; i++)
{
int l = 0, r = 0;
cin >> l >> r >> s;
uf.merge(r, l - 1, s);
}
for(int i = 0; i < q; i++)
{
int l = 0, r = 0;
cin >> l >> r;
if(uf.same(l-1, r) == false)
{
cout << "UNKNOWN" << endl;
}
else
{
cout << uf._dist[l - 1] - uf._dist[r] << endl;
}
}
return 0;
}
👉Java代码实现:
import java.util.Scanner;
public class PartialSum {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int M = in.nextInt();
int Q = in.nextInt();
int[] father = new int[N + 1];// 每个节点的父节点
for (int i = 0; i <= N; i++) {
father[i] = i;
}
// value[i]表示i到其根节点的路径长度
// 本题中,左区间从0开始,计算部分和时不包括左端点的值。
// 原因:求1到2位置上的部分和时,若并查集结构为(1->2),此时1到2之间就只能
// 有一个权值,即只能知道1或者2位置上的值,所以并查集结构应改为(0->1->2),
// 即(0->1)的边权值表示1位置的值,(1->2)的边权值表示2位置的值,此时求1到2位置
// 上数字和时,即(0->1->2)路径的权值和
long[] value = new long[N + 1];
while (M > 0) {
int l = in.nextInt();
int r = in.nextInt();
long s = in.nextLong();
l--;
// 找根节点,并压缩路径
int l_Father = findFather(l, father, value);
int r_Father = findFather(r, father, value);
if (l_Father != r_Father) {
// 合并l和r的集合,并更新权值
// 合并规则,将小根节点集合指向大根节点集合
int small = l_Father > r_Father ? r_Father : l_Father;
int big = small == r_Father ? l_Father : r_Father;
father[small] = big;
value[small] = Math.abs(-value[l] + value[r] + s);
}
M--;
}
while (Q > 0) {
int l = in.nextInt();
int r = in.nextInt();
l--;
int l_Father = findFather(l, father, value);
int r_Father = findFather(r, father, value);
// 同一集合,就能计算出其结果
if (l_Father == r_Father) {
System.out.println(value[l] - value[r]);
} else {
System.out.println("UNKNOWN");
}
Q--;
}
}
// 查找;路径压缩
static int findFather(int x, int[] father, long[] value) {
if (x != father[x]) {
int temp = father[x];
father[x] = findFather(father[x], father, value);// 找根节点
value[x] += value[temp];// 压缩路径
}
return father[x];
}
}
🔔这里需要转换一下:
-
如上模板中更新距离的时候需要做出一点变化:
-
这里的
距离更新是指:更新 节点合并前所在的集合的根节点 到 合并到新的集合后的新的根节点 之间的路程 -
所以上述距离的计算式子
_dist[v] = w - _dist[y] + _dist[x]表达的意思是:-
1️⃣
_dist[v]:表示的是 合并操作前的集合的根节点 到 合并后所在集合的根节点的路程【也就是在合并之前,根节点自己的距离都为0,因为是指向自己的,但现在执行的是合并操作,所以需要更新此根节点到新集合的根节点的距离】 -
2️⃣
w - _dist[y]:表示的是 原本要去合并的节点 到 新集合中的根节点的路程 ➖ 原本要去合并的节点 到 自己集合中的根节点的路程,也就是说:计算的其实是 自己集合中的根节点 到 要合并到的新集合中的根节点的路程 -
3️⃣
_dist[x]:表示的是 合并到新集合后的合并点到此根节点的路程 ,而之所以要加上它,是因为我们操作的时候不一定是直接合并到新集合中的根节点,有可能是新集合中的某个点,也就是说合并点不一定是新集合的根节点-
所以,如果是合并到新集合中的某个点的情况的时候,还需要加上此点到根节点之间的路程,才真正是 节点合并前所在的集合的根节点 到 合并到新的集合后的新的根节点 之间的路程
-
而如果合并点为根节点的话【即直接合并到新集合中的根节点】,
_dist[x]其实为0,因为根节点距离自己的距离为0,所以即使加上也不会影响最终结果
-
-
🫓总结
综上,我们基本了解了算法基础中的 “并查集&带权并查集” 🍭 的知识啦~~
恭喜你的内功又双叒叕得到了提高!!!
感谢你们的阅读😆
后续还会继续更新💓,欢迎持续关注📌哟~
💫如果有错误❌,欢迎指正呀💫
✨如果觉得收获满满,可以点点赞👍支持一下哟~✨