二叉树-二叉树的基础遍历（3）

news2024/12/24 3:10:10

二叉树的遍历的三种方式

1.前序遍历；
先访问根结点，然后再访问左子树，最后访问右子树
2.中序遍历；
先访问左子树，中间访问根节点，最后访问右子树
3.后序遍历；
先访问左子树，再访问右子树，最后访问根节点
如果我们分别对下面的树使用三种遍历方式进行遍历，得到的结果如下：
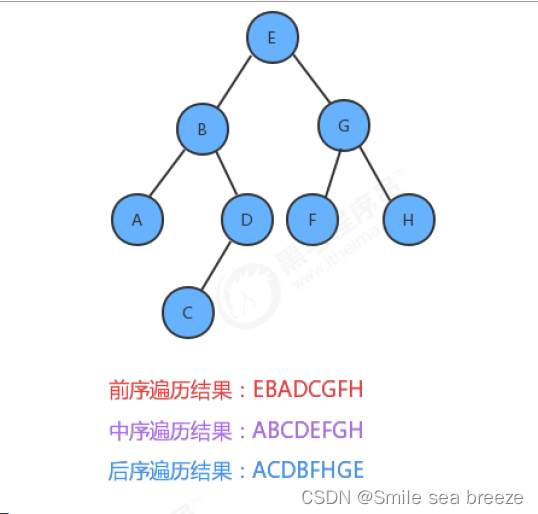
在这里插入图片描述

前序遍历

前序遍历的API：
public Queue preErgodic()：使用前序遍历，获取整个树中的所有键
private void preErgodic(Node x,Queue keys)：使用前序遍历，把指定树x中的所有键放入到keys队列中
实现步骤：
1.把当前结点的key放入到队列中;
2.找到当前结点的左子树，如果不为空，递归遍历左子树
3.找到当前结点的右子树，如果不为空，递归遍历右子树

代码实现：

//使用前序遍历，获取整个树中的所有键
public Queue<Key> preErgodic(){
	Queue<Key> keys = new Queue<>();
	preErgodic(root,keys);
	return keys;
}
//使用前序遍历，把指定树x中的所有键放入到keys队列中
private void preErgodic(Node x,Queue<Key> keys){
	if (x==null){
	return;
}
	//1.把当前结点的key放入到队列中;
	keys.enqueue(x.key);
	//2.找到当前结点的左子树，如果不为空，递归遍历左子树
	if (x.left!=null){
		preErgodic(x.left,keys);
	}
	//3.找到当前结点的右子树，如果不为空，递归遍历右子树
	if (x.right!=null){
		preErgodic(x.right,keys);
	}
}
	//测试代码
	public class Test {
		public static void main(String[] args) throws Exception {
		BinaryTree<String, String> bt = new BinaryTree<>();
			bt.put("E", "5");
			bt.put("B", "2");
			bt.put("G", "7");
			bt.put("A", "1");
			bt.put("D", "4");
			bt.put("F", "6");
			bt.put("H", "8");
			bt.put("C", "3");
		Queue<String> queue = bt.preErgodic();
		for (String key : queue) {
			System.out.println(key+"="+bt.get(key));
		}
	}
}

运行结果：

5=E
2=B
1=A
4=D
3=C
7=G
6=F
8=H

中序遍历

前序遍历的API：
public Queue midErgodic()：使用中序遍历，获取整个树中的所有键
private void midErgodic(Node x,Queue keys)：使用中序遍历，把指定树x中的所有键放入到keys队列中
实现步骤：
1.找到当前结点的左子树，如果不为空，递归遍历左子树
2.把当前结点的key放入到队列中;
3.找到当前结点的右子树，如果不为空，递归遍历右子树

代码实现：

//使用中序遍历，获取整个树中的所有键
	public Queue<Key> midErgodic(){
		Queue<Key> keys = new Queue<>();
		midErgodic(root,keys);
		return keys;
	}
	//使用中序遍历，把指定树x中的所有键放入到keys队列中
	private void midErgodic(Node x,Queue<Key> keys){
	if (x==null){
		return;
	}
	//1.找到当前结点的左子树，如果不为空，递归遍历左子树
	if (x.left!=null){
		midErgodic(x.left,keys);
	}
	//2.把当前结点的key放入到队列中;
	keys.enqueue(x.key);
	//3.找到当前结点的右子树，如果不为空，递归遍历右子树
	if (x.right!=null){
		midErgodic(x.right,keys);
	}
}
//测试代码
public class Test {
	public static void main(String[] args) throws Exception {
	BinaryTree<String, String> bt = new BinaryTree<>();
	bt.put("E", "5");
	bt.put("B", "2");
	bt.put("G", "7");
	bt.put("A", "1");
	bt.put("D", "4");
	bt.put("F", "6");
	bt.put("H", "8");
	bt.put("C", "3");
	Queue<String> queue = bt.midErgodic();
	for (String key : queue) {
		System.out.println(key+"="+bt.get(key));
	}
	}
}

运行结果：

1=A
2=B
3=C
4=D
5=E
6=F
7=G
8=H

后序遍历

后序遍历的API：
public Queue afterErgodic()：使用后序遍历，获取整个树中的所有键
private void afterErgodic(Node x,Queue keys)：使用后序遍历，把指定树x中的所有键放入到keys队列中
实现步骤：
1.找到当前结点的左子树，如果不为空，递归遍历左子树
2.找到当前结点的右子树，如果不为空，递归遍历右子树
3.把当前结点的key放入到队列中;

代码实现：

//使用后序遍历，获取整个树中的所有键
public Queue<Key> afterErgodic(){
	Queue<Key> keys = new Queue<>();
	afterErgodic(root,keys);
	return keys;
}
//使用后序遍历，把指定树x中的所有键放入到keys队列中
private void afterErgodic(Node x,Queue<Key> keys){
	if (x==null){
	return;
}
//1.找到当前结点的左子树，如果不为空，递归遍历左子树
if (x.left!=null){
	afterErgodic(x.left,keys);
}
//2.找到当前结点的右子树，如果不为空，递归遍历右子树
if (x.right!=null){
	afterErgodic(x.right,keys);
}
//3.把当前结点的key放入到队列中;
keys.enqueue(x.key);
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
	BinaryTree<String, String> bt = new BinaryTree<>();
	bt.put("E", "5");
	bt.put("B", "2");
	bt.put("G", "7");
	bt.put("A", "1");
	bt.put("D", "4");
	bt.put("F", "6");
	bt.put("H", "8");
	bt.put("C", "3");
	Queue<String> queue = bt.afterErgodic();
	for (String key : queue) {
		System.out.println(key+"="+bt.get(key));
	}
}
}

运行结果：

1=A
3=C
4=D
2=B
6=F
8=H
7=G
5=E

二叉树的层序遍历

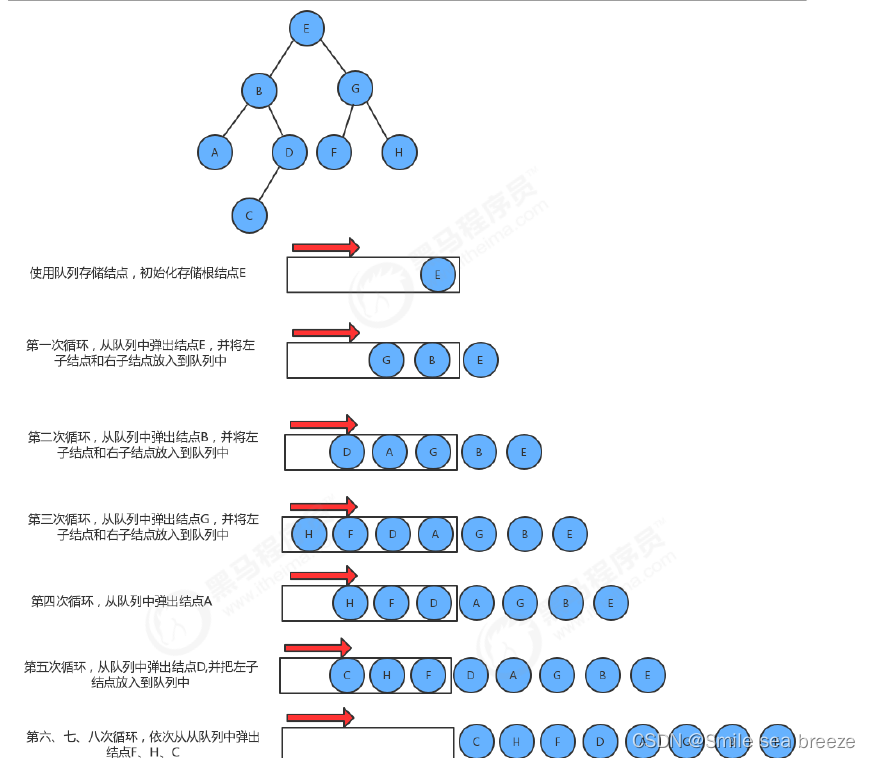
所谓的层序遍历，就是从根节点（第一层）开始，依次向下，获取每一层所有结点的值，有二叉树如下：
那么层序遍历的结果是：EBGADFHC
层序遍历的API：
public Queue layerErgodic()：使用层序遍历，获取整个树中的所有键
实现步骤：
1.创建队列，存储每一层的结点；
2.使用循环从队列中弹出一个结点：
2.1获取当前结点的key；
2.2如果当前结点的左子结点不为空，则把左子结点放入到队列中
2.3如果当前结点的右子结点不为空，则把右子结点放入到队列中
在这里插入图片描述
代码：

//使用层序遍历得到树中所有的键
public Queue<Key> layerErgodic(){
	Queue<Key> keys = new Queue<>();
	Queue<Node> nodes = new Queue<>();
	nodes.enqueue(root);
	while(!nodes.isEmpty()){
		Node x = nodes.dequeue();
		keys.enqueue(x.key);
		if (x.left!=null){
		nodes.enqueue(x.left);
	}
	if (x.right!=null){
		nodes.enqueue(x.right);
	}
	}
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
	BinaryTree<String, String> bt = new BinaryTree<>();
	bt.put("E", "5");
	bt.put("B", "2");
	bt.put("G", "7");
	bt.put("A", "1");
	bt.put("D", "4");
	bt.put("F", "6");
	bt.put("H", "8");
	bt.put("C", "3");
	Queue<String> queue = bt.layerErgodic();
	for (String key : queue) {
	System.out.println(key+"="+bt.get(key));
	}
}
}

结果：

5=E
2=B
7=G
1=A
4=D
6=F
8=H
3=C

参考：黑马程序员Java数据结构与java算法全套教程

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/87178.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

PicoRV32 笔记 05

PicoRV32 笔记 05

接口信号 PicoRV32 提供一个本地存储器接口&#xff0c;Native Memory Interface。 本地存储器接口采用 valid-ready握手信号。这种机制在axi总线中使用相同&#xff0c;能够实现流控&#xff0c; 和axi总线不同点&#xff0c;PicoRV32本地接口使用一组valid-ready信号&…
阅读更多...
什么是SWDM4和100G QSFP28 SWDM4光模块？

什么是SWDM4和100G QSFP28 SWDM4光模块？

随着OM5多模光纤(MMF)的推广和40G或100G数据中心传输网络的大规模部署&#xff0c;SWDM技术逐渐进入人们的视野并开始得到应用。那么&#xff0c;什么是SWDM4呢&#xff1f;什么是100G SWDM4光模块&#xff1f;它们的优势是什么&#xff1f;跟着易天光通信ETU-LINK看下面的文字…
阅读更多...
十、原型、原型链、闭包和立即执行函数、插件开发初始

十、原型、原型链、闭包和立即执行函数、插件开发初始

十、原型、原型链、闭包和立即执行函数、插件开发初始 原型 什么是原型&#xff08;prototype&#xff09;&#xff1f; 无论何时&#xff0c;只要创建一个函数&#xff0c;就会按照特定的规则为这个函数创建一个prototype属性&#xff0c;指向原型对象。 function Car(){}…
阅读更多...
Vue入门与指令

Vue入门与指令

Vue入门 1.1、MVVM编程思想 MVVM&#xff1a;页面输入改变数据&#xff0c;数据改变影响页面数据展示与渲染。 M&#xff08;model&#xff09;&#xff1a;普通的javascript数据对象。 V&#xff08;view&#xff09;&#xff1a;前端展示页面。 VM&#xff08;ViewModel&…
阅读更多...
Jmeter初了解-接口并发测试

Jmeter初了解-接口并发测试

Jmeter初了解-接口并发测试 介绍 我们在开发的时候&#xff0c;经常会需要进行接口压力测试&#xff0c;确定接口运行的稳定情况 这里我们就使用java开发的测试工具Jmeter来进行测试。 Jmeter 官网地址 Apache JMeter™应用程序是开源软件&#xff0c;是一个 100% 纯 Jav…
阅读更多...
Pytorch安装详细过程及遇到的问题解决

Pytorch安装详细过程及遇到的问题解决

一、Aanconda的安装 可以参考笔者的这篇博客&#xff1a;Anaconda安装详细教程 二、准备工作 1、查看本机的python的版本(本机python解释器版本为3.8.5) 2、单击启动Anaconda Prompt创建新虚拟环境 3、在Anaconda Prompt依次执行以下命令&#xff0c;创建名字为pytorch的虚拟…
阅读更多...
nn.Embedding使用

nn.Embedding使用

nn.Embedding是一种词嵌入的方式&#xff0c;跟one-hot相似但又不同&#xff0c;会生成低维稠密向量&#xff0c;但是初始是随机化的&#xff0c;需要根据模型训练时进行调节&#xff0c;若使用预训练词向量模型会比较好。 1. one-hot one-hot是给定每个单词一个索引&#xf…
阅读更多...
概论_第4章__方差D(X)的定义和性质

概论_第4章__方差D(X)的定义和性质

一 定义 通常以此公式来计算&#xff1a; 就是说&#xff1a; 方差 X的平方再求期望 —— X的期望的平方 即 括号里面的平方的期望减去期望的平方&#xff0c; 怎样求期望点击&#xff1a;概论_第4章__期望的定义和性质 注意&#xff1a; 方差不可能为负数。 2. …
阅读更多...
如何快速拥有自己的虚拟形象？

如何快速拥有自己的虚拟形象？

元宇宙&#xff08;Metaverse&#xff09;&#xff0c;是人类运用数字技术构建的&#xff0c;由现实世界映射或超越现实世界&#xff0c;可与现实世界交互的虚拟世界&#xff0c;具备新型社会体系的数字生活空间。 可见元宇宙第一步是创建专属虚拟形象&#xff0c;但创建3D虚拟…
阅读更多...
Android入门第45天-手工发送一个BroadCast

Android入门第45天-手工发送一个BroadCast

简介 上一篇我们讲了简单的动态BroadCast&#xff0c;今天我们通过手工来发送一条BroadCast进一步来了解BroadCast。 在上一篇里我们使用BroadCast监听网络状态&#xff0c;今天我们要完成的是自己发一条自自己的消息来触发BroadCast Receiver。 设计 为了让Receiver收听到…
阅读更多...
蓝牙耳机无延迟哪款好?适合打游戏的无线蓝牙耳机

蓝牙耳机无延迟哪款好?适合打游戏的无线蓝牙耳机

手机可以说是人手必备&#xff0c;随声得还有蓝牙耳机&#xff0c;随着3.5耳机孔得消失&#xff0c;蓝牙耳机可以说是现在得主流&#xff0c;无论哪个年龄段都可以佩戴蓝牙耳机&#xff0c;日常听歌、追剧&#xff0c;和朋友玩游戏佩戴蓝牙耳机&#xff0c;已经成为一种生活方式…
阅读更多...
mybatis06:MyBatis的多表操作

mybatis06:MyBatis的多表操作

目录 1.一对一关系 2.一对多查询 3.多对多查询 4例题演示 ​5.知识小结 1.一对一关系 2.一对多查询 3.多对多查询 4例题演示 前置准备 对应的依赖 <dependencies><!-- mysql驱动 --><dependency><groupId>mysql</groupId><artifactId&…
阅读更多...
外汇交易：流行图表指标盘点

外汇交易：流行图表指标盘点

您所学到的关于交易的一切都像一种工具&#xff0c;已被添加到外汇交易者的工具箱中。当您在正确的时间使用正确的工具时&#xff0c;您的图表指标工具将为您提供更好的机会做出正确的交易决策。 布林带 布林带用来衡量市场的波动性。它们的作用类似于迷你支撑位和阻力位。 布…
阅读更多...
MES系统为何与工厂数字化转型联系紧密

MES系统为何与工厂数字化转型联系紧密

随着数字化技术的发展&#xff0c;MES系统的定义也是在不断的变化。但是&#xff0c;计划调度、质量管理、生产执行以及数据采集&#xff0c;一直都是MES的核心功能。 工厂数字化改造&#xff0c;对于制造业来说并不是一场革命。很多工厂在十年前就实现了车间设备的联网&#…
阅读更多...
EXCEL基础：数据有效性设置与从身份证号码提取出生日期、性别操作

EXCEL基础：数据有效性设置与从身份证号码提取出生日期、性别操作

如下所示&#xff0c;为某公司的人员信息表&#xff0c;以下操作均是基于该表格&#xff0c;声明&#xff1a;该表格来自网络&#xff01; 下面进行【数据有效性】的设置&#xff1a; 先选中区域&#xff0c;弹出【数据有效性】对话框&#xff0c;在【设置】里的【允许】里输入…
阅读更多...
win11设置java环境变量

win11设置java环境变量

python环境变量比java简单很多&#xff0c;而java比较麻烦&#xff0c;下面这些步骤应该是一步不能少&#xff0c;必须新建两个而且移动到最上面 一、找到设置环境变量 只要是windows系统&#xff0c;他就长这样&#xff0c;需要找到这个页面 很多之前的文章都会说&#xff1…
阅读更多...
[附源码]Node.js计算机毕业设计电影院订票系统Express

[附源码]Node.js计算机毕业设计电影院订票系统Express

项目运行 环境配置&#xff1a; Node.js最新版 Vscode Mysql5.7 HBuilderXNavicat11Vue。 项目技术&#xff1a; Express框架 Node.js Vue 等等组成&#xff0c;B/S模式 Vscode管理前后端分离等等。 环境需要 1.运行环境&#xff1a;最好是Nodejs最新版&#xff0c;我…
阅读更多...
六、作用域，作用域链，预编译，闭包基础

六、作用域，作用域链，预编译，闭包基础

六、作用域&#xff0c;作用域链&#xff0c;预编译&#xff0c;闭包基础 使用AO,GO说明作用域和作用域链 AO与函数有关&#xff0c;函数能创造出独立的空间&#xff0c;但是这句话不太对&#xff0c;接下来就是解释&#xff1a; 对象 每个对象都有属性和方法&#xff1a; …
阅读更多...
MobileNetV2原理说明及实践落地

MobileNetV2原理说明及实践落地

本文参考&#xff1a; 轻量级网络——MobileNetV2_Clichong的博客-CSDN博客_mobilenetv2 1、MobileNetV2介绍 MobileNetV1主要是提出了可分离卷积的概念&#xff0c;大大减少了模型的参数个数&#xff0c;从而缩小了计算量。但是在CenterNet算法中作为BackBone效果并不佳&…
阅读更多...
【MATLAB教程案例59】使用matlab实现基于LSTM网络的数据分类预测功能与仿真分析

【MATLAB教程案例59】使用matlab实现基于LSTM网络的数据分类预测功能与仿真分析

欢迎订阅《FPGA学习入门100例教程》、《MATLAB学习入门100例教程》 目录 1.软件版本 2.LSTM网络理论概述
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023