本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
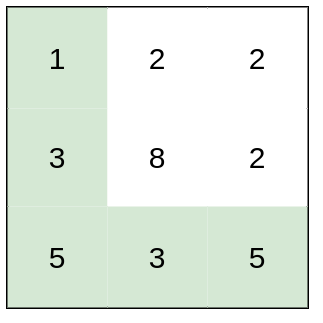
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
示例 2:
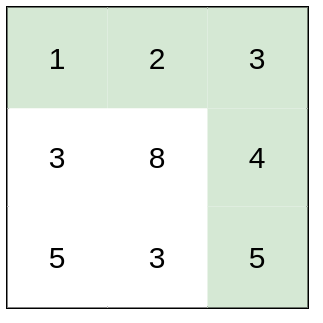
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
示例 3:
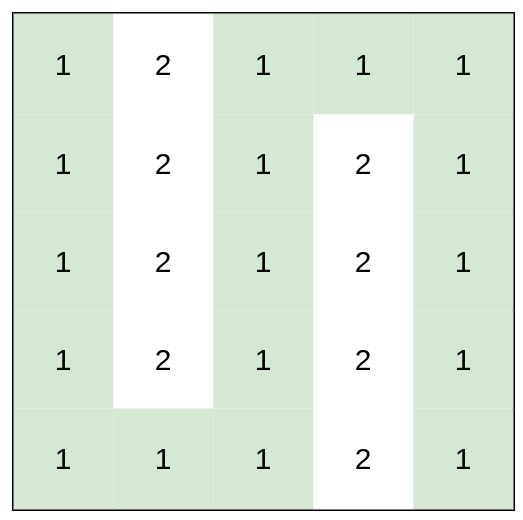
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 10^6
同类题目:
- LeetCode 2812. Find the Safest Path in a Grid
- LeetCode 778. Swim in Rising Water
- LeetCode 1631. 最小体力消耗路径
这几道题,虽然物理问题不同,但是背后的数学模型几乎完全相同,唯一的区别在于:
- 第 1631 题将相邻格子的高度差作为边的权重,是找最小化的 相邻格子最大绝对高度差。
- 第 778 题将相邻两格子间高度的最大值作为边的权重,是找最小化的 最大高度
- 第 2812 题将当前方格到最近小偷的距离作为边的权重,是找最大化的 最小距离
无向图 G G G 中 x x x 到 y y y 的最小瓶颈路是这样的一类简单路径,满足这条路径上的最大边权在所有 x x x 到 y y y 的简单路径中是最小的。
根据最小生成树定义, x x x 到 y y y 的最小瓶颈路上的最大边权等于最小生成树上 x x x 到 y y y 路径上的最大边权。虽然最小生成树不唯一,但是每种最小生成树 x x x 到 y y y 路径的最大边权相同且为最小值。也就是说,每种最小生成树上的 x x x 到 y y y 的路径均为最小瓶颈路。
无向图 G G G 中 x x x 到 y y y 的最大瓶颈路是这样的一类简单路径,满足这条路径上的最小边权在所有 x x x 到 y y y 的简单路径中是最大的。
根据最小生成树定义, x x x 到 y y y 的最大瓶颈路上的最小边权等于最大生成树上 x x x 到 y y y 路径上的最小边权。虽然最大生成树不唯一,但是每种最大生成树 x x x 到 y y y 路径的最小边权相同且为最大值。也就是说,每种最大生成树上的 x x x 到 y y y 的路径均为最大瓶颈路。
我们不必实际求出整个最小/大生成树,只需要求出最小/大生成树上 x x x 到 y y y 路径上的最大/小边权。
在看清楚物理问题背后的数学模型后,这几道题都会迎刃而解。
解法1 二分+BFS/DFS
这种做法是LeetCode 2812. Find the Safest Path in a Grid的完全简化版、在2812中需要先进行一次多源BFS、再来二分答案,也用在LeetCode 1631. 最小体力消耗路径中。
根据题目中的描述,给定了 h e i g h t s [ i ] [ j ] heights[i][j] heights[i][j] 的范围是 [ 1 , 1 0 6 ] [1, 10^6 ] [1,106] ,所以答案(绝对高度差)必然落在范围 [ 0 , 1 0 6 ] [0, 10^6] [0,106] :
- 如果允许消耗的体力值 h h h 越低,网格上可以越过的部分就越少,存在从左上角到右下角的一条路径的可能性越小
- 如果允许消耗的体力值 h h h 越高,网格上可以游泳的部分就越多,存在从左上角到右下角的一条路径的可能性越大。
这是本问题具有的 单调性 。因此可以使用二分查找定位到最小体力消耗值。
假设最优解为 l l l 的话(恰好能到达右下角的体力消耗),那么小于 l l l 的体力消耗无法到达右下角,大于 l l l 的体力消耗能到达右下角,因此在以最优解 l l l 为分割点的数轴上具有二段性,可以通过「二分」找到分割点 l l l 。
注意:「二分」的本质是两段性,并非单调性。只要一段满足某个性质,另外一段不满足某个性质,就可以用「二分」。其中 33. 搜索旋转排序数组 是一个很好的说明例子。
具体来说:在区间 [ 0 , 1 e 6 ] [0,1e6] [0,1e6] 里猜一个整数,针对这个整数从起点(左上角)开始做一次DFS或BFS:
- 当小于等于该数值时,如果存在一条从左上角到右下角的路径,说明答案可能是这个数值,也可能更小;
- 当小于等于该数值时,如果不存在一条从左上角到右下角的路径,说明答案一定比这个数值更大。
- 按照这种方式不断缩小搜索的区间,最终找到最小体力消耗。
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
int n = heights.size(), m = heights[0].size();
typedef pair<int, int> pii;
int d[4][2] = {-1, 0, 1, 0, 0, -1, 0, 1};
auto check = [&](int lim) {
bool vis[n][m]; memset(vis, false, sizeof(vis));
queue<pii> q;
q.push(pii(0, 0)); vis[0][0] = true;
while (!q.empty()) {
pii p = q.front(); q.pop();
int i = p.first, j = p.second;
if (i == n - 1 && j == m - 1) return true;
for (int k = 0; k < 4; ++k) {
int x = i + d[k][0], y = j + d[k][1];
if (x < 0 || x >= n || y < 0 || y >= m ||
abs(heights[x][y] - heights[i][j]) > lim || vis[x][y])
continue;
q.push(pii(x, y));
vis[x][y] = true;
}
}
return vis[n - 1][m - 1];
};
int l = 1, r = 1e6 + 1;
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
};
复杂度分析:
- 时间复杂度: O ( M N log C ) O(MN \log C) O(MNlogC) 。 其中 N , M N,M N,M 是方格的边长。最差情况下进行 log C ( C = 1 e 6 ) \log C\ (C = 1e6) logC (C=1e6) 次二分查找,每一次二分查找最差情况下要遍历所有单元格一次,时间复杂度为 O ( M N ) O(MN) O(MN) 。
- 空间复杂度: O ( M N ) O(MN) O(MN) 。 数组 v i s vis vis 的大小为 M N MN MN ,如果使用深度优先遍历,须要使用的栈的大小最多为 M N MN MN ,如果使用广度优先遍历,须要使用的队列的大小最多为 M N MN MN 。
解法2 最小瓶颈路模型+最小生成树(Prim+堆/Kruskal+边集数组)
根据题意,我们要找的是从左上角到右下角的最优路径,其中最优路径是指途径的边的最大权重值最小,然后输出最优路径中的最大权重值。此处的边权为途径节点间高度差绝对值。
根据最小瓶颈路模型,我们可以使用Kruskal最小生成树算法:
- 先遍历所有的点,将所有的边加入集合,存储的格式为数组 [ a , b , w ] [a, b, w] [a,b,w] ,代表编号为 a a a 的点和编号为 b b b 的点之间的权重为 w w w(按照题意, w w w 为两者的高度绝对差)。
- 对边集集合进行排序,按照 w w w 进行从小到达排序。
- 当我们有了所有排好序的候选边集合之后,对边从前往后处理,选择那些不会出现环的边加入最小生成树中。
- 每次加入一条边之后,使用并查集来查询左上角点和右下角点是否连通。如果连通,那么该边的权重即是答案。
class Solution {
private class UnionFind {
private int[] parent;
public UnionFind(int n) {
parent = new int[n];
for (int i = 0; i < n; ++i) parent[i] = i;
}
public int find(int x) {
return x != parent[x] ? parent[x] = find(parent[x]) : x;
}
public boolean isConnected(int x, int y) { return find(x) == find(y); }
public void union(int p, int q) {
int rp = find(p), rq = find(q);
if (rp == rq) return;
parent[rp] = rq;
}
}
public int minimumEffortPath(int[][] grid) {
int n = grid.length, m = grid[0].length;
int len = n * m;
int[][] d = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
UnionFind unionFind = new UnionFind(len);
// 预处理所有无向边
// edge存[a,b,w]: 代表从a到b所需的时间点为w
// 虽然我们可以往四个方向移动,但只要对于每个点都添加「向右」和「向下」
// 两条边的话,其实就已经覆盖了所有边
List<int[]> edges = new ArrayList<>();
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
int index = i * m + j;
int a, b, w;
if (i + 1 < n) {
a = index; b = (i + 1) * m + j;
w = Math.abs(grid[i][j] - grid[i + 1][j]);
edges.add(new int[]{a, b, w});
}
if (j + 1 < m) {
a = index; b = i * m + (j + 1);
w = Math.abs(grid[i][j] - grid[i][j + 1]);
edges.add(new int[]{a, b, w});
}
}
}
Collections.sort(edges, (a, b) -> a[2] - b[2]); // 根据w权值升序
// 从「小边」开始添加,当某一条边应用之后,恰好使得「起点」和「结点」联通
// 那么代表找到了「最短路径」中的「权重最大的边」
int start = 0, end = len - 1;
for (int[] edge : edges) {
int a = edge[0], b = edge[1], w = edge[2];
unionFind.union(a, b);
if (unionFind.isConnected(start, end)) return w;
}
return 0;
}
}
Kruskal虽然没有求出完整最小生成树,但是对所有边进行了排序。我们可以使用Prim算法+优先队列。
下面将此问题抽象为一张带权有向图,每个单元格为顶点,有指向相邻顶点的有向边,边的权值为指向顶点的高度绝对差。然后用Prim算法,求出最小生成树上左上角的点到右下角的点的路径上的最大边权值。此时不用对所有边进行排序。
class Solution {
public int minimumEffortPath(int[][] grid) {
int n = grid.length, m = grid[0].length;
boolean[][] vis = new boolean[n][m];
// 必须将 先前加入队列时的边权重 加入int[]中
Queue<int[]> minHeap = new PriorityQueue<>((a, b) -> a[2] - b[2]);
minHeap.offer(new int[]{0, 0, 0});
int[][] dist = new int[n][m];
for (int[] row : dist)
Arrays.fill(row, Integer.MAX_VALUE);
dist[0][0] = 0;
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
while (!minHeap.isEmpty()) { // 找最短的边
int[] front = minHeap.poll();
int x = front[0], y = front[1], d = front[2];
if (vis[x][y]) continue;
vis[x][y] = true;
if (x == n - 1 && y == m - 1) break;
// 更新
for (int i = 0; i < 4; ++i) {
int u = x + directions[i][0], v = y + directions[i][1];
if (u >= 0 && u < n && v >= 0 && v < m
&& !vis[u][v] && // prim算法
Math.max(d, Math.abs(grid[x][y] - grid[u][v]))
<= dist[u][v]) {
dist[u][v] = Math.max(d,
Math.abs(grid[x][y] - grid[u][v]));
minHeap.offer(new int[]{u, v, dist[u][v]});
}
}
}
return dist[n - 1][m - 1];
}
}
复杂度分析:
- 时间复杂度: O ( M N log M N ) O(MN \log MN) O(MNlogMN) 。 使用了优先队列的 Prim 算法的时间复杂度是 O ( E log E ) O(E \log E) O(ElogE) ,这里 E E E 是边数,至多是顶点数的 4 4 4 倍,顶点数为 M N MN MN ,因此 O ( E log E ) = O ( 4 M N log M N ) = O ( M N log M N ) O(E \log E) = O(4MN \log MN) = O(MN \log MN) O(ElogE)=O(4MNlogMN)=O(MNlogMN) 。
- 空间复杂度: O ( M N ) O(MN) O(MN) 。 数组 v i s vis vis 、 d i s t dist dist 的大小为 O ( M N ) O(MN) O(MN) ,优先队列中保存的边的总数也是 M N MN MN 级别的。