线性回归例子

news2024/10/6 12:21:08

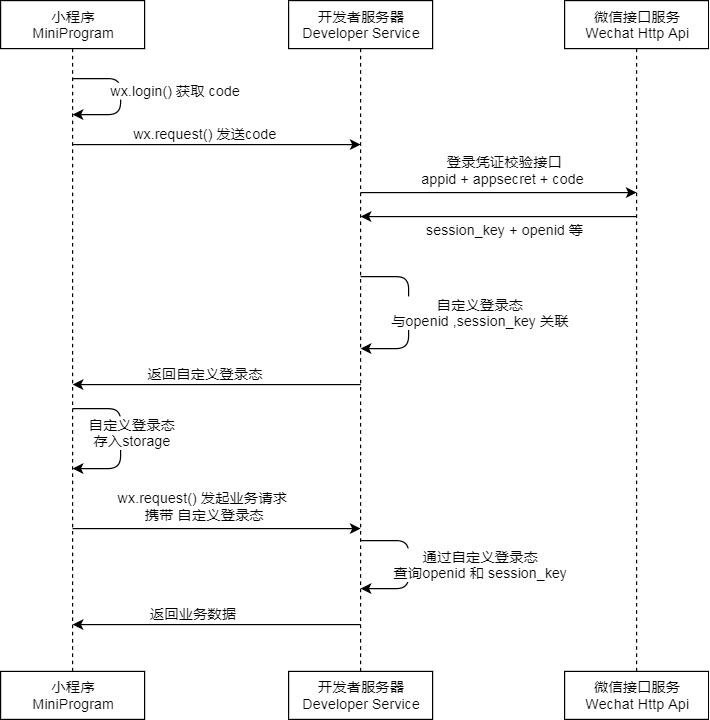
转自：https://www.cnblogs.com/BlairGrowing/p/15061912.html

刚开始接触深度学习和机器学习，由于是非全日制，也没有方向感，缺乏学习氛围、圈子，全靠自己业余时间瞎琢磨，犹如黑夜中的摸索着过河。

只是顺着原作者的思路捋一下，代码部分纯粹照搬原作者的源码。

希望自己有一天也能在黑夜中，摸着石头，跟着前行者的微弱光芒，在狂风暴雨中，坚定信息和祈祷，努力前行，也能过去人生中的大河。



import torch
from IPython import display
from matplotlib import pyplot as plt #matplotlib包可用于作图，用来显示生成的数据的二维图。
import numpy as np
import random


feature_size = 2

example_count = 10000

true_w = [8.88888888, 8.88888888]

true_b = 3.14159265

#生成特征，生成均值为0，方差为1 的特征矩阵
features = torch.tensor(np.random.normal(0, 1, (example_count, feature_size)), dtype=torch.float)

#输出特征矩阵的维度
print("特征矩阵的维度=",list(features.shape))

#根据线性方程得出特征对应的labels
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
#print(labels)

# 添加随机噪声
labels += torch.tensor(np.random.normal(0, 1, size=labels.size()), dtype=torch.float)
#print(labels)



def use_svg_display(): 
    # 用矢量图显示 
    display.set_matplotlib_formats('svg') 
    
def set_figsize(figsize=(10, 5)): 
    use_svg_display() 
    # 设置图的尺寸 
    plt.rcParams['figure.figsize'] = figsize 
    
#绘制散点图
set_figsize() 
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1);



def data_iter(batch_size, features, labels): 
    num_examples = len(features) 
    indices = list(range(num_examples)) 
    
    #print(indices)
    
    # 样本的读取顺序是随机的 
    random.shuffle(indices)  
    for i in range(0, num_examples, batch_size): 
        # 最后一次可能不足一个batch 
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) 
        yield  features.index_select(0, j), labels.index_select(0, j)
        
        

batch_sizes = 10

    
w = torch.tensor(np.random.normal(0, 1, (feature_size, 1)), dtype=torch.float32) 
b = torch.zeros(1, dtype=torch.float32)

w.requires_grad_(requires_grad=True) 
b.requires_grad_(requires_grad=True)


def lineRegression(X, w, b): 
    return torch.mm(X, w) + b


def squared_loss(y_hat, y):  
    return (y_hat - y.view(y_hat.size())) ** 2 / 2



def sgd(params, lr, batch_size): 
    for param in params: 
        param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
        
        
lr = 0.01

num_epochs = 10

net = lineRegression 

for epoch in range(num_epochs):       # 训练模型一共需要num_epochs个迭代周期 
    
    # 在每一个迭代周期中，会使用训练数据集中所有样本一次 
    for X, y in data_iter(batch_size, features, labels):       # x和y分别是小批量样本的特征和标签 
        l = squared_loss(net(X, w, b), y).sum()     # l是有关小批量X和y的损失 
        l.backward()     # 小批量的损失对模型参数求梯度 
        sgd([w, b], lr, batch_size)     # 使用小批量随机梯度下降迭代模型参数 
        w.grad.data.zero_()    # 梯度清零 
        b.grad.data.zero_() 
        
    train_l = squared_loss(net(features, w, b), labels) 
    print('epoch %d, loss %f, w %f b % f' % (epoch + 1, train_l.mean().item(), w.sum().mean(),b.sum().mean()))

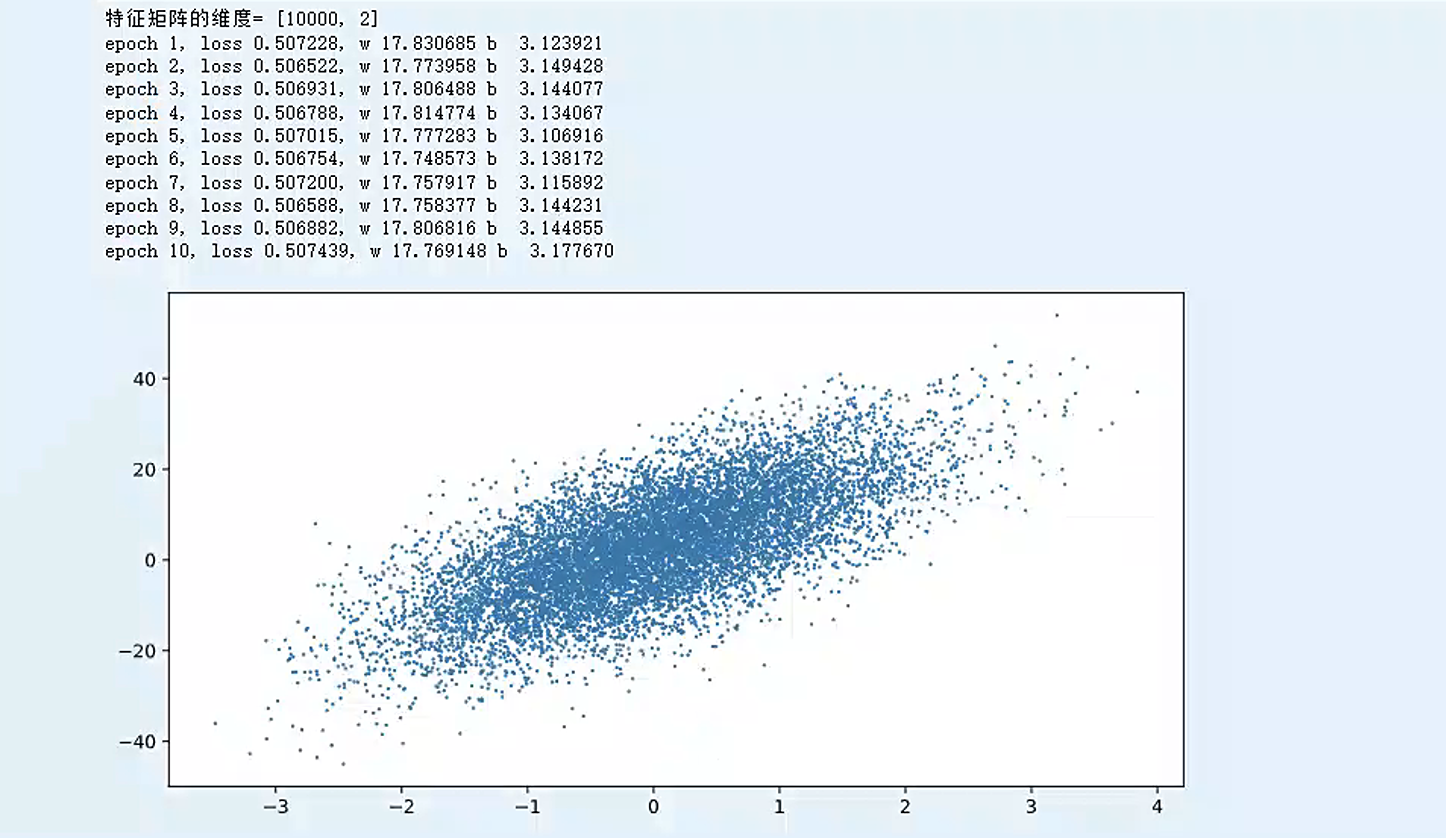
运行结果如下：

在这里插入图片描述

注意：

backward函数会计算，参与本参数运算的（包括本参数在内）其他参数的梯度。
最小二乘法可以用来计算损失，它的最小值就是梯度优化的目标位置，因此，利用梯度下降算法逐步逼近该位置，就可以拟合w和b参数，同时用它来画图表示损失，从而实现回归算法。这部分是整个回归算法的核心，明白了此处，才能真正理解回归算法的本质。
从结果可以看到，最后拟合出来的w(17.769148)和b(3.177670)跟labels中实际值w1(8.88888888) + w2 (8.88888888) = 17.77777776和3.14159265两个数字的值非常接近了，这也显示了机器学习能力的强大和魅力。而且，这还是在29行添加了误差的情况下。若是删除第29行人为添加的正态分布误差，真实数据的拟合结果如下图，误差在万分之一量级。

在这里插入图片描述