数据结构: 邻接矩阵,邻接表
1.图的存储方式:邻接矩阵,邻接表
1.稀疏图和稠密图
2.无向图:
n
n
n 个点,最多
n
(
n
−
1
)
/
2
n(n-1)/2
n(n−1)/2 条边,
当
m
m
m 接近
n
(
n
−
1
)
/
2
n(n-1)/2
n(n−1)/2 的时候是稠密图。
n
=
1000
n=1000
n=1000 ,
5050
5050
5050 条边,
m
=
10000
m=10000
m=10000 条边是稀疏图!
结论: 稀疏图用邻接表,稠密图用邻接矩阵。
3.有向图:
n
n
n 个点,最多
n
(
n
−
1
)
n(n-1)
n(n−1) 条边,
当
m
m
m 接近
n
(
n
−
1
)
n(n-1)
n(n−1) 的时候是稠密图。
n
=
1000
n=1000
n=1000 ,最多
1000000
1000000
1000000 条边,
m
=
10000
m=10000
m=10000 条边,稀疏图!
2.节点的出度与入度:
有向图:
入度:
din[1]=0;
dout[1]=2;
出度:
din[4]=1;
dout[3]=2;
让我们来练习一下:
图的存储
题目描述
给定一个 n n n 个顶点 m m m 条边的无向图。请以邻接矩阵和邻接表的形式输出这一张图。
输入格式
第一行输入两个正整数 n n n 和 m m m,表示图的顶点数和边数。
第二行开始,往后 m m m 行,每行输入两个以空格隔开的正整数 u , v u,v u,v,表示 u , v u,v u,v 顶点之间有一条边直接相连。
输出格式
首先输出 n n n 行 n n n 列的矩阵,以空格隔开每一行之间的数表示邻接矩阵。第 i i i 行第 j j j 列的数为 1 1 1 则表示顶点 i , j i,j i,j 之间有一条边直接相连;若为 0 0 0 则表示没有直接相连的边。
再往后输出 n n n 行。第 i i i 行首先先输出一个整数 d i d_i di,表示这个顶点的度数,再按照从小到大的顺序,依次输出与顶点 i i i 直接相连的所有顶点。
样例 #1
样例输入 #1
5 5
1 2
2 3
3 5
1 3
3 4
样例输出 #1
0 1 1 0 0
1 0 1 0 0
1 1 0 1 1
0 0 1 0 0
0 0 1 0 0
2 2 3
2 1 3
4 1 2 4 5
1 3
1 3
提示
样例的图如图所示:
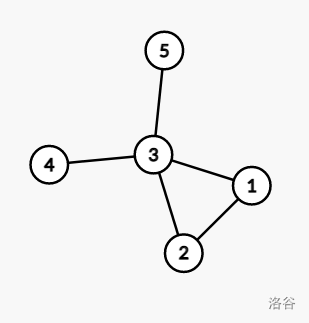
数据保证,对于所有数据, 1 ≤ n ≤ 1000 1 \leq n \leq 1000 1≤n≤1000, 1 ≤ m ≤ 1 0 5 1 \leq m \leq 10^5 1≤m≤105,且图无重边无自环。
这道题要先构建一个邻接表,再去找谁能到谁那
构建邻接表代码如下:
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
a[x][y]++;
a[y][x]++;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
printf("%d ",a[i][j]);
}
printf("\n");
}
查找代码如下:
for(int i=1;i<=n;i++)
{
printf("%d ",v[i].size());
sort(v[i].begin(),v[i].end());
for(int j=0;j<v[i].size();j++)
{
printf("%d ",v[i][j]);
}
printf("\n");
}
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N=1010,M=1e5+10;
vector<int> v[N];
int a[N][N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int j,c;
scanf("%d%d",&j,&c);
a[j][c]=1;
a[c][j]=1;
v[j].push_back(c);
v[c].push_back(j);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
printf("%d ",a[i][j]);
}
printf("\n");
}
for(int i=1;i<=n;i++)
{
printf("%d ",v[i].size());
sort(v[i].begin(),v[i].end());
for(int j=0;j<v[i].size();j++)
{
printf("%d ",v[i][j]);
}
printf("\n");
}
return 0;
}