内容摘抄自： 小而美的算法技巧：前缀和数组 | labuladong 的算法小抄

一维数组的前缀和

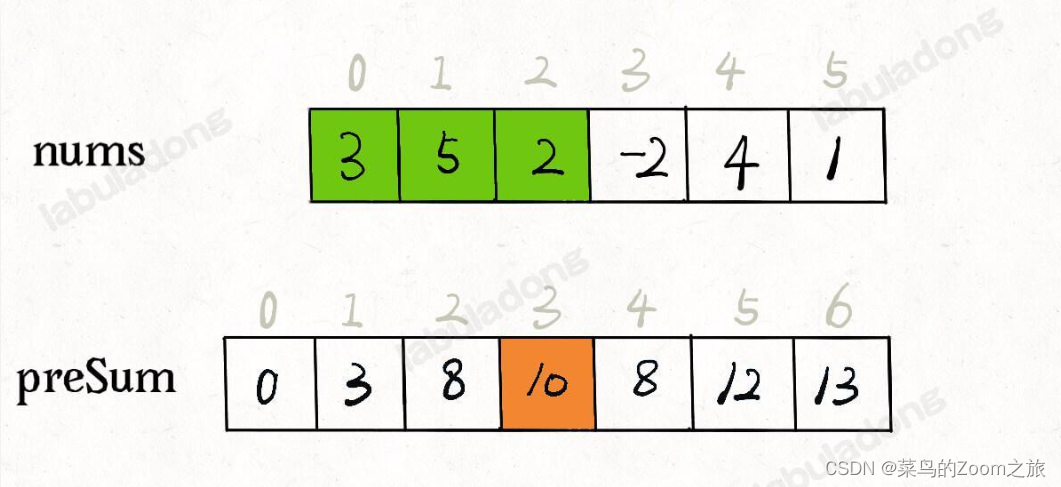
看这个 preSum 数组，若想求索引区间 [1, 4] 内的所有元素之和，
就可以通过 preSum[5] - preSum[1] 得出。

class NumArray {
    private:
        // 前缀和数组
        vector<int> preSum;
    
    public:
        /* 输入一个数组，构造前缀和 */
        NumArray(vector<int>& nums) {
            // preSum[0] = 0，便于计算累加和
            preSum.resize(nums.size() + 1);
            // 计算 nums 的累加和
            for (int i = 1; i < preSum.size(); i++) {
                preSum[i] = preSum[i - 1] + nums[i - 1];
            }
        }
        
        /* 查询闭区间 [left, right] 的累加和 */
        int sumRange(int left, int right) {
            return preSum[right + 1] - preSum[left];
        }
};

二维数组的前缀和

如leetcode 304：

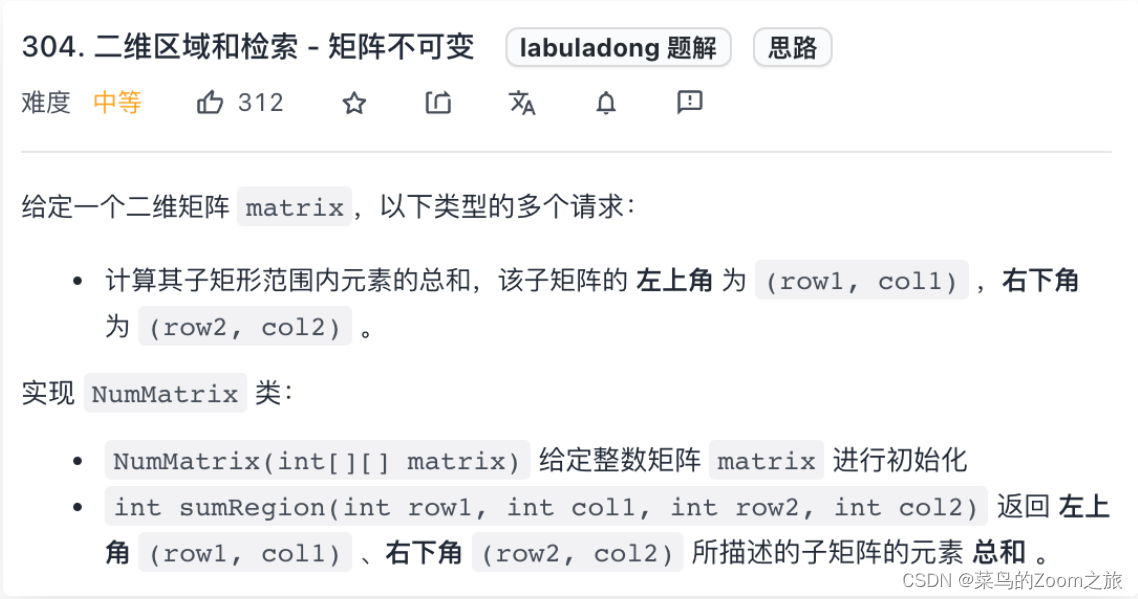
注意任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和的运算：

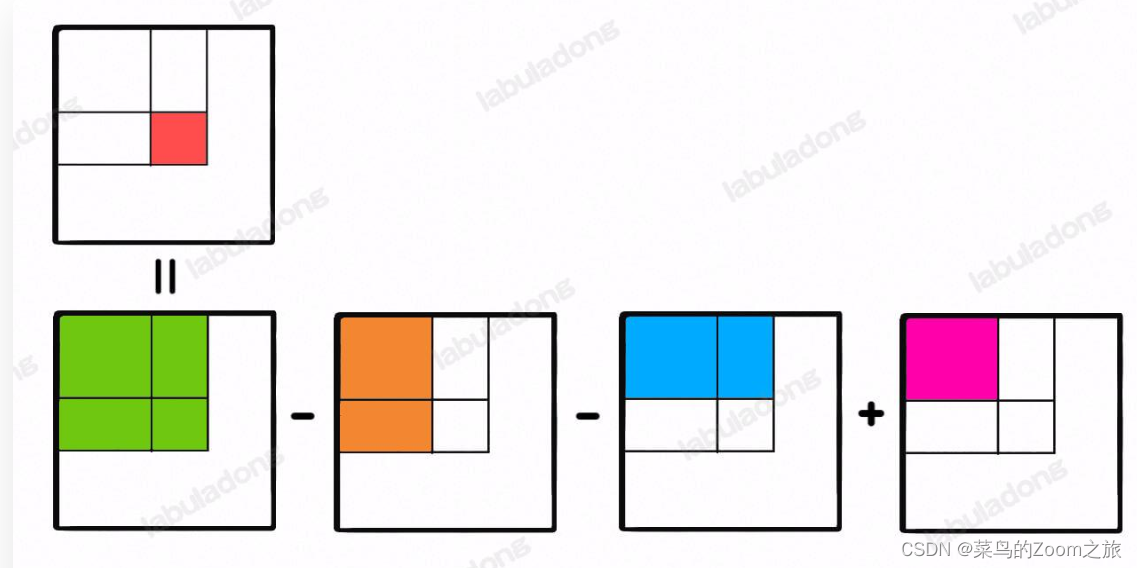
 而这四个大矩阵有一个共同的特点，就是左上角都是 (0, 0) 原点。

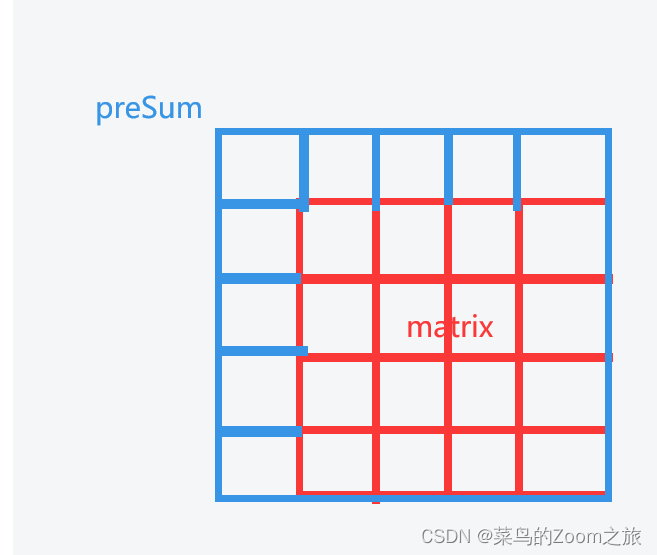
那么做这道题更好的思路和一维数组中的前缀和是非常类似的，我们可以维护一个二维 preSum 数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和：

值得注意的是 preSum数组要比matrix数组半圈，大出来的这半圈默认为值为0。
同时 再求preSum的时候 要捋清楚和matrix 索引的对应关系

class NumMatrix {
private:
    // 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    vector<vector<int>> preSum;
    
public:
    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        if (m == 0 || n == 0) return;
        // 构造前缀和矩阵
        preSum = vector<vector<int>>(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 计算每个矩阵 [0, 0, i, j] 的元素和
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
            }
        }
    }
    
    // 计算子矩阵 [x1, y1, x2, y2] 的元素和
    int sumRegion(int x1, int y1, int x2, int y2) {
        // 目标矩阵之和由四个相邻矩阵运算获得
        return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
    }
};

 笔试真题：蛋糕切割问题（切蛋糕问题）

美团0812秋招笔试真题解析

// 小美切蛋糕.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include <iostream>
#include <vector>
using namespace std;

class Solution
{
public:
	Solution(vector<vector<int>>& a)
	{
		int n = a.size(); //行
		int m = a[0].size();   //列
		if (!n && !m) return;
		//构造前缀和数组
		preSum = vector<vector<int>>(n + 1, vector<int>(m + 1, 0));
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= m; j++)
				//计算每一个矩阵[0,0,i,j]的元素和
				preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] + a[i-1][j-1] - preSum[i - 1][j - 1];

	}

	int sumRegion(int x1, int y1, int x2, int y2)
	{
		return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
	}

	int getMin(vector<vector<int>>& a)
	{
		int n = a.size();
		int m = a[0].size();
		int res = INT_MAX;

		for (int i = 0; i < m; i++)
		{
			//0,0,n-1,j     0,j,n-1,m-1
			res = min(res, abs(sumRegion(0, 0, n - 1, i) - sumRegion(0, i, n - 1, m - 1)));
		}
		return res;
	}


private:

	//preSum[i][j]用于记录a中子矩阵的元素和
	vector<vector<int>> preSum;

};



int main()
{
	int n, m;
	cin >> n >> m;
	vector<vector<int>> a(n, vector<int>(m, 0));

	for (int i = 0; i < n; i++)
		for (int j = 0; j < m; j++)
		{
			cin >> a[i][j];
		}
	Solution MySolution(a);
	cout<< MySolution.getMin(a) << endl;

}