图论——最短路算法

news2025/2/25 13:49:42

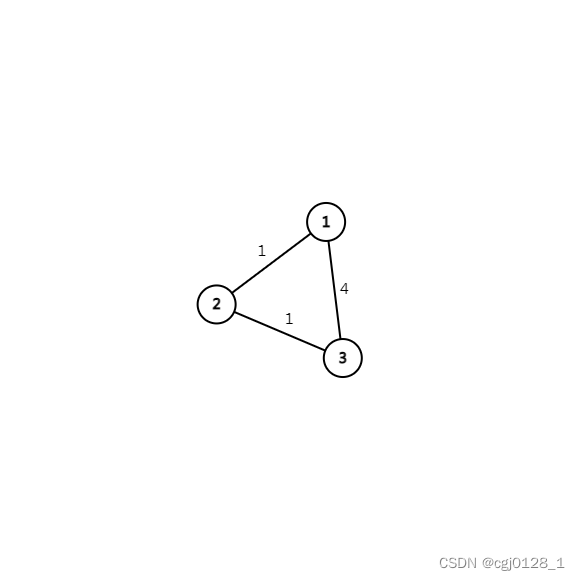
引入：

如上图，已知图G。

问节点1到节点3的最短距离。

可心算而出为d[1,2]+d[2,3]=1+1=2,比d[1,3]要小。

求最短路径算法：

1.Floyd(弗洛伊德)

是一种基于三角形不等式的多源最短路径算法。边权可以为负数

表现为a[i,j]+a[j,k]<a[i,k]。

算法思想：

枚举“中转站”(k),“起点”(i),“终点”(j)

设d[i,j]为由i点到j点的最短路径

则 $d[i,j]=min(d[i,j],d[i,k]+d[k,j])$

初始化d[i,j]为无穷大（ $1\leq i\leq n,1\leq j\leq n$ ）

算法模板如下：

inline int Floyd(int n,int st,int ed)// n个点，起点st,终点ed,返回st到ed的最短距离
{
    int d[n][n];
    memset(d,0x3f,sizeof(d));
    for(int i=1;i<=n;i++) d[i][i]=0;
    for(int k=1;k<=n;k++)
    {
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
            }
        }
    }
    return d[st][ed];
}

补充：Floyd输出最短路径。

题目：有向图中任意两点最短路径（floyd）

题目描述

　　一个含n个结点的有向图（注意：是有向图！！），以矩阵存储方式给出，请求出指定的多组两个点之间的最短距离及其最短路径。

输入输出格式

输入格式：

　　第1行，一个整数n（0 < n < 300 ），表示有向图中结点的个数。
　　第2行到第（n+1）行，是一个n*n的矩阵，表示无向图中各结点之间的联结情况，矩阵中的数据为小于1000的正整数，其中 -1 表示无穷大！！
　　第（n+2）行，一个整数m，表示接下来有m组顶点 < i , j >对，其中，i是起点，j是终点，且i不等于j。
　　接下来有m行，每行两个整数，中间一个空格间隔，分别表示i和j，表示求解i点到j点的最短距离及最短路径。

　　注：输入数据已经确保答案每一组顶点间的最短路径是唯一的，无多解数据存在，顶点编号用数字表示，从1开始编号，至n结束！

输出格式：

　　共 2m 行。
　　第(m-1)*2+1行，一个整数，表示第m组顶点的最短距离，若两点间距离为无穷大，则输出 -1。
　　第(m-1)*2+2行，用顶点编号表示的路径序列，各顶点编号间用一个空格间隔，表示第m组顶点的最短路径，若两点间距离为无穷大，则输出的路径序列为 -1。

输入输出样例

输入样例#1：

3
0 4 11
6 0 2
3 -1 0
2
2 1
3 2

输出样例#1：

5
2 3 1
7
3 1 2

代码如下：

#include<bits/stdc++.h>
using namespace std;
int n,q;
int d[10001][10001],pre[10001][10001];
void dg(int i,int j)
{
	if(i==j||pre[i][j]==0) return;
	int k=pre[i][j];
	dg(i,k);
	dg(k,j);
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>d[i][j];
			if(d[i][j]==-1)
			{
				d[i][j]=0x7fffff;
			}
		}
	}
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(d[i][k]+d[k][j]<d[i][j])
				{
					d[i][j]=d[i][k]+d[k][j];
					pre[i][j]=k;
				}
			}
		}
	}
	cin>>q;
	for(int i=1;i<=q;i++)
	{
		int x,y;
		cin>>x>>y;
		cout<<d[x][y]<<endl;
		cout<<x<<" ";
		dg(x,y);
		cout<<y;
		cout<<endl;
	}
	return 0;
}

传递闭包（连通性）

$d[i,j]=d[i,j]|(d[i,k]&d[k,j])$
d[i,j]表示i与j是否连通。

题目：刻录光盘

题目描述

　　在FJOI2010夏令营快要结束的时候，很多营员提出来要把整个夏令营期间的资料刻录成一张光盘给大家，以便大家回去后继续学习。组委会觉得这个主意不错！可是组委会一时没有足够的空光盘，没法保证每个人都能拿到刻录上资料的光盘，怎么办呢？！

　　DYJ分析了一下所有营员的地域关系，发现有些营员是一个城市的，其实他们只需要一张就可以了，因为一个人拿到光盘后，其他人可以带着U盘之类的东西去拷贝啊！

　　他们愿意某一些人到他那儿拷贝资料，当然也可能不愿意让另外一些人到他那儿拷贝资料，这与我们FJOI宣扬的团队合作精神格格不入！！！

　　现在假设总共有N个营员（2<=N<=200），每个营员的编号为1~N。DYJ给每个人发了一张调查表，让每个营员填上自己愿意让哪些人到他那儿拷贝资料。当然，如果A愿意把资料拷贝给B，而B又愿意把资料拷贝给C，则一旦A获得了资料，则B，C都会获得资料。

　　现在，请你编写一个程序，根据回收上来的调查表，帮助DYJ计算出组委会至少要刻录多少张光盘，才能保证所有营员回去后都能得到夏令营资料？

输入输出格式

输入格式：

先是一个数N，接下来的N行，分别表示各个营员愿意把自己获得的资料拷贝给其他哪些营员。即输入数据的第i+1行表示第i个营员愿意把资料拷贝给那些营员的编号，以一个0结束。如果一个营员不愿意拷贝资料给任何人，则相应的行只有1个0，一行中的若干数之间用一个空格隔开。

输出格式：

一个正整数，表示最少要刻录的光盘数。

输入输出样例

输入样例#1：

5
2 4 3 0
4 5 0
0
0
1 0

输出样例#1：

代码：

#include<bits/stdc++.h>
using namespace std;
int f[100001],d[300][300],g[100001],ans;
int main()
{
	int n;
	cin>>n;
	memset(d,0x3f,sizeof(d));
	for(int i=1;i<=n;i++)
	{
		f[i]=i;
	}
	for(int i=1;i<=n;i++)
	{
		int x;
		while(1)
		{
			cin>>x;
			if(x==0) break;
			d[i][x]=1;
		}
	}
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(i!=j&&j!=k&&k!=i)
				{
					if(d[i][k]==1&&d[k][j]==1)
					{
						d[i][j]=1;
					}
				}
			}
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(d[i][j]==1)
			{
				f[j]=f[i];
			}
		}
	}
	for(int i=1;i<=n;i++) 
	{
		if(f[i]==i) 
		{
			ans++;
		}
	}
	cout<<ans;
	return 0;
}

2.dijkstra（狄克斯特拉，迪杰斯特拉）

基于贪心的单源最短路径算法。边权必须为正数

基本思想：

设d[i]为起点s到终点i的最短路径,a[i,j]为点i到点j边权。

1.找 $min\begin{Bmatrix} d[i] \end{Bmatrix}\left ( 1\leqslant i\leqslant n ,vis[i]=true \right )$ ,并将其用k记录

2. $vis[k]=true$

3. $d[i]=min\begin{Bmatrix} d[i],d[k]+a[k][i] \end{Bmatrix}\left ( 1\leqslant i\leqslant n \right )$ 松弛操作，用k来更新图中所有点。

int dijkstra(int n,int st,int ed)
{
    int dis[n+1],vis[n+1];
    memset(dis,0x3f,sizeof(dis));
    memset(vis,0,sizeof(vis));
    dis[st]=0;
    for(int i=1;i<=n;i++)
    {
        int k,minn=0x7fffff;
        for(int j=1;j<=n;j++)if(!vis[j]&&dis[j]<minn) minn=dis[j],k=j;
        vis[k]=true;
        for(int j=1;j<=n;j++) d[j]=min(d[j],d[k]+a[k][j]);
    }
    return d[ed];
}

堆优化dijkstra:

typedef pair<int,int> P;
struct node{
	int to;
	int next;
	int w;
}edge[10000010];
int head[10000010],d[10000010];
int cnt;
int n,m,x,y,z,s;
void add_edge(int u,int v,int w)
{
	edge[cnt].to=v;
	edge[cnt].w=w;
	edge[cnt].next=head[u];
	head[u]=cnt++;
}
void dijkstra(int s)
{
	priority_queue< P,vector<P>,greater<P> >q;
	memset(d,0x3f,sizeof(d));
	d[s]=0;
	q.push(P(0,s));
	while(!q.empty())
	{
		P p=q.top();
		q.pop();
		int u=p.second;
		if(d[u]<p.first) continue;
		for(int i=head[u];i!=-1;i=edge[i].next)
		{
			int v=edge[i].to;
			if(d[v]>d[u]+edge[i].w)
			{
				d[v]=d[u]+edge[i].w;
				q.push(P(d[v],v));
			}
		}
	}
}

3.Bellman-Ford

O(n*m) 但有更优的，由其转换而来的Spfa算法，不再赘述。边权可以为负数

4.Spfa

基于bellman-Ford，用队列优化的单源最短路径算法，边权可以为负数，可用于判断负环。

代码如下：

    int head=0,tail=1;
	team[1]=s,vis[s]=1,dis[s]=0;
	while(head<tail)
	{
		head=(head+1)%10000;
		int u=team[head];
		vis[u]=0;
		for(int i=1;i<=len[u];i++)
		{
			int v=le[u][i];
			if(dis[v]>dis[u]+a[u][v])
			{
				dis[v]=dis[u]+a[u][v];
				if(vis[v]==0)
				{
					tail=(tail+1)%10000;
					team[tail]=v;
					vis[v]=1;
				}
			}
		}
	}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/870106.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！