文章目录
- 定义
- Tarjan求e-DCC
- Tarjan求v-DCC
- 395. 冗余路径
- 1183. 电力
- 396. 矿场搭建
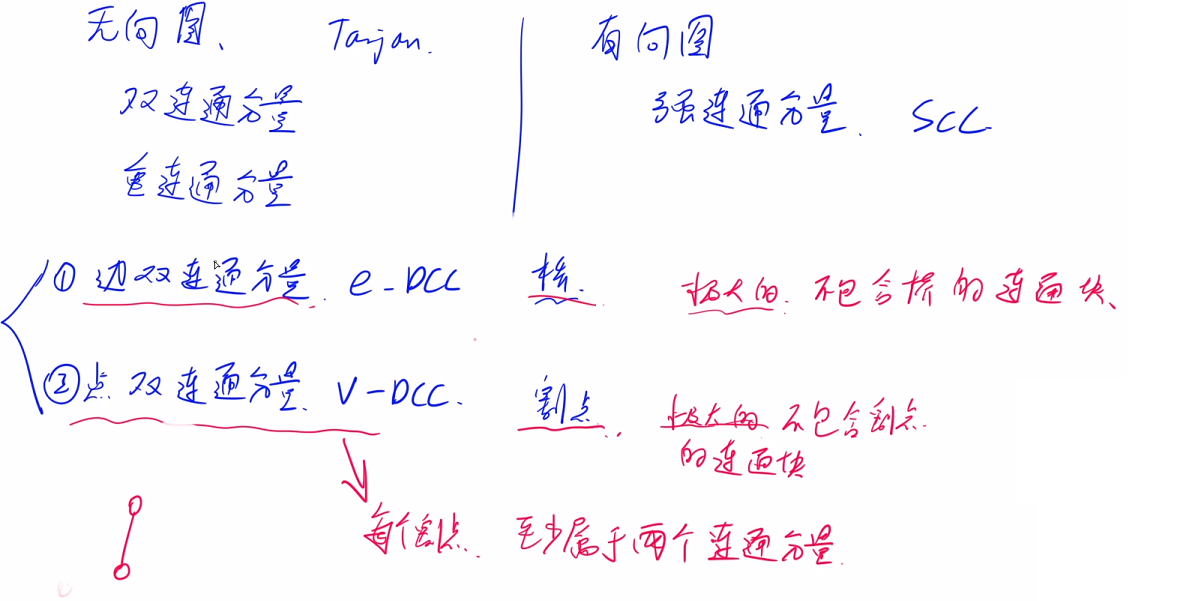
定义
无向图有两种双连通分量
- 边双连通分量,e-DCC
- 点双连通分量,v-DCC
桥:删除这条无向边后,图变得不连通,这条边被称为桥
边双连通分量:极大的不含有桥的连通区域,说明无论删除e-DCC中的哪条边,e-DCC依旧连通 (该连通分量的任意边属于原图中的某条环)。此外,任意两点之间一定包含两条不相交(无公共边)的路径
割点:删除该点(与该点相关的边)后,图变得不连通,这个点被称为割点
点双连通分量:极大的不含有割点的连通区域
一些性质:
- 每个割点至少属于两个连通分量
- 任何两个割点之间的边不一定是桥,任何桥两边的端点不一定是割点,两者没有必然联系,一个点连通分量也不一定是边连通分量
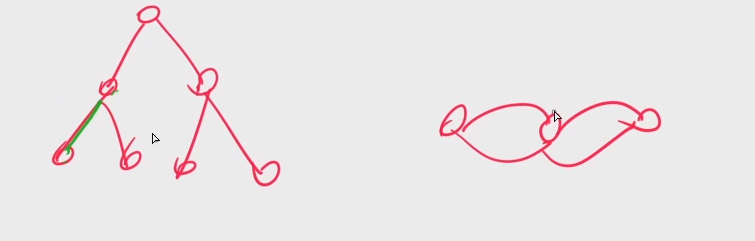
Tarjan求e-DCC
无向图不存在横叉边
和有向图的强连通分量类似,引入dfn和low两个数组
如何找到桥?判断x->y的y是否能走到x之前(祖先节点),如果能走到,x和y在一个环中,删除这条边,其他点依然是连通的
所以x->y为桥:dfn[x] < low[y]
如何找到所有边的双连通分量?
- 删除所有桥
- 或者用stk辅助,若
dfn[x] == low[x],说明x出发一定走不到x的祖先节点,那么x和其父节点之间的边是桥,此时还在stk中的点为e-DCC的节点
这里使用第二种方式,模板:
void tarjan(int x, int from)
{
dfn[x] = low[x] = ++ tp;
stk[ ++ tt] = x;
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (!dfn[y])
{
tarjan(y, i);
low[x] = min(low[x], low[y]);
}
else if (i != (from ^ 1))
low[x] = min(low[x], dfn[y]);
if (dfn[x] < low[y])
st[i] = st[i ^ 1] = true;
}
if (dfn[x] == low[x])
{
int y;
cnt ++ ;
do {
y = stk[tt -- ];
id[y] = cnt;
} while (x != y);
}
}
由于无向图要存储两条有向边,并且从数组的0下标开始存储,所以0,1、2,3…这样一对的边是互相反向的边,即i和i ^ 1为反向边
为什么与有向图的强连通分量不同,边双连通分量不需要使用st数组以标记栈中的元素?
因为无向图不存在横叉边的概念,就不会出现:x->y而y的dfn小于x,因为在无向图中y一定会向x遍历
Tarjan求v-DCC
如何求割点?low[y] >= dfn[x],删除x节点后,y就是一颗独立的子树
- 如果x不是根节点,那么x是一个割点
- 如果x是根节点,至少有两个y满足以上关系
求割点的板子:
void tarjan(int x)
{
dfn[x] = low[x] = ++ tp;
int t = 0;
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x]) t ++ ;
}
else low[x] = min(low[x], dfn[y]);
}
if (x != root) t ++ ;
ans = max(ans, t);
}
将每个v-DCC向其包含的割点连一条边
缩点后,边的数量不会增加,点的数量可能会增加到两倍
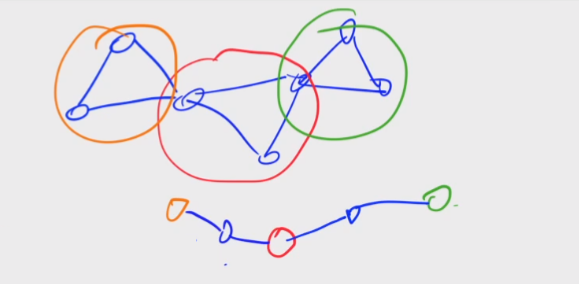
tarjan求v-DCC与割点的板子:
一个孤立的点也是一个v-DCC,这里需要特判
若满足条件:low[y] >= dfn[x],那么y的子树与x一起就是一个v-DCC
对于该节点是否是割点还需要特判,若该节点为根,并且与该节点相连的连通块数量为1,那么该节点就不是一个割点
void tarjan(int x)
{
dfn[x] = low[x] = ++ tp;
stk[ ++ tt ] = x;
if (x == root && h[x] == -1)
{
++ dcnt;
dcc[dcnt].push_back(x);
return;
}
int t = 0; // 与x相连的连通块数量
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x])
{
dcnt ++, t ++ ;
if (x != root || t > 1) st[x] = true; // x为割点
int u;
do {
u = stk[tt -- ];
dcc[dcnt].push_back(u);
} while (u != y);
dcc[dcnt].push_back(x);
}
}
else low[x] = min(low[x], dfn[y]);
}
}
395. 冗余路径
395. 冗余路径 - AcWing题库
任意两点间都存在两条没有重复边的路径,等价于整个图是一个双连通分量
将无向连通图的边双连通分量缩点后,得到的结构是一颗树,因为边双连通分量是不包含桥的结构,缩点后,图中只含有桥,即删除任意一条边后,图成为两个连通块,这是一个树结构
为了满足题意,需要向这颗树中添加边,使之成为边连通分量,那么要加几条边?
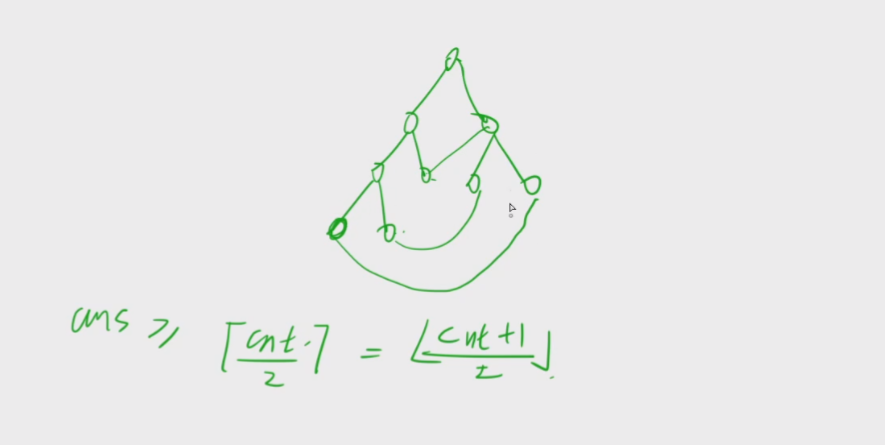
连接所有叶子节点,使这颗树结构成为双连通分量,至少需要加 [ ( c n t + 1 ) / 2 ] [(cnt + 1) / 2] [(cnt+1)/2]然后再下取整的边数,也就是将每个叶子节点相连,使环满足双连通分量的性质
注意cnt为1时需要特判
#include <iostream>
#include <cstring>
using namespace std;
const int N = 5010, M = 10010;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int stk[N], tt, id[N];
bool st[N]; int d[N];
int n, m;
void add(int x, int y)
{
e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}
void tarjan(int x, int from)
{
dfn[x] = low[x] = ++ tp;
stk[ ++ tt] = x;
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (!dfn[y])
{
tarjan(y, i);
low[x] = min(low[x], low[y]);
if (dfn[x] < low[y])
st[i] = st[i ^ 1] = true;
}
else if (i != (from ^ 1))
low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x])
{
int y;
cnt ++ ;
do {
y = stk[tt -- ];
id[y] = cnt;
} while (x != y);
}
}
int main()
{
memset(h, -1, sizeof(h));
scanf("%d%d", &n, &m);
int x, y;
for (int i = 0; i < m; ++ i )
{
scanf("%d%d", &x, &y);
add(x, y), add(y, x);
}
tarjan(1, -1);
for (int i = 0; i < idx; i ++ )
if (st[i])
d[id[e[i]]] ++ ;
int res = 0;
for (int i = 1; i <= cnt; ++ i )
if (d[i] == 1) res ++ ;
if (cnt == 1) puts("0");
else printf("%d\n", (res + 1) / 2);
return 0;
}
debug:^的优先级小于!=
可以不使用st数组标记桥:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 5010, M = 10010;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int stk[N], tt, id[N];
int d[N];
int n, m;
void add(int x, int y)
{
e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}
void tarjan(int x, int from)
{
dfn[x] = low[x] = ++ tp;
stk[ ++ tt] = x;
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (!dfn[y])
{
tarjan(y, i);
low[x] = min(low[x], low[y]);
}
else if (i != (from ^ 1))
low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x])
{
int y;
cnt ++ ;
do {
y = stk[tt -- ];
id[y] = cnt;
} while (x != y);
}
}
int main()
{
memset(h, -1, sizeof(h));
scanf("%d%d", &n, &m);
int x, y;
for (int i = 0; i < m; ++ i )
{
scanf("%d%d", &x, &y);
add(x, y), add(y, x);
}
tarjan(1, -1);
for (int x = 1; x <= n; ++ x )
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
int a = id[x], b = id[y];
if (a != b) d[a] ++ ;
}
int res = 0;
for (int i = 1; i <= cnt; i ++ )
if (d[i] == 1) res ++ ;
if (cnt == 1) puts("0");
else printf("%d\n", (res + 1) / 2);
return 0;
}
1183. 电力
1183. 电力 - AcWing题库
枚举所有割点,判断删除哪个割点后剩余的连通块数量最大
剩余的连通块数量为ans + cnt - 1
由于题目给定的图并不是一个连通图,所以可能存在多个连通块,cnt为连通块数量
枚举所有割点只能在一个连通块中枚举,此时其他连通块的数量为cnt - 1
又因为ans为删除割点后,剩余连通块最多的值,所以答案为ans + cnt - 1
这题的点编号从0开始
#include <iostream>
#include <cstring>
using namespace std;
const int N = 10010, M = 30010;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int ans, n, m, root;
void add(int x, int y)
{
e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}
void tarjan(int x)
{
dfn[x] = low[x] = ++ tp;
int t = 0;
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x]) t ++ ;
}
else low[x] = min(low[x], dfn[y]);
}
if (x != root) t ++ ;
ans = max(ans, t);
}
int main()
{
while (scanf("%d%d", &n, &m), n | m)
{
memset(h, -1, sizeof(h));
memset(dfn, 0, sizeof(dfn));
idx = tp = cnt = ans = 0;
int x, y;
for (int i = 0; i < m; ++ i )
{
scanf("%d%d", &x, &y);
add(x, y), add(y, x);
}
for (root = 0; root < n; ++ root)
{
if (!dfn[root])
{
cnt ++ ;
tarjan(root);
}
}
printf("%d\n", ans + cnt - 1);
}
return 0;
}
debug:dfn数组没有置空
396. 矿场搭建
396. 矿场搭建 - AcWing题库


对于图中的每个连通块,分情况讨论:
- 若连通块无割点,那么任意设置两个救援点即可
- 若连通块中有割点,缩点:将每个割点依然看成一个点,将每个v-DCC向其包含的割点连线
- 缩点后得到一棵树,对于叶子节点,需要建立救援点。因为只有一个点与其相连,若该点坍塌,需要在内部建立救援点。假设内部节点数量为cnt,方案数为cnt-1个,去除割点
- 对于非叶子节点,无需建立救援点,因为无论与之相连的哪个割点坍塌,该节点都能走到叶子节点,而叶子节点已经建立救援点
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
typedef unsigned long long ULL;
const int N = 1010, M = 1010;
int h[N], e[M], ne[M], idx;
vector<int> dcc[N];
int dcnt, root;
int dfn[N], low[N], tp;
int stk[N], tt;
bool st[N];
int n, m;
void add(int x, int y)
{
e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}
void tarjan(int x)
{
low[x] = dfn[x] = ++ tp;
stk[ ++ tt ] = x;
if (x == root && h[x] == -1)
{
dcnt ++ ;
dcc[dcnt].push_back(x);
return;
}
int t = 0;
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x])
{
t ++, dcnt ++ ;
if (x != root || t > 1) st[x] = true;
int u;
do {
u = stk[tt -- ];
dcc[dcnt].push_back(u);
} while (u != y);
dcc[dcnt].push_back(x);
}
}
else low[x] = min(low[x], dfn[y]);
}
}
int main()
{
int T = 1;
while (scanf("%d", &m), m)
{
for (int i = 0; i < N; ++ i ) dcc[i].clear();
memset(h, -1, sizeof(h));
memset(dfn, 0, sizeof(dfn));
memset(st, false, sizeof(st));
tp = dcnt = idx = tt = n = 0;
for (int i = 0; i < m; ++ i )
{
int x, y;
scanf("%d%d", &x, &y);
add(x, y), add(y, x);
n = max(n, x), n = max(n, y);
}
for (root = 1; root <= n; ++ root )
if (!dfn[root]) tarjan(root);
ULL sum = 1; int ans = 0;
for (int i = 1; i <= dcnt; ++ i )
{
int t = 0;
for (int j = 0; j < dcc[i].size(); ++ j )
if (st[dcc[i][j]])
t ++ ;
if (t == 0)
{
if (dcc[i].size() > 1) ans += 2, sum *= ((ULL)dcc[i].size() * (dcc[i].size() - 1)) / 2;
else ans ++ ;
}
else if (t == 1) ans += 1, sum *= (dcc[i].size() - 1);
}
printf("Case %d: %d %llu\n", T ++ , ans, sum);
}
return 0;
}
debug:由于多组测试数据,没有初始化干净所有元素
最后统计救援点数量以及方案总数时,没有对孤立点进行特判
![[内网渗透]CFS三层靶机渗透](https://raw.githubusercontent.com/leekosss/photoBed/master/202308121900810.png)