一、研究方向
建立传染病的数学模型描述传染病的传播过程
分析感染人数的变化规律,预测传染病高峰的到来
探索控制、根除、预防传染病传播蔓延的手段
二、舱室
流行病学中的一大类模型,称为“舱室”模型,它是将人群分成若干个“舱室”,各个舱室之间会有转移率(变化率),用数学模型语言来描述整个系统,就得到一个微分方程组,但往往是没有解析解的,这就需要利用 MATLAB 进行数值求解。
S (Susceptible)易感者:指缺乏免疫能力健康人,与感染者接触后容易受到感染;
E (Exposed)暴露者:指接触过感染者但暂无传染性的人,可用于存在潜伏期的传染病;
I (Infectious)感染者:指有传染性的病人,可以传播给 S,将其变为 E 或 I;
R (Recovered)治愈者:指治愈后具有免疫力的人,如终身免疫性传染病,则不会再变为 S、E 或 I,如果免疫期有限,就可以重新变为 S 类,进而可被感染。
参数
时间:一般考虑离散时间,以天为最小时间单位。
t 时刻各类人群占总人口的比例分别记为 S(t), E(t), I(t), R(t) ;各类人数所占初始比率为 S(0), E(0), I(0), R(0),分别简记为S_0, E_0, I_0, R_0.
接触数 λ:每个感染者每天有效接触的易感者的平均人数;
发病率 δ:每天感染成为感染者的暴露者占暴露者总数的比例;
治愈率 μ:每天被治愈的感染者人数占感染者总数的比例;
平均传染期 1/μ:从感染到治愈的平均天数;
传染期接触数σ=λ/μ:每个感染者在整个传染期内,有效接触的易感者人数。
一、SI模型
考虑总人口由感染者(I)和易感者(S)两类人群构成,记 S(t) 为 t 时刻易感者占总人口的比例,I(t) 为 t 时刻感染者占总人口的比例,则 S(t)+I(t)=1.
SI 模型最简单,适合不会反复发作的传染病。
1.模型假设
假设1: 假设人群中个体分布均匀;
假设2: 假设人口总数足够大,只考虑传播过程中的平均效应,即函数 S(t) 和 I(t) 可以视为连续且可微的;
假设3: 假设每个感染者每天“有效接触”的易感者人数为常数 λ,且一旦接触易感者立即被感染变为感染者,称为感染数 λ,反映本地区的卫生防疫水平;
假设4: 不考虑出生与死亡,以及人群的迁入迁出因素,即假设所考察地区总人口 N 保持不变,这不适合长期传染病。

2.模型建立
根据假设 3,每个感染者每天的有效接触人数为 λS(t), 从而全部感染者 N∙I(t) 每天有效接触的易感者人数为 N∙I(t)∙λS(t), 这些易感者立即被感染成为感染者,故在Δt 时间内新增加的感染者人数为:
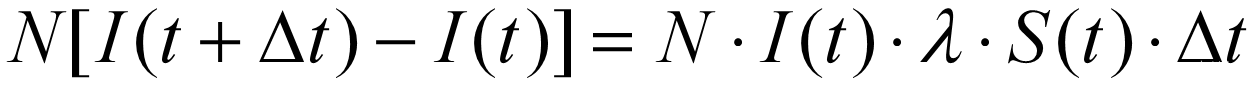
两边同除以 NΔt,考虑连续变化,令 Δt→0,则得到 SI 模型:
 3.模型求解
3.模型求解
该微分方程,也是我们熟悉的 Logistic 人口模型(总容纳量为 1),利用分离变量法可求得 SI 模型的解析解为:

用 SI 模型可以预报传染病暴发早期,患病人数的发展规律,并估算传染高峰到来的时间。
1)MATLAB求解
syms I(t) lambda I0%声明这些数为常数,不是变量
eqn= diff(I,t) ==lambda * I * (1-I);%dI/dt
cond = I(0) == I0;%初值
Isol(t) = dsolve(eqn, cond)%求解微分方程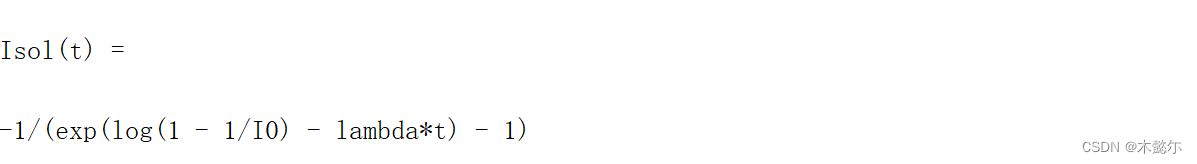
2)取一组参数 λ=5, I_0=0.1,来考察传染病的传播规律(实际中是根据真实数据估计这些参数值)
计算 MATLAB 表达式 - MATLAB eval - MathWorks 中国
syms I(t) lambda I0%声明这些数为常数,不是变量
eqn= diff(I,t) ==lambda * I * (1-I);%dI/dt
cond = I(0) == I0;%初值
Isol(t) = dsolve(eqn, cond)%求解微分方程
lambda = 5;%给予常数实际值
I0 = 0.1;
Isol(t) = eval(Isol(t));%使用eval函数可以执行文本中的 MATLAB 表达式
ts = 0:0.01:2;
plot(ts, Isol(ts))
hold on%hold on主要是用于添加新绘图的时候保留当前绘图(保留上述微分方程解析解所绘图)
line=refline(0,1)%加一条参考线,在当前坐标区中添加一条具有斜率 m 和截距 b 的参考线。
line.Color = 'r';
axis([0 2 0 1.1]);
xlabel('时间'), ylabel('感染比例');
3) 当 I(t)=0.5 时,传染速度达到最大值,反解出该时刻 t_m:

当 t=t_m时,疫情最为猛烈,病人增加的速度最快。显然 t_m 与 λ 成反比,而 λ 为疾病的传染率,它反映了当地的医疗卫生水平, λ 越小,医疗卫生水平越高。所以改善保健设施,提高医疗卫生水平,降低 λ 值就可以推迟传染高潮的到来。
将参考线添加到绘图中 - MATLAB refline - MathWorks 中国
求解优化问题或方程问题 - MATLAB solve - MathWorks 中国
(13条消息) matlab中diff咋用,给我解释一下matlab中的diff函数_梓矜的博客-CSDN博客
dI = diff(Isol,1);
tm = solve(Isol(t)==0.5, t);%将t视为未知数求解,求解t的值代入tm
eval(tm)%将tm转化成matlab可以理解的形式
figure%创建图窗
plot(ts, dI(ts), tm, dI(tm), 'r*')
xlabel('时间'), ylabel('感染速度');SI 模型的解为 Logistic 增长曲线,患者比率 I(t) 从 I(0) 迅速上升,通过曲线的拐点后上升变缓。 该模型的缺陷是显而易见的:当 t→+∞ 时,I(t)→1,这表明本地区最后所有人都会被感染。出现这种结果的原因是假设系统中只有两种人,即感染者和易感者,而未考虑感染者会被治愈的情况。
延申: SIS 模型
有些传染病如伤风、痢疾等,虽然可以治愈,但治愈后基本上没有免疫力,于是患者愈后又变成易感者,这就是 SIS 模型。
SIS 模型只需在 SI 模型假设的基础上,增加一条假设:
假设 5:患者每天被治愈的人数比例为常数 μ(治愈率)
1.模型假设
SIS 模型的人群转移规律如下:

根据假设5,每天新增加的感染者人数 N∙I(t)∙λ∙S(t),应该减去每天治愈的感染者人数为 N∙I(t)∙μ,同除以 N 得到

考虑连续变化,变成微分方程:

于是得到 SIS 模型为

若令 σ=λ/μ 表示一个感染者在整个感染期内有效接触的平均人数,称为传染期接触数。将 σ 代入上述方程中,得到 SIS 模型的另一种形式:

仍然可用分离变量法求得 SIS 模型的解析解:

1) 用 MATLAB 求 SIS 模型解析解
若记 K=1−1/σ,其实,就是 Logistic 人口模型的容纳量。
syms I(t) lambda I0 K% K = 1 - 1/ sigma
eqn = diff(I,t) == lambda * I * (K - I);
cond = I(0) == I0;
Isol(t) = dsolve(eqn, cond)

2) 传染病初期,感染率很小,不妨设 I_0<1−1/σ
若 σ>1 则 K>0,SIS 模型仍是 Logistic 人口模型,I(t) 呈 Logistic 曲线上升,当 t→+∞ 时,I(t)→1−1/σ.
取 λ=5, I_0=0, σ=5,对应 K=0.8,来考察传染病的传播规律:
(13条消息) subs函数_极客字节的博客-CSDN博客
Isol(t) = eval(Isol(t));
ts = 0:0.01:2;
plot(ts, Isol(ts))
hold on
line1 = refline(0, 1);
line1.LineStyle = '--';
line = refline(0, 1-1/sigma);
line.Color = 'r';
axis([0 2 0 1.1])
xlabel('时间'), ylabel('感染比例')
当 I(t)=1/2K=0.4 时,传染速度达到最大值,反解出该时刻:
dI = diff(Isol,1);
tm = solve(Isol(t) == K/2, t);
eval(tm)
figure
plot(ts, dI(ts), tm, dI(tm), 'r*')
xlabel('时间'), ylabel('感染速度')
axis([0 2 0 1])
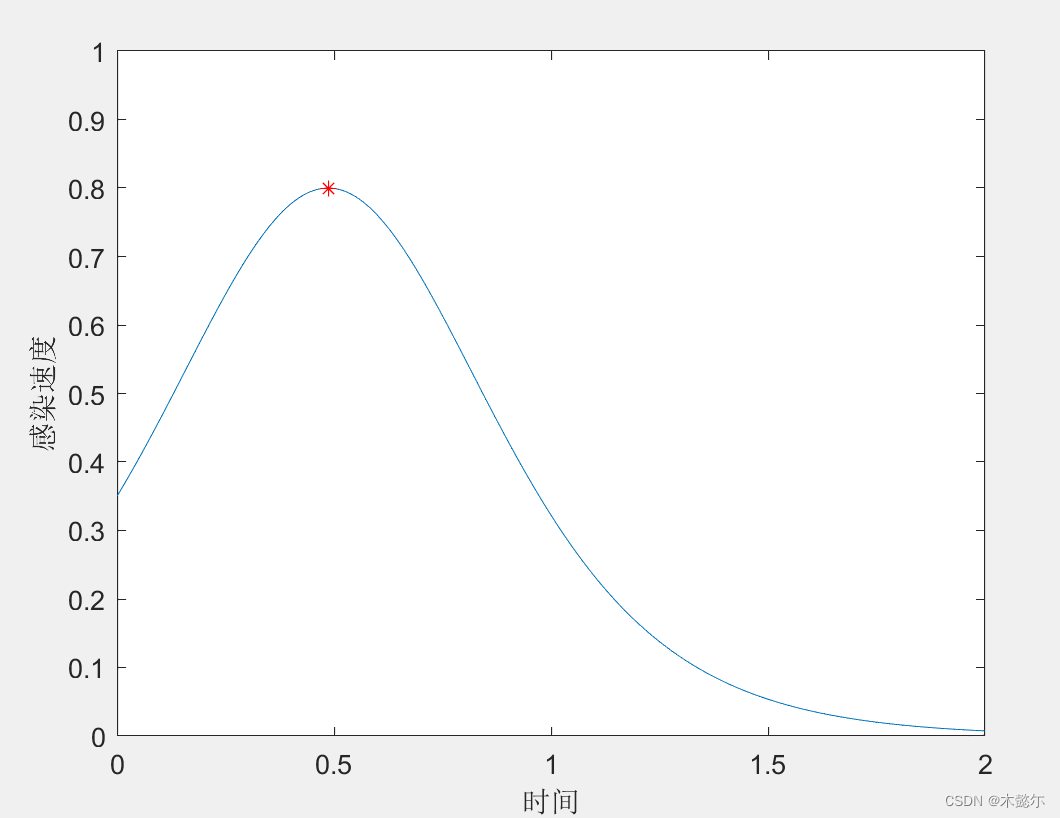
3) 若 σ≤1 则 K≤0,此时 SIS 模型右端恒为负,故曲线 I(t) 将单调下降,当 t→+∞ 时,I(t)→0 取 λ=5, I_0=0.5, σ=0.8,对应 K=−0.25,来考察传染病的传播规律:
lambda = 5;
I0 = 0.5;
sigma = 5;
xm = 1-1/sigma;
Isol(t) = subs(eval(Isol(t)), K, xm);
figure
ts = 0:0.01:2;
plot(ts, Isol(ts))
hold on
line1 = refline(0, 1);
line1.LineStyle = '--';
line = refline(0, 1-1/sigma);
line.Color = 'r';
axis([0 2 0 1.1])
xlabel('时间'), ylabel('感染比例')
σ 是一个重要参数,还是决定了感染者在总人口中的占比是持续增加,还是持续减少。
考察 σ 的定义,因为 μ 是治愈率,则 1/μ 可看作平均传染期(患者被治愈所需的平均时间)而是感染率,所以表示整个感染期内每个患者有效接触而感染的平均(健康)人数,可称为感染数。 直观理解就是,若每个患者在生病期间因有效接触而感染的人数大于 1,那么患者比例自然会增加,反之,患者比例会减少。
可推导出的一个估计式为:

根据历史数据和该公式,可以估算。
二. SIR 模型
许多传染病如天花、流感、麻疹等,治愈后就有了终生免疫力,不会再成为易感者和被感染。 传染病模型中将病愈后免疫的人,称为移出者或治愈者(Removed),考虑易感者、感染者、移出者三类人群的传染病模型,称为SIR 模型。
1. 模型建立
SIR 模型的人群转移规律如下:

t 时刻移出者占总人口的比例为 R(t),则有 S(t)+I(t)+R(t)=1,然后可以列出三类人群的变化率满足的关系:
初值条件为:I(0)=I_0, R(0)=R_0, S(0)=S_0.
注意到方程组中的第 3 个微分方程是多余方程(把第 1 个方程当多余的也可以),所以得到 SIR 模型:
初值条件为:S(0)=S_0, I(0)=I_0.
上述微分方程组是一阶非线性常微分方程组,尽管看起来简单,但是无法求出解析解,只能考虑数值解法。
2. 模型求解
(1)用 MATLAB 中的函数 ode45() 可以实现大多数微分方程(组)数值法求解
基本格式为:[t, y] = ode45(odefun, tspan, y0)
odefun 为定义微分方程(组)的关于 t 和 y 的向量值函数;
tspan 为自变量的求解范围;
y0 为初值条件向量.
返回值 t 和 y 为求解范围内一系列自变量和解函数的值对。
也可以返回一个量 sol,再配合 dveal(sol, t) 就可以计算任意t(向量)值处解函数的值。
使用 ode45() 函数的关键是,根据要求解的微分方程组把各个实参准备好,下面以 SIR 模型为例来演示。
odefun 实参
微分方程组表示为参数 odefun 所接受的标准形式,SIR 模型是一个二元微分方程组,有两个未知函数,两个微分方程,已经是标准形式:左边是未知函数的导数。要用向量 y 表示所有的未知函数(2个),则用二维列向量:y = [y(1); y(2)], 即 y(1) = S(t), y(2) = I(t).
对于标准形式的微分方程组,只需要把等号右边的各个表达式,分别作为对应的分量赋给向量 odefun 即可。
为了与模型表达式一致,这里用到“先定义含参量函数匿名函数,再对参量赋值去掉参量”的技术,这样也方便后续修改参数值。
先定义中间变量:关于 t, y, lambda, mu 的匿名函数 f,其中 lambda 和 mu 就是微分方程组中的参数,函数返回值定义为 SIR 模型右端表达式即可,注意未知函数要写成前面设定的 y 分量表示:y(1), y(2)
f = @(t, y, lambda, mu) [-lambda * y(1) * y(2); lambda * y(1) * y(2) - mu * y(2)];然后对参量赋值:
lambda = 0.6; mu = 0.3;
再代入匿名函数f:SIRfun = @(t, y) f(t, y, lambda, mu);
这样,lambda 和 mu 已经分别换成数值 0.6 和 0.3, 函数只剩关于 t 和 y, 正好作为 odefun. y0 实参
ode45() 的参数
y0 根据模型 (SIR) 的初值条件,对应地向量化赋值即可:
S0 = 0.99; I0 = 0.01; y0 = [S0; I0];
tspan 实参
自由设定 t 的求解范围:tspan = [0, 50].
(2) MATLAB 求解 SIR 模型
% y(1) = S(t), y(2) = I(t)
f = @(t,y,lambda,mu) [-lambda * y(1) * y(2);lambda * y(1) * y(2) - mu * y(2)];
lambda = 0.6;
mu = 0.3;
SIRfun = @(t,y) f(t,y,lambda,mu);
S0 = 0.99;
I0 = 0.01;
y0 = [S0; I0];
tspan = [0, 50];
[t,y] = ode45(SIRfun, tspan, y0);
R = 1 - y(:,1) - y(:,2);
sol = ode45(SIRfun, tspan, y0);
t1 = 1:0.2:2;
deval(sol, t1)
plot(t, y(:,1), t, y(:,2),'r-.', t, R, 'k.');
xlabel('t'), ylabel('y(t)')
legend('S(t)', 'I(t)', 'R(t)')

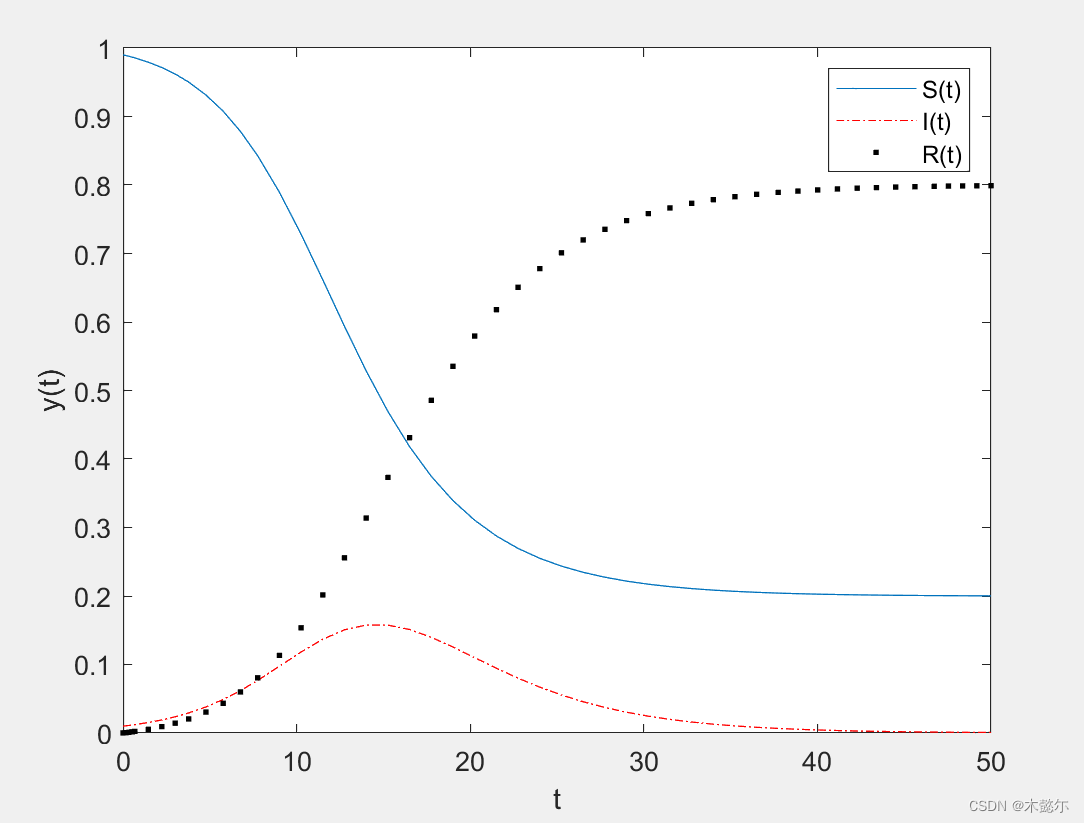
改造:换一组参数值 λ=0.5, μ=0.4, S_0=0.99, I_0=0.01. 重新求解并绘图,只需要修改代码中的参数值即可(代码略),得到图形如下:

可见,易感者比例 S(t) 单调减少,移出者比例 R(t) 单调增加,都趋向于稳定值;而感染者比例 I(t) 先增后减趋于 0 (t→∞). S(t) 趋于的稳定值表示在传染病传播过程中最终没有被感染的人数比例;最大值点和最大值表示传染病高峰(感染者最多)到来的时刻和感染者比例。这些值可以衡量传染病传播的强度和速度。
感染率 λ 和治愈率 μ(假定死亡率很低)是影响传播过程的重要参数。社会卫生水平越高感染率 λ 越小,医疗水平越高治愈率 μ 越大,于是感染数σ=λ/μ 越小,有助于控制传染病的传播。
3.进一步讨论
制绘 I(t)-S(t) 相轨线:

若 S_0>1/σ,则 I(t) 先升后降至 0,表示传染病蔓延;若 S_0<1/σ,则单调降至 0,表示传染病不会蔓延开来。
1/σ 是一个临界点,为了让传染病不蔓延,需要调整 S_0 和1/σ,具体方法:一是降低 S_0,如接种疫苗,使 S 类人群直接变成 R 类;二是提高 1/σ 使之大于 S_0,又 σ=λ/μ,也就是降低 λ 和提高 μ 如强化卫生教育和隔离病人,同时提高医疗水平。
三、舱室模型
1. 舱室模型建模方法
SIR 模型是“舱室”传染病模型的基础,可以进一步考虑更复杂的人群划分和转移,如考虑出生率、死亡率、防疫措施的作用、潜伏期、抵抗能力、考虑地域传播、考虑传播途径(接触、空气、昆虫、水源等)等。
比如,
SEIS 模型:易感-暴露-感染-不免疫
SEIR 模型:易感-暴露-感染-移出(免疫)
SIRS 模型:易感-感染-短时免疫-易感
先来讨论“舱室”传染病模型,如何从舱室转移关系图到微分方程组模型。
回顾 SIR 模型,梳理舱室转移关系图与微分方程组模型之间的对应关系(稍作修改):

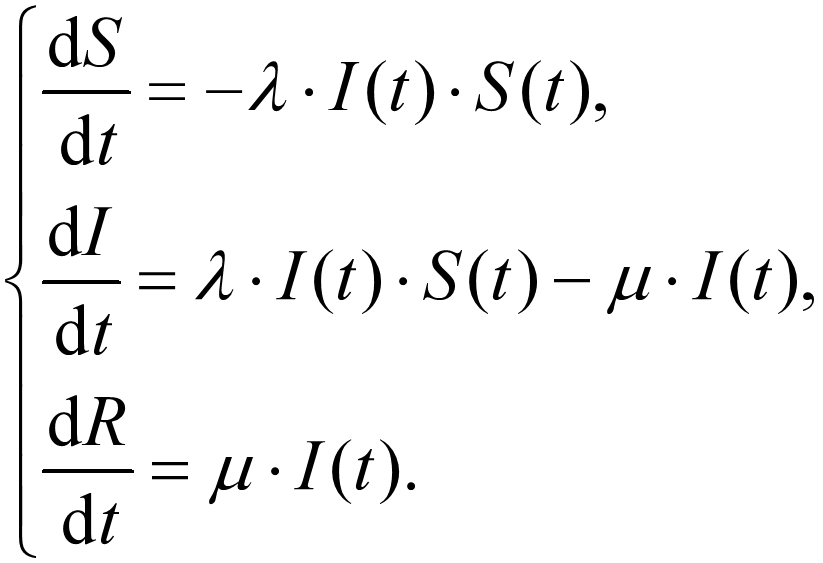
每个舱室代表一类人群(占比),对应一个未知函数,箭头及标签表示舱室之间的转移关系和转移速度;
一个舱室表示为一个微分方程,左端导数代表该类人群变化速度;
微分方程右端式子:出的箭头就是“减”,入的箭头就是“加”,都是转移速度乘以来自的舱室函数;
整体流量(流入、流出)平衡,比如1式与2式中的两个同项,2 式与 3 式中的两个同项。
注意,由于以及流量平衡关系,这样表示出来的微分方程组,有一个微分方程是多余的(可由其余微分方程表示),数值求解时需要任意去掉一个。
所以,读者可以根据具体传染病的实际情况,建立任何复杂的舱室模型,只要先绘制出舱室转移关系图,然后按上述规律表示为微分方程组,再用ode45() 进行数值求解即可。
2.SEIR模型
在 SIR 模型的基础上,将已感染但处于潜伏期人群,称为暴露者 E,也考虑进来,即构建 SEIR 模型。
SEIR 模型考虑易感者、暴露者、感染者、移出者四类人群,适合有潜伏期、治愈后获得终身免疫的传染病,如带状疱疹。
先绘制舱室转移关系图如下:

易感类 S 先以λI的速度转移到暴露类 E,再以α的速度转移到感染类 I,再以γ的速度转移到移出类 R. 再按前文的表示规律写出微分方程组:

由于 S+E+I+R=1 和流量平衡,有一个微分方程是多余的,去掉最后一个,得到 SEIR 模型:
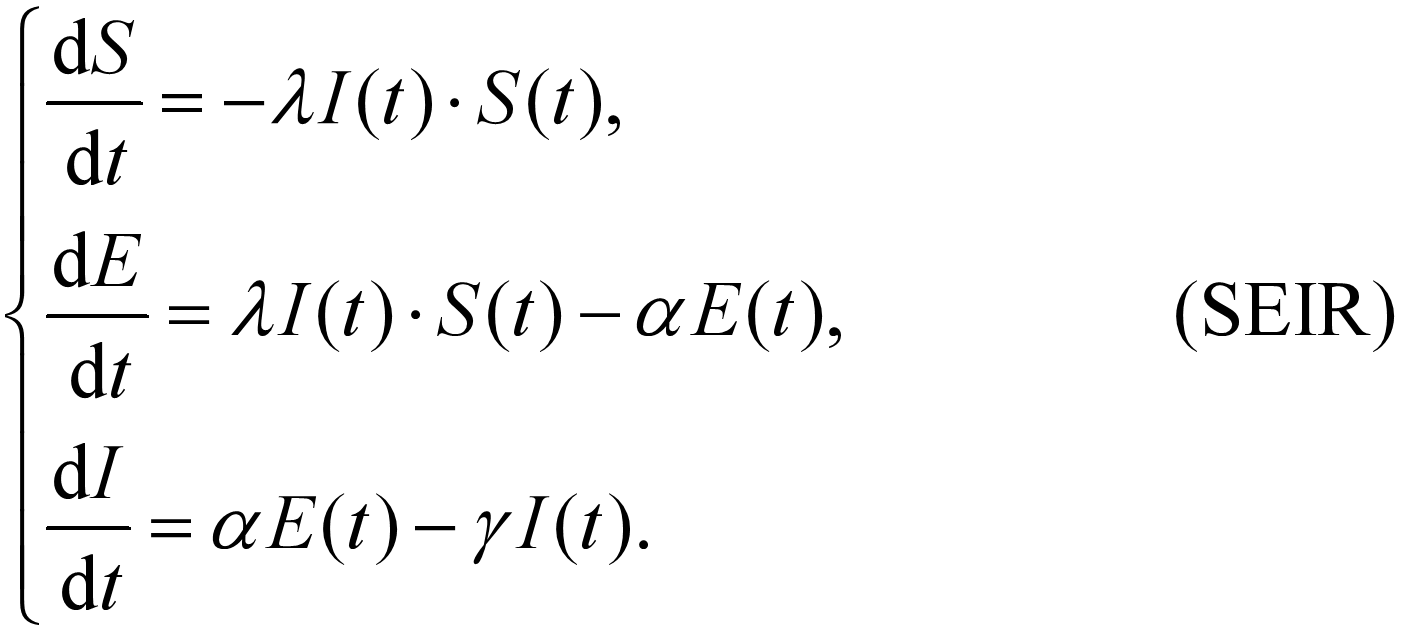
满足初值条件:S(0)=S_0, E(0)=E_0, I(0)=I_0.
(1)MATLAB求解
用上节 MATLAB 求微分方程(组)数值解的方法进行求解,代码类似:
f = @(t,y,lambda,alpha,gamma) [-lambda * y(3) * y(1);
lambda * y(3) * y(1) - alpha * y(2);
alpha * y(2) - gamma * y(3)];
lambda = 0.6;
alpha = 0.5;
gamma = 0.3;
SEIRfun = @(t,y) f(t,y,lambda,alpha,gamma);
S0 = 0.98;
E0 = 0.01;
I0 = 0.01;
y0 = [S0; E0; I0];%初值
tspan = [0, 50];
[t, y] = ode45(SEIRfun, tspan, y0);
R= 1 - y(:,1) - y(:,2) - y(:,3);%y(:,1)是S
sol = ode45(SEIRfun, tspan, y0);
t1 = 1:0.2:2;
deval(sol,t1)%t1时刻的微分方程解
deval(sol,t1,1)%计算的三个分量中的第一个分量
t2=2.5;
deval(sol,t2)
plot(t, y(:,1), t, y(:,2),'r-.', t, y(:,3), 'k.', t, R, 'g')
grid on
xlabel('t'), ylabel('y(t)')
legend('S(t)', 'E(t)', 'I(t)', 'R(t)')
以上四种模型只是传染病传播的基本模型,还有很多没有考虑的因素,如人口的出生与死亡,迁入和迁出等,还可以考虑更细致的因素, 如人群流动速度、易感人群的年龄分布、不同人群对疾病的易感性,患病者的症状轻重,人口密度,医疗卫生程度,检验检疫手段, 政府重视程度, 隔离措施、人群心理因素等。这些因素都对暴露数、发病率、治愈率、传染期长度有着直接或间接的影响。根据需要自行添加延伸即可,原理相通。
四、案例:SARS的传播规律
前文模型都是假定参数感染率和治愈率等是常数,而在实际传染病传播过程中,它们会随着预防措施的加强与医疗水平的提高而发生变化。
本节考虑 2003 年建模国赛 C 题:(北京)SARS 疫情的传播。
SARS 爆发初期,限于卫生部门和公众对其认识不足,几乎是不受制约的自然传播方式;后期随着重视和治疗手段的增强,SARS 传播受到严格控制。
SARS 治愈后具有终生免疫,同时考虑参数的时变性,采用参数时变的 SIR 模型来对北京 SARS 传播规律进行建模。
实际中对传染病的传播规律建模,就是这样一个过程:
结合传染病传播特点,划分人群并梳理转化关系,绘制转移关系图,构建 微分方程组模型;
从真实的疫情数据出发,估计出接触率、感染率、移出率等模型参数;
代入模型参数,求解微分方程组模型。
1. 时变 SIR 模型
SARS 爆发时间不长,假设期间总人数不变,用 S(t), I(t), R(t) 分别表示第 t 天易感者、感染者、移出者(治愈 + 死亡)的人数,λ(t) 和 μ(t) 分别表示第 t 天的感染率和移出率(治愈率与死亡率之和)。建立参数时变的 SIR 模型如下:

由于 S(t) 远大于 I(t) 和 R(t),且近似为常数,故可将 λ(t)S(t) 看作整体,仍记为 λ(t). 再考虑到多余方程(去掉第一个),得到
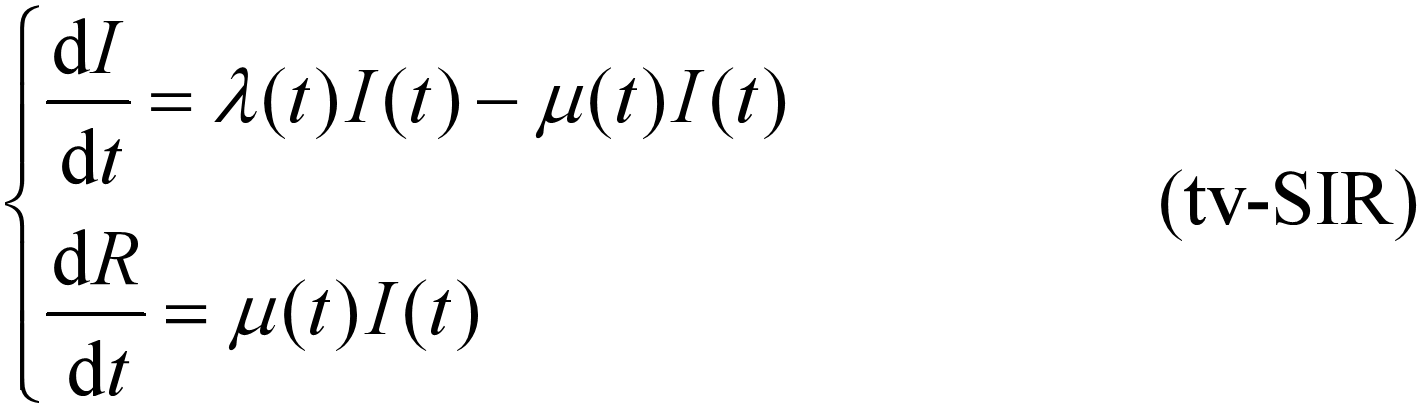 2. 模型求解
2. 模型求解
首先要确定具体参数值,即得到关于时间的参函数 λ(t), μ(t),代入模型,再数值法求解微分方程组。
参函数 λ(t), μ(t) 需要根据具体的疫情数据拟合出来。
(1) 数据整理与可视化探索
北京 SARS 疫情数据(SARSBJ.xIsx)如下表所示:
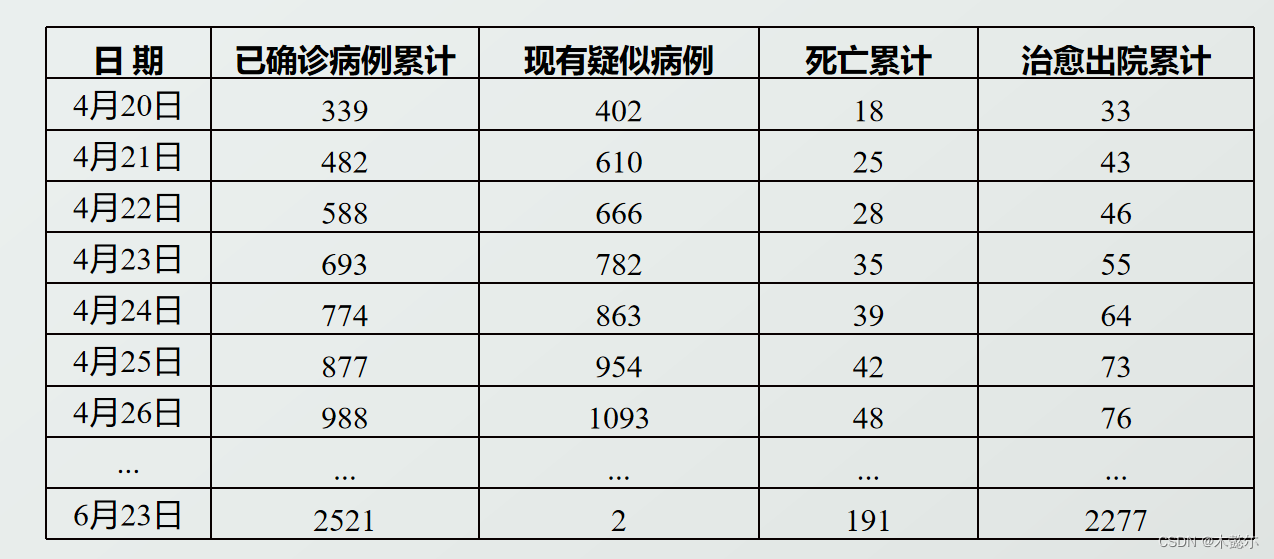
从 4 月 20 日至 6 月 23 日共 65 天,改用时间列 1: 65 表示,代表第 1 天至第 65 天。
用 MATLAB 读取数据,并计算新列:
移出列 = 死亡列 + 治愈列
感染列 = 累计确诊病例列 - 移出列