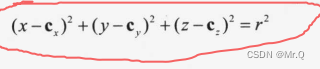目录
1 表达图元的方法
1.1 隐式表示法
1.2 参数表示
1.3 直接表示
2. 直线和射线
2.1 射线的不同表示法
2.1.1 两点表示
2.1.2 参数表示
2.1.3 相互转换
2.2 直线的不同表示法
2.2.1 隐式表示法
2.2.2 斜截式
2.2.3 相互转换
3. 球
3.1 隐式表示
1 表达图元的方法
1.1 隐式表示法
定义一个布尔函数f(x,y,z),点在图元上,则布尔函数为真,否则为假。例如
1.2 参数表示
t从0-1变化,点(x(t), y(t))的轨迹就是所描述的图元,上面描述的是中心在原点的单位圆。
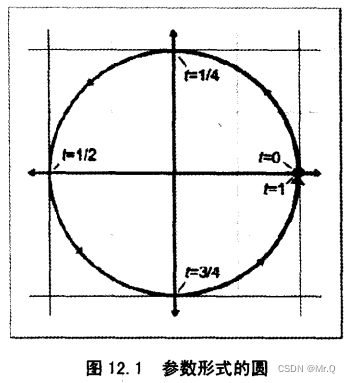
t有时的变换范围是0-L,L是图元的长度。上面的函数只有一个参数,是单变量,其轨迹是一个曲线,如果是两个变量,其轨迹是曲面。
1.3 直接表示
直接体现图元的本质信息。例如线段:两个端点表示;球:球心和半径表示。
2. 直线和射线
经典定义

书中对射线定义做了修改:有向线段。

2.1 射线的不同表示法
2.1.1 两点表示
两个端点p_org和p_end
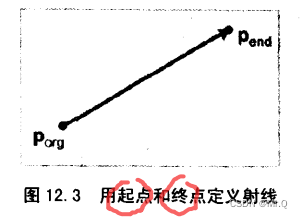
2.1.2 参数表示
或者
起点坐标是p(0)=p_0, 终点坐标是p(1)=p_0 + d,p_0 (即p_org)指定了了射线的位置信息,向量d指定了长度和方向(d = p_end - p_org = (dx, dy))。
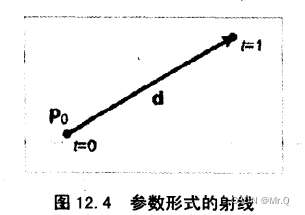
2.1.3 相互转换
两点形式 -> 参数形式
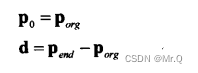
参数形式 -> 两点形式
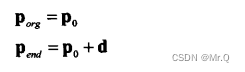
2.2 直线的不同表示法
2.2.1 隐式表示法

记向量n=[a, b], p是线上任意一点,d是标量,则向量记法的隐式表示法

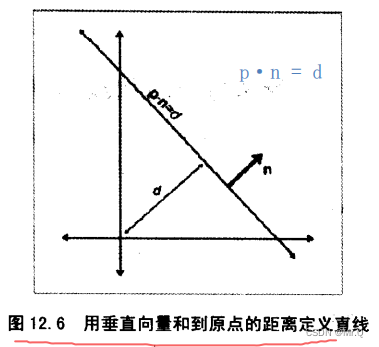
其中向量n转换成单位向量:
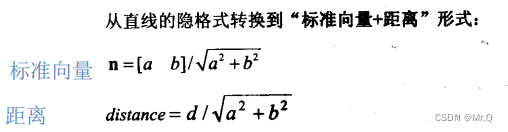
转换:射线( d = (dx, dy), p_org = (p_orgx, p_orgy) )所在的隐式表示直线
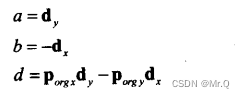
2.2.2 斜截式
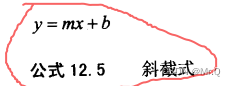

2.2.3 相互转换
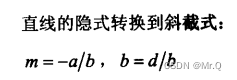
其中隐式ax+by=d, 令x=0,则截距y=d/b.
3. 球
3.1 隐式表示

到球心c的距离为给定距离r的点的集合,p为球面上点。隐式表示: