并查集

【模板】并查集

题目描述

如题，现在有一个并查集，你需要完成合并和查询操作。

输入格式

第一行包含两个整数 $N,M$ ,表示共有 $N$ 个元素和 $M$ 个操作。

接下来 $M$ 行，每行包含三个整数 $Z_i,X_i,Y_i$ 。

当 $Z_i=1$ 时，将 $X_i$ 与 $Y_i$ 所在的集合合并。

当 $Z_i=2$ 时，输出 $X_i$ 与 $Y_i$ 是否在同一集合内，是的输出
Y ；否则输出 N 。

输出格式

对于每一个 $Z_i=2$ 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N 。

样例输入 #1

4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4

样例输出 #1

N
Y
N
Y

提示

对于 $30\%$ 的数据，$N\le 10$，$M\le 20$。

对于 $70\%$ 的数据，$N\le 100$，$M\le 10^3$。

对于 $100\%$ 的数据，$1\le N\le 10^4$，$1\le M\le 2\times 10^5$，$1\le X_i,Y_i\le N$， Z i ∈ { 1 , 2 } Z_i \in \{ 1, 2 \} Zi​∈{1,2}。

以下是模板代码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 10005

int fa[MAXN]; // 用于存储每个元素所属的集合的根节点

// 查找操作，返回元素x所属集合的根节点
int find(int x) {
	if(x == fa[x]) return x; // 如果当前节点是根节点，直接返回
	return fa[x] = find(fa[x]); // 路径压缩，将x的父节点直接设为根节点，加快以后的查找
}

// 合并操作，将两个集合合并
void join(int c1, int c2) {
	int f1 = find(c1); // 查找c1所属的集合的根节点
	int f2 = find(c2); // 查找c2所属的集合的根节点
	if(f1 != f2) // 如果根节点不同，表示c1和c2不在同一集合中
		fa[f1] = f2; // 将c1的根节点的父节点设为c2的根节点，即合并两个集合
}

int main() {
	int n, m;
	cin >> n >> m; // 输入元素个数n和操作个数m
	for(int i = 1; i <= n; i++) fa[i] = i; // 初始化，每个元素初始时都是一个单独的集合，根节点就是自己
	
	while(m--) {
		int z, x, y;
		cin >> z >> x >> y; // 输入操作类型z以及两个元素x和y
		
		if(z == 1) {
			join(x, y); // 合并操作，将x和y所在的集合合并
		} else {
			if(find(x) == find(y))
				cout << "Y" << endl; // 查找操作，如果x和y在同一个集合中，输出Y
			else
				cout << "N" << endl; // 否则输出N
		}
	}
	
	return 0;
}

树状数组

树状数组1 (单点修改，区间查询)

【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 $x$

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 $x$ 个数加上 $k$

• 2 x y 含义：输出区间 $[x,y]$ 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

样例输出 #1

14
16

提示

【数据范围】

对于 $30\%$ 的数据，$1\le n\le 8$，$1\le m\le 10$；
对于 $70\%$ 的数据，$1\le n,m\le 10^4$；
对于 $100\%$ 的数据，$1\le n,m\le 5\times 10^5$。

数据保证对于任意时刻，$a$ 的任意子区间（包括长度为 $1$ 和 $n$ 的子区间）和均在 $[-2^{31},2^{31})$ 范围内。

样例说明：

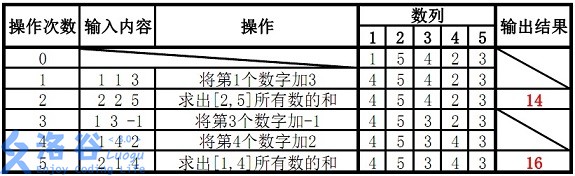
故输出结果14、16

以下是模板代码

#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
#define lowbit(x) ((x) & (-x))
int tree[N] = {0}; // 树状数组

void update(int x, int d) { // 单点修改：修改元素 a[x]，a[x] = a[x] + d
	while (x <= N) {
		tree[x] += d; // 将当前位置的值增加d
		x += lowbit(x); // 转到下一个需要修改的位置
	}
}

int sum(int x) { // 查询前缀和：返回前缀和 sum = a[1] + a[2] + ... + a[x]
	int ans = 0;
	while (x > 0) {
		ans += tree[x]; // 累加当前位置的值
		x -= lowbit(x); // 转到前一个位置
	}
	return ans;
}

int main() {
	int n, m, a;
	cin >> n >> m; // 输入数列数字个数n和操作总个数m
	for (int i = 1; i <= n; i++) {
		cin >> a; // 输入每个数列项的初始值
		update(i, a); // 初始化计算tree[]数组
	}
	while (m--) {
		int op;
		cin >> op; // 输入操作类型
		if (op == 1) {
			int x, k;
			cin >> x >> k; // 输入要修改的元素位置x和要加的值k
			update(x, k); // 对位置x的元素进行加法操作
		} else {
			int x, y;
			cin >> x >> y; // 输入查询区间[x, y]
			cout << sum(y) - sum(x - 1) << endl; // 输出区间内元素和
		}
	}
	return 0;
}

树状数组2 (单点查询，区间修改)

【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 $x$；

2. 求出某一个数的值。

输入格式

第一行包含两个整数 $N$、$M$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $N$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i $ 项的初始值。

接下来 $M$ 行每行包含 $2$ 或 $4$个整数，表示一个操作，具体如下：

操作 $1$： 格式：1 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$；

操作 $2$： 格式：2 x 含义：输出第 $x$ 个数的值。

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

样例输出 #1

6
10

提示

样例 1 解释：

故输出结果为 6、10。

---

数据规模与约定

对于 $30\%$ 的数据：$N\le 8$，$M\le 10$；

对于 $70\%$ 的数据：$N\le 10000$，$M\le 10000$；

对于 $100\%$ 的数据：$1\le N,M\le 500000$，$1\le x,y\le n$，保证任意时刻序列中任意元素的绝对值都不大于 $2^{30}$。

以下是模板代码

#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
#define lowbit(x) ((x) & (-x))
int tree[N] = {0}; // 树状数组

void update(int x, int d) { // 单点修改：修改元素 a[x]，a[x] = a[x] + d
	while (x <= N) {
		tree[x] += d; // 将当前位置的值增加d
		x += lowbit(x); // 转到下一个需要修改的位置
	}
}

int sum(int x) { // 查询前缀和：返回前缀和 sum = a[1] + a[2] + ... + a[x]
	int ans = 0;
	while (x > 0) {
		ans += tree[x]; // 累加当前位置的值
		x -= lowbit(x); // 转到前一个位置
	}
	return ans;
}

int main() {
	int n, m;
	int old = 0, a;
	cin >> n >> m; // 输入数列数字个数n和操作总个数m
	for (int i = 1; i <= n; i++) {
		cin >> a; // 输入每个数列项的初始值
		update(i, a - old); // 初始化计算tree[]数组,这里是一个差分数组
		old = a;
	}
	while (m--) {
		int op;
		cin >> op; // 输入操作类型
		if (op == 1) {
			int x, y, k;
			cin >> x >> y >> k; // 输入要修改的区间[x, y]和要加的值k
			update(x, k);
			update(y + 1, -k); // 将区间[y+1, n]的值减去k，保持区间[x, y]加上k
		} else {
			int x;
			cin >> x; // 输入要查询的位置x
			cout << sum(x) << endl; // 输出第x个数的值
		}
	}
	return 0;
}