文章目录
- Ch4. 随机变量的数字特征
- 1. 数学期望E(X)
- (1)数学期望的概念
- (2)数学期望的性质
- (3)求E(X)的三种方法
- 2. 方差D(X)
- (1)方差的定义及公式
- (2)方差的性质
- 3. 协方差Cov(X,Y)
- (1)协方差定义及公式
- (2)协方差性质
- 4. 相关系数 ρ X Y ρ_{XY} ρXY
- (1)ρ的公式
- (2)ρ的性质
- 5.独立性与不相关性
- (1)含义
- (2)判定
- 6.切比雪夫不等式
- 7.常见分布的数值特征
Ch4. 随机变量的数字特征
一维随机变量的数字特征:数学期望、方差
二维随机变量的数字特征:协方差、相关系数
1. 数学期望E(X)
(1)数学期望的概念
数学期望,又称均值
1.离散型
①一维离散型随机变量X的数学期望: E X EX EX
E X = ∑ i = 1 ∞ x i p i EX=\sum\limits_{i=1}^∞x_ip_i EX=i=1∑∞xipi
②一维离散型随机变量的函数的期望: E [ g ( X ) ] E[g(X)] E[g(X)]
E [ g ( X ) ] = ∑ i = 1 ∞ g ( x i ) p i E[g(X)]=\sum\limits_{i=1}^∞g(x_i)p_i E[g(X)]=i=1∑∞g(xi)pi
E ( X 2 ) = ∑ i = 1 ∞ x i 2 p i E(X^2)=\sum\limits_{i=1}^∞x_i^2p_i E(X2)=i=1∑∞xi2pi

③二维离散型随机变量的函数的期望: E [ g ( X , Y ) ] E[g(X,Y)] E[g(X,Y)]


例题1:16年08. 求E(XY)

分析:
| X | 0 | 1 | 2 |
|---|---|---|---|
| p p p | 4 9 \dfrac{4}{9} 94 | 4 9 \dfrac{4}{9} 94 | 1 9 \dfrac{1}{9} 91 |
| Y | 0 | 1 | 2 |
|---|---|---|---|
| p p p | 4 9 \dfrac{4}{9} 94 | 4 9 \dfrac{4}{9} 94 | 1 9 \dfrac{1}{9} 91 |
E
(
X
)
=
1
×
4
9
+
2
×
1
9
=
2
3
=
E
(
Y
)
\rm E(X)=1×\dfrac{4}{9}+2×\dfrac{1}{9}=\dfrac{2}{3}=E(Y)
E(X)=1×94+2×91=32=E(Y)
E
(
X
2
)
=
4
9
+
2
2
×
1
9
=
8
9
=
E
(
Y
2
)
\rm E(X^2)=\dfrac{4}{9}+2^2×\dfrac{1}{9}=\dfrac{8}{9}=E(Y^2)
E(X2)=94+22×91=98=E(Y2)
D
(
X
)
=
E
(
X
2
)
−
E
2
(
X
)
=
8
9
−
4
9
=
4
9
=
D
(
Y
)
\rm D(X)=E(X^2)-E^2(X)=\dfrac{8}{9}-\dfrac{4}{9}=\dfrac{4}{9}=D(Y)
D(X)=E(X2)−E2(X)=98−94=94=D(Y)
难点、易错点在求E(XY)
P{XY=4}=P{X=2,Y=2}=0
P{XY=2}=P{X=2,Y=1}+P{X=1,Y=2}=0
P{XY=1}=P{X=1,Y=1}=
2
×
1
3
×
1
3
=
2
9
2×\dfrac{1}{3}×\dfrac{1}{3}=\dfrac{2}{9}
2×31×31=92
P{XY=0}=
1
−
2
9
=
7
9
1-\dfrac{2}{9}=\dfrac{7}{9}
1−92=97
| XY | 0 | 1 | 2 | 4 |
|---|---|---|---|---|
| p p p | 7 9 \dfrac{7}{9} 97 | 2 9 \dfrac{2}{9} 92 | 0 | 0 |
∴ E ( X Y ) = 2 9 E(XY)=\dfrac{2}{9} E(XY)=92
ρ X Y = C o v ( X Y ) D ( X ) D ( Y ) = E ( X Y ) − E ( X ) ⋅ E ( Y ) D ( X ) ⋅ D ( Y ) = 2 9 − 4 9 4 9 = − 1 2 \rm ρ_{XY}=\dfrac{Cov(XY)}{\sqrt{D(X)D(Y)}}=\dfrac{E(XY)-E(X)·E(Y)}{\sqrt{D(X)·D(Y)}}=\dfrac{\dfrac{2}{9}-\dfrac{4}{9}}{\dfrac{4}{9}}=-\dfrac{1}{2} ρXY=D(X)D(Y)Cov(XY)=D(X)⋅D(Y)E(XY)−E(X)⋅E(Y)=9492−94=−21
答案:A
2.连续型
①一维连续型随机变量X的数学期望: E X EX EX
E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x E(X)=\int_{-∞}^{+∞}xf(x)dx E(X)=∫−∞+∞xf(x)dx
②一维连续型随机变量的函数的数学期望: E [ g ( X ) ] E[g(X)] E[g(X)]
E ( Y ) = E [ g ( X ) ] = ∫ − ∞ + ∞ g ( x ) f ( x ) d x E(Y)=E[g(X)]=\int_{-∞}^{+∞}g(x)f(x)\rm dx E(Y)=E[g(X)]=∫−∞+∞g(x)f(x)dx

E ( X 2 ) = ∫ − ∞ + ∞ x 2 f ( x ) d x E(X^2)=\int_{-∞}^{+∞}x^2f(x)dx E(X2)=∫−∞+∞x2f(x)dx
③二维连续型随机变量的函数的数学期望: E [ g ( X , Y ) ] E[g(X,Y)] E[g(X,Y)]
(X,Y)为连续型随机变量,概率密度为f(x,y),且 ∫ − ∞ + ∞ g ( x , y ) f ( x , y ) d x d y \int_{-∞}^{+∞}g(x,y)f(x,y)dxdy ∫−∞+∞g(x,y)f(x,y)dxdy绝对收敛,
则(X,Y)的数学期望为: E [ g ( X , Y ) ] = ∫ − ∞ + ∞ g ( x , y ) f ( x , y ) d x d y E[g(X,Y)]=\int_{-∞}^{+∞}g(x,y)f(x,y)dxdy E[g(X,Y)]=∫−∞+∞g(x,y)f(x,y)dxdy
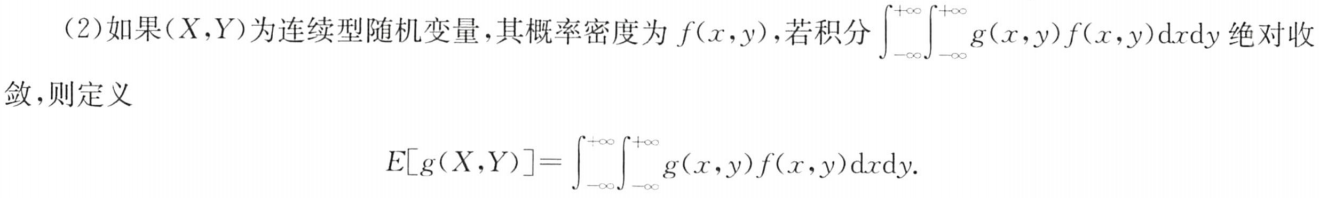
(2)数学期望的性质
1.线性性质:
①
E
C
=
C
EC=C
EC=C
②
E
(
a
X
+
C
)
=
a
E
X
+
C
E(aX+C)=aEX+C
E(aX+C)=aEX+C
③
E
(
X
±
Y
)
=
E
X
±
E
Y
E(X±Y)=EX±EY
E(X±Y)=EX±EY
2.若X,Y独立,则:
①
E
(
X
Y
)
=
E
X
⋅
E
Y
E(XY)=EX·EY
E(XY)=EX⋅EY
②
E
[
f
(
X
)
g
(
Y
)
]
=
E
[
f
(
X
)
]
⋅
E
[
g
(
Y
)
]
E[f(X)g(Y)]=E[f(X)]·E[g(Y)]
E[f(X)g(Y)]=E[f(X)]⋅E[g(Y)]
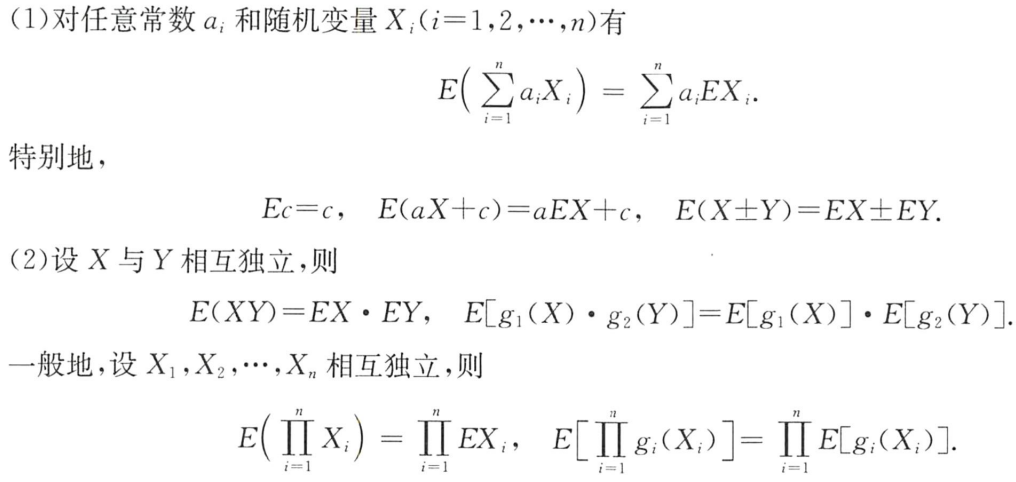
例题1:20年14.

分析:只要随机变量相同,其函数的概率密度仍不变。求E(XsinX)时的概率密度仍为f(x)
E
(
X
)
=
∫
−
∞
+
∞
x
f
(
x
)
d
x
E(X)=\int_{-∞}^{+∞}xf(x)dx
E(X)=∫−∞+∞xf(x)dx
E
[
g
(
X
)
]
=
∫
−
∞
+
∞
g
(
x
)
f
(
x
)
d
x
E[g(X)]=\int_{-∞}^{+∞}g(x)f(x)\rm dx
E[g(X)]=∫−∞+∞g(x)f(x)dx
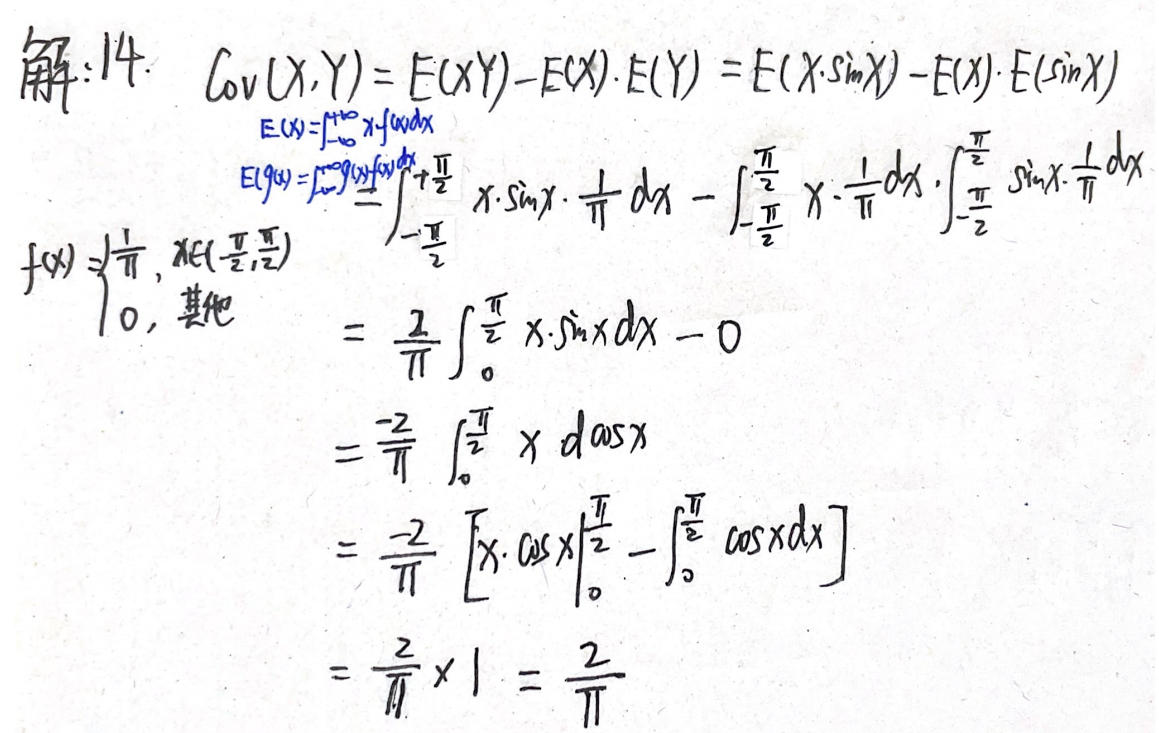
答案: 2 π \dfrac{2}{π} π2
例题2:18年23(2)
(3)求E(X)的三种方法
①先用EX的性质,化简目标数学期望:
如
E
(
X
+
Y
)
=
E
X
+
E
Y
E(X+Y)=EX+EY
E(X+Y)=EX+EY
②特殊分布的数字特征:
X是否满足某一特殊分布,若满足,根据其数字特征直接得出EX
③定义法:
若上述两项都不能再使用后,别无选择只能用定义。如连续型随机变量的数学期望为
E
(
X
)
=
∫
−
∞
+
∞
x
f
(
x
)
d
x
E(X)=\int_{-∞}^{+∞}xf(x)dx
E(X)=∫−∞+∞xf(x)dx
例题1:24基础30讲 4.9

分析:
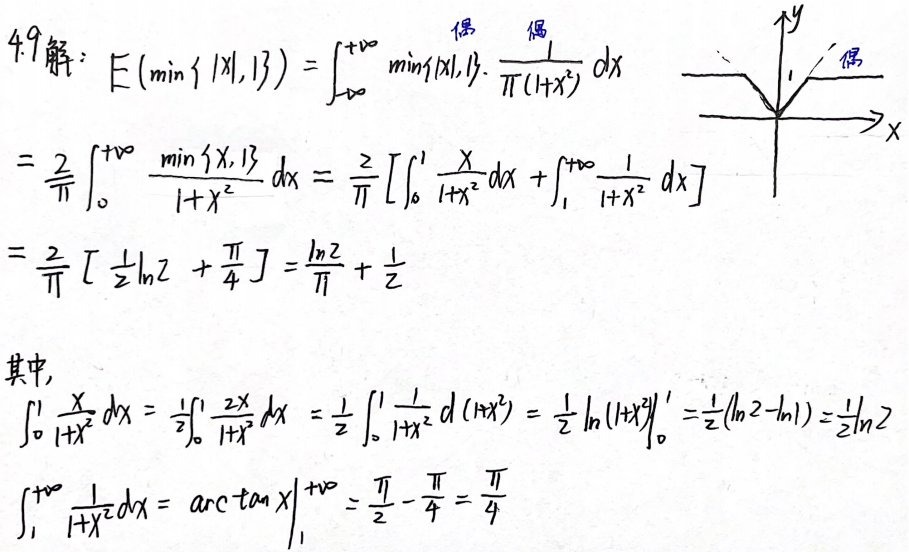
答案:
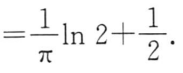
2. 方差D(X)
(1)方差的定义及公式
D ( X ) = E [ ( X − E X ) 2 ] = E ( X 2 ) − E 2 ( X ) D(X)=E[(X-EX)^2]=E(X^2)- E^2(X) D(X)=E[(X−EX)2]=E(X2)−E2(X)
E ( X 2 ) = D ( X ) + E 2 ( X ) E(X²)=D(X)+E²(X) E(X2)=D(X)+E2(X)

(2)方差的性质
①
D
C
=
0
DC=0
DC=0
②
D
(
C
X
)
=
C
2
D
X
D(CX)=C²DX
D(CX)=C2DX
③
D
(
a
X
+
C
)
=
a
2
D
X
D(aX+C)=a^2DX
D(aX+C)=a2DX
④
D
(
X
±
Y
)
=
D
X
+
D
Y
±
2
C
o
v
(
X
,
Y
)
D(X±Y)=DX+DY±2{\rm Cov}(X,Y)
D(X±Y)=DX+DY±2Cov(X,Y)
⑤
D
(
a
X
±
b
Y
)
=
a
2
D
X
+
b
2
D
Y
±
2
a
b
C
o
v
(
X
,
Y
)
D(aX±bY)=a²DX+b²DY±2ab{\rm Cov}(X,Y)
D(aX±bY)=a2DX+b2DY±2abCov(X,Y) 若X与Y独立,则Cov(X,Y)=0
⑥
C
o
v
(
X
,
X
)
=
D
(
X
)
{\rm Cov}(X,X)=D(X)
Cov(X,X)=D(X)
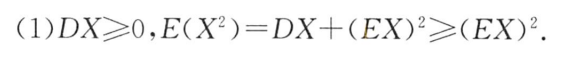
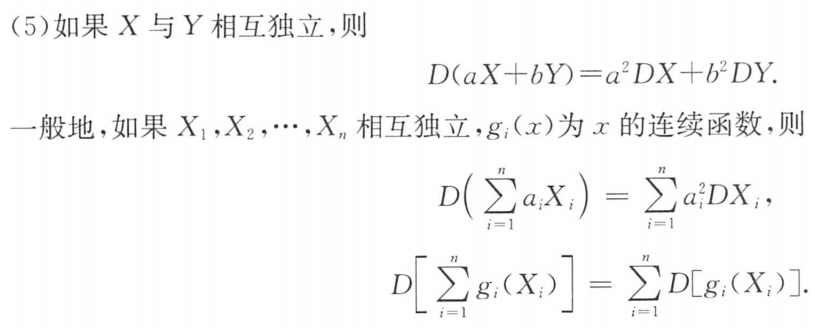
例题1:22年8. 方差的性质
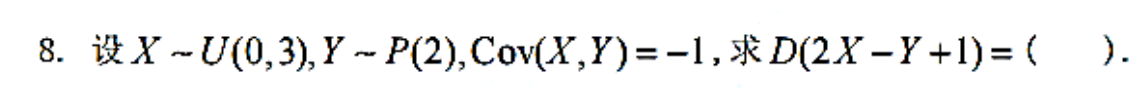
分析:注意,X与Y没说独立就是不独立,不要误选了5
X~U(0,3),D(X)=
(
3
−
0
)
2
12
=
3
4
\frac{(3-0)²}{12}=\frac{3}{4}
12(3−0)2=43
Y~P(2),D(Y)=2
D(2X-Y+1)=D(2X-Y)=4D(X)+D(Y)-4Cov(X,Y)=
4
×
3
4
+
2
−
4
×
(
−
1
)
4×\frac{3}{4}+2-4×(-1)
4×43+2−4×(−1)=3+2+4=9
答案:9
例题2:11年14.
E
(
X
2
)
=
D
(
X
)
+
E
2
(
X
)
\rm E(X²)=D(X)+E²(X)
E(X2)=D(X)+E2(X)
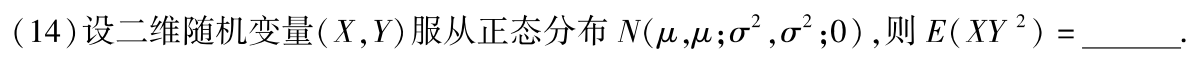
分析:
∵ρ=0,∴X与Y不相关 又∵(X,Y)服从正态分布,∴X与Y独立
E
(
X
Y
2
)
=
X
与
Y
独立
E
(
X
)
⋅
E
(
Y
2
)
=
E
(
X
)
⋅
[
D
(
Y
)
+
E
2
(
Y
)
]
=
μ
(
σ
2
+
μ
2
)
\rm E(XY²)\xlongequal[]{X与Y独立}E(X)·E(Y²)=E(X)·[D(Y)+E²(Y)]=μ(σ²+μ²)
E(XY2)X与Y独立E(X)⋅E(Y2)=E(X)⋅[D(Y)+E2(Y)]=μ(σ2+μ2)
答案:μ(σ²+μ²)
例题3:18年23(2)
3. 协方差Cov(X,Y)
(1)协方差定义及公式
C o v ( X , Y ) = E [ ( X − E X ) ( Y − E Y ) ] = E ( X Y ) − E ( X ) ⋅ E ( Y ) {\rm Cov}(X,Y) =E[(X-EX)(Y-EY)]={\rm E}(XY)-{\rm E}(X)·{\rm E}(Y) Cov(X,Y)=E[(X−EX)(Y−EY)]=E(XY)−E(X)⋅E(Y)
计算Cov(X,Y)=EXY-EX·EY时,简化计算:
①若有EX=0则EY不用算了,若有EY=0则EX不用算了。
②若E(XY)用定义发现是奇函数,则在对称区间上积分为0
(2)协方差性质
1.对称性
①
C
o
v
(
X
,
Y
)
=
C
o
v
(
Y
,
X
)
{\rm Cov}(X,Y)={\rm Cov}(Y,X)
Cov(X,Y)=Cov(Y,X) 【
ρ
X
Y
=
ρ
Y
X
ρ_{XY}=ρ_{YX}
ρXY=ρYX】
②
C
o
v
(
X
,
X
)
=
D
(
X
)
{\rm Cov}(X,X) ={\rm D}(X)
Cov(X,X)=D(X) 【
ρ
X
X
=
1
ρ_{XX}=1
ρXX=1】
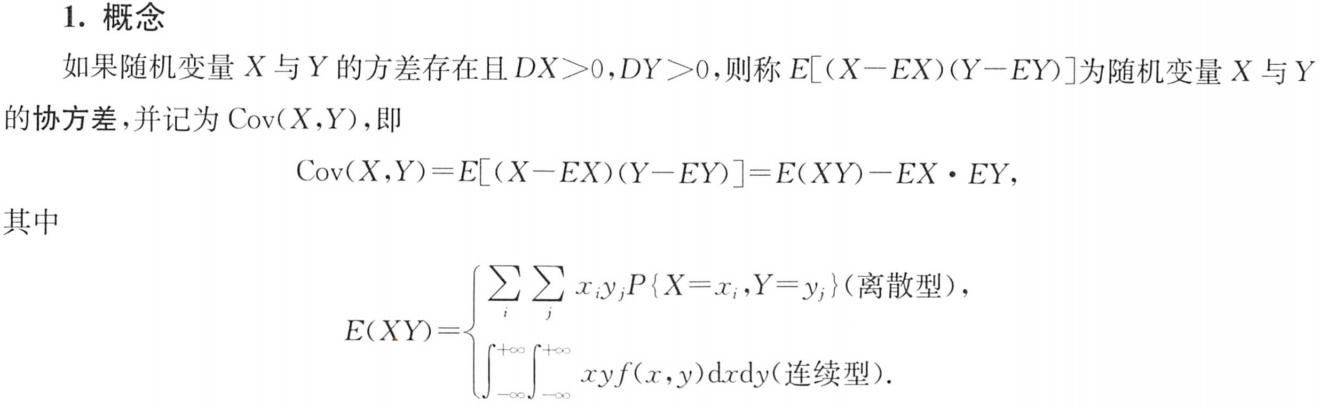
2.线性性质:
①
C
o
v
(
X
,
C
)
=
0
{\rm Cov}(X,C)=0
Cov(X,C)=0
②
C
o
v
(
X
1
+
X
2
,
Y
)
=
C
o
v
(
X
1
,
Y
)
+
C
o
v
(
X
2
,
Y
)
{\rm Cov}(X₁+X₂,Y) ={\rm Cov}(X₁,Y) +{\rm Cov}(X₂,Y)
Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
③
C
o
v
(
a
X
+
c
,
b
Y
+
d
)
=
a
b
C
o
v
(
X
,
Y
)
{\rm Cov}(aX+c,bY+d) =ab\ {\rm Cov}(X,Y)
Cov(aX+c,bY+d)=ab Cov(X,Y)
④若X与Y独立,则Cov(X,Y)=0
1.②证明: C o v ( X , X ) = E ( X ⋅ X ) − E X ⋅ E X = E ( X 2 ) − E 2 ( X ) = D ( X ) {\rm Cov}(X,X) = E(X·X)-EX·EX=E(X^2)-E^2(X)={\rm D}(X) Cov(X,X)=E(X⋅X)−EX⋅EX=E(X2)−E2(X)=D(X)
2.性质应用举例: C o v ( X , − X + n ) = C o v ( X , − X ) + C o v ( X , n ) = − C o v ( X , X ) + 0 = − D ( x ) {\rm Cov}(X,-X+n)={\rm Cov}(X,-X)+{\rm Cov}(X,n)=-{\rm Cov}(X,X)+0=-D(x) Cov(X,−X+n)=Cov(X,−X)+Cov(X,n)=−Cov(X,X)+0=−D(x)
例题1:23李林六套卷(一) 9.

分析:用协方差的性质求Cov
求Cov
①协方差的定义(公式):Cov(XY)=E(XY)-E(X)E(Y)
②协方差的性质

答案:A
例题2:01年10.

分析: X + Y = n , ∴ Y = − X + n X+Y=n,∴Y=-X+n X+Y=n,∴Y=−X+n
① ρ X Y = C o v ( X , Y ) D ( X ) D ( Y ) = C o v ( X , − X + n ) D ( X ) D ( − X + n ) = − D ( X ) D ( X ) ρ_{XY}=\dfrac{Cov(X,Y)}{\sqrt{D(X)D(Y)}}=\dfrac{Cov(X,-X+n)}{\sqrt{D(X)D(-X+n)}}=\dfrac{-D(X)}{D(X)} ρXY=D(X)D(Y)Cov(X,Y)=D(X)D(−X+n)Cov(X,−X+n)=D(X)−D(X)
② P { Y = − X + n } = 1 , a = − 1 < 0 P\{Y=-X+n\}=1,a=-1<0 P{Y=−X+n}=1,a=−1<0,∴负相关, ρ X Y = − 1 ρ_{XY}=-1 ρXY=−1
答案:A
4. 相关系数 ρ X Y ρ_{XY} ρXY
(1)ρ的公式
ρ = C o v ( X , Y ) D X D Y ρ=\dfrac{Cov(X,Y)}{\sqrt{DX}\sqrt{DY}} ρ=DXDYCov(X,Y)称为随机变量X与Y的相关系数。
ρ
X
Y
=
0
ρ_{XY}=0
ρXY=0称为X与Y不相关,即 无线性相关。
ρ
X
Y
≠
0
ρ_{XY}≠0
ρXY=0则称为X与Y相关。即 有线性相依性。
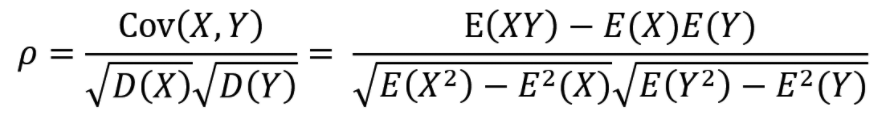
(2)ρ的性质
1.对称性:
①
ρ
X
Y
=
ρ
Y
X
ρ_{XY}=ρ_{YX}
ρXY=ρYX
②
ρ
X
X
=
1
ρ_{XX}=1
ρXX=1
2.有界性:
−
1
≤
ρ
X
Y
≤
1
-1≤ρ_{XY}≤1
−1≤ρXY≤1
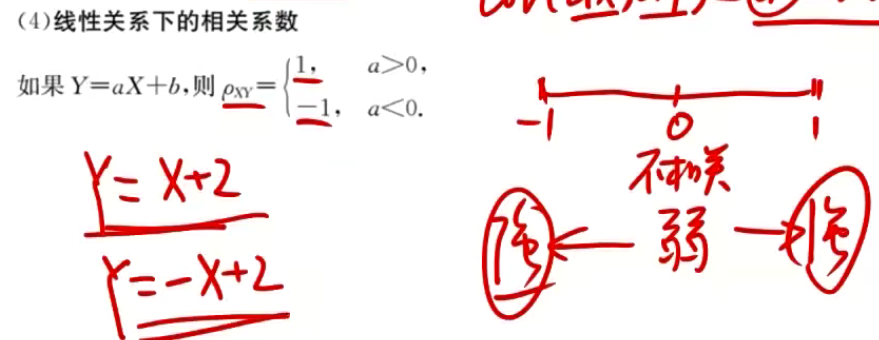
3.正相关、负相关、不相关
①正相关:
P
{
Y
=
a
X
+
b
}
=
1
P\{Y=aX+b\}=1
P{Y=aX+b}=1。
a
>
0
时
ρ
=
1
a>0时ρ=1
a>0时ρ=1
②负相关:
P
{
Y
=
a
X
+
b
}
=
−
1
P\{Y=aX+b\}=-1
P{Y=aX+b}=−1。
a
<
0
时
ρ
=
−
1
a<0时ρ=-1
a<0时ρ=−1
③不相关:
P
{
Y
=
a
X
+
b
}
=
0
P\{Y=aX+b\}=0
P{Y=aX+b}=0
例题1:16年8.

答案:A
例题2:01年10.
5.独立性与不相关性
(1)含义
| 独立/相关 | 含义 |
|---|---|
| 不独立 | 有任意函数关系 |
| 独立 | 无任何函数关系 |
| 相关 | 有线性函数关系 |
| 不相关 | ρXY= 0,X与Y无线性函数关系,但有可能有其他非线性函数关系 |
①独立,一定不相关:没有任何函数关系,自然也没有线性函数关系
②相关,一定不独立:有线性函数关系,算是X与Y有一种函数关系了,不独立。
③不相关,不一定独立:没有线性函数关系,但可能有非线性函数关系
注:仅当(X,Y)服从二维正态分布时,独立与不相关是等价的。其他时候,独立是不相关的充分条件。
(2)判定
1.相关性:用数字特征判定相关性 (5个不相关的等价条件)
\quad
①X与Y不相关
⇔
\Leftrightarrow
⇔ ②
ρ
X
Y
=
0
ρ_{XY}=0
ρXY=0
⇔
\Leftrightarrow
⇔ ③
C
o
v
(
X
,
Y
)
=
0
Cov(X,Y)=0
Cov(X,Y)=0
⇔
\Leftrightarrow
⇔ ④
E
(
X
Y
)
=
E
X
⋅
E
Y
E(XY)=EX·EY
E(XY)=EX⋅EY
⇔
\Leftrightarrow
⇔ ⑤
D
(
X
±
Y
)
=
D
X
+
D
Y
D(X±Y)=DX+DY
D(X±Y)=DX+DY
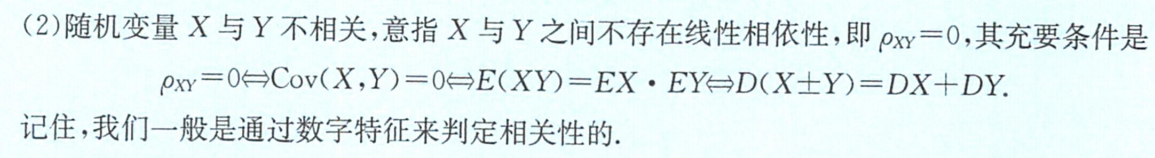
2.独立性:用分布判断独立性,构造事件
\quad
①X与Y不独立
⇔
\Leftrightarrow
⇔ ②
P
{
X
≤
a
,
Y
≤
a
}
≠
P
{
X
≤
a
}
⋅
P
{
Y
≤
a
}
P\{X≤a,Y≤a\}≠P\{X≤a\}·P\{Y≤a\}
P{X≤a,Y≤a}=P{X≤a}⋅P{Y≤a}
⇔
\Leftrightarrow
⇔ ③
ョ
x
0
,
y
0
ョx_0,y_0
ョx0,y0使得
F
(
x
0
,
y
0
)
≠
F
X
(
x
0
)
⋅
F
Y
(
y
0
)
F(x_0,y_0)≠F_X(x_0)·F_Y(y_0)
F(x0,y0)=FX(x0)⋅FY(y0)
联合分布≠边缘分布的乘积

3.判断顺序:
先判断相关性(Cov(x,y)),再判断独立性(看分布)

相关性与独立性的关系,详解见此篇
6.切比雪夫不等式
①距离均值偏差较大的概率是很小的:
P
{
∣
X
−
E
(
X
)
∣
≥
ε
}
≤
D
(
X
)
ε
2
P\{|X-E(X)|≥ε\}≤\dfrac{D(X)}{ε^2}
P{∣X−E(X)∣≥ε}≤ε2D(X)
②距离均值偏差较小的概率是比较大的:
P
{
∣
X
−
E
(
X
)
∣
<
ε
}
≥
1
−
D
(
X
)
ε
2
P\{|X-E(X)|<ε\}≥1-\dfrac{D(X)}{ε^2}
P{∣X−E(X)∣<ε}≥1−ε2D(X)
①切比雪夫不等式描述的是随机变量X偏离均值一定范围的概率,给的是一个保守的概率。
例如:正态分布 X~N(μ,σ²), P { ∣ X − μ ∣ < 2 σ } ≥ 1 − σ 2 4 σ 2 = 75 % P\{|X-μ|<2σ\}≥1-\dfrac{σ^2}{4σ^2}=75\% P{∣X−μ∣<2σ}≥1−4σ2σ2=75%,而实际上2σ区间内的概率应为95%
②切比雪夫不等式需要求三个值:E(X)、D(X)、ε。由 ∣ X − E ( X ) ∣ |X-E(X)| ∣X−E(X)∣得出ε大小
例题1:01年5. 切比雪夫不等式

分析:
由切比雪夫不等式,
P
{
∣
X
−
E
(
X
)
∣
≥
ε
}
≤
D
(
X
)
ε
2
P\{|X-E(X)|≥ε\}≤\dfrac{D(X)}{ε²}
P{∣X−E(X)∣≥ε}≤ε2D(X),得此题
ε
=
2
,
D
(
X
)
=
2
ε=2,D(X)=2
ε=2,D(X)=2
代入得
P
{
∣
X
−
E
(
X
)
∣
≥
2
}
≤
2
2
2
=
1
2
P\{|X-E(X)|≥2\}≤\dfrac{2}{2²}=\dfrac{1}{2}
P{∣X−E(X)∣≥2}≤222=21
答案: 1 2 \dfrac{1}{2} 21
例题2:24基础30讲 4.15

分析:
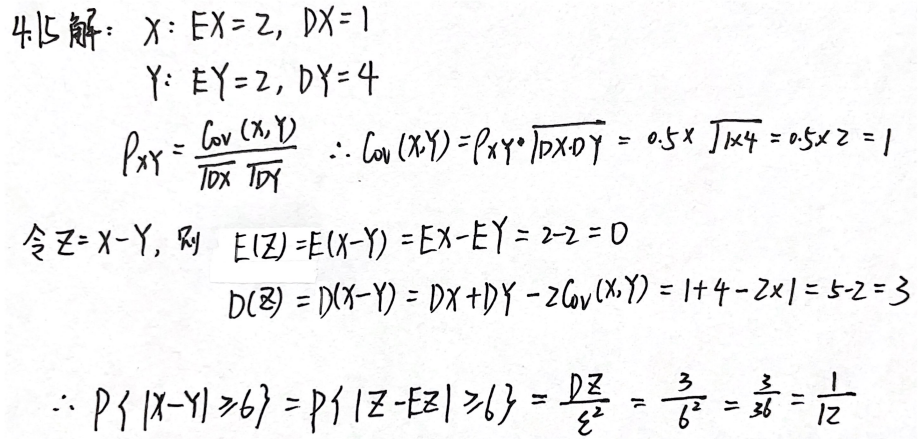
答案: 1 12 \dfrac{1}{12} 121
习题2:23李林六套卷(五)16.
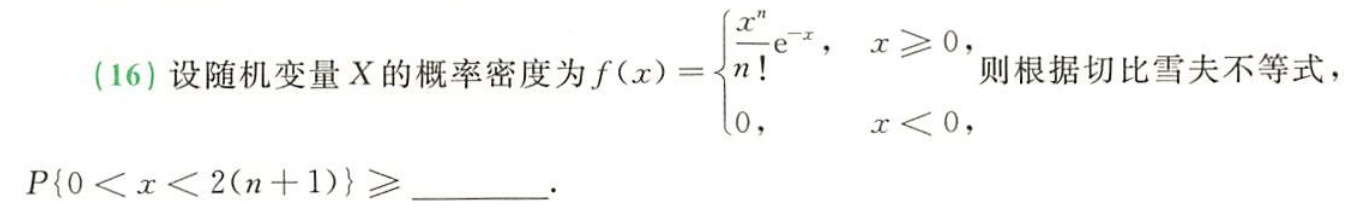
分析:切比雪夫不等式需要求三个值:E(X)、D(X)、ε
由
∣
X
−
E
(
X
)
∣
|X-E(X)|
∣X−E(X)∣得出ε大小。

答案: n n + 1 \dfrac{n}{n+1} n+1n
7.常见分布的数值特征
| 分布 | 分布律或概率密度 | 数学期望E(X) | 方差D(X) |
|---|---|---|---|
| 0-1分布 | P { X = k } = p k ( 1 − p ) 1 − k , k = 0 , 1 P\{X=k\}=p^k(1-p)^{1-k},k=0,1 P{X=k}=pk(1−p)1−k,k=0,1 | p p p | p ( 1 − p ) p(1-p) p(1−p) |
| 二项分布 B ( n , p ) B(n,p) B(n,p) | P { X = k } = C n k p k ( 1 − p ) n − k P\{X=k\}={\rm C}_n^kp^k(1-p)^{n-k} P{X=k}=Cnkpk(1−p)n−k, k = 0 , 1 , 2 , . . . , n k=0,1,2,...,n k=0,1,2,...,n | n p np np | n p ( 1 − p ) np(1-p) np(1−p) |
| 泊松分布 P ( λ ) P(λ) P(λ) | P { X = k } = λ k k ! e − λ P\{X=k\} = \dfrac{λ^k}{k!}e^{-λ} P{X=k}=k!λke−λ, k = 0 , 1 , 2 , . . . k=0,1,2,... k=0,1,2,... | λ λ λ | λ λ λ |
| 几何分布 G ( p ) G(p) G(p) | P { X = k } = ( 1 − p ) k − 1 p P\{X=k\}=(1-p)^{k-1}p P{X=k}=(1−p)k−1p, k = 1 , 2 , . . . k=1,2,... k=1,2,... | 1 p \dfrac{1}{p} p1 | 1 − p p 2 \dfrac{1-p}{p^2} p21−p |
| 均匀分布 U ( a , b ) U(a,b) U(a,b) | f ( x ) = { 1 b − a , a < x < b 0 , 其他 f(x)=\begin{cases} \dfrac{1}{b-a}, & a<x<b\\ 0 , & 其他 \end{cases} f(x)=⎩ ⎨ ⎧b−a1,0,a<x<b其他 | a + b 2 \dfrac{a+b}{2} 2a+b | ( b − a ) 2 12 \dfrac{(b-a)^2}{12} 12(b−a)2 |
| 指数分布 E ( λ ) E(λ) E(λ) | f ( x ) = { λ e − λ x , x > 0 0 , x ≤ 0 f(x)=\begin{cases} λe^{-λx}, & x>0\\ 0, & x≤0 \end{cases} f(x)={λe−λx,0,x>0x≤0 | 1 λ \dfrac{1}{λ} λ1 | 1 λ 2 \dfrac{1}{λ^2} λ21 |
| 正态分布 N ( μ , σ 2 ) N(μ,σ^2) N(μ,σ2) | f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 ( − ∞ < x < + ∞ ) f(x)=\dfrac{1}{\sqrt{2π}σ}e^{-\frac{{(x-μ^)}^2}{2σ^2}} \quad(-∞<x<+∞) f(x)=2πσ1e−2σ2(x−μ)2(−∞<x<+∞) | μ μ μ | σ 2 σ^2 σ2 |
| 卡方分布 χ 2 χ^2 χ2 | E ( χ 2 ) = n E(χ^2)=n E(χ2)=n | D ( χ 2 ) = 2 n D(χ^2)=2n D(χ2)=2n |
例题1:24基础30讲 4.8

分析:
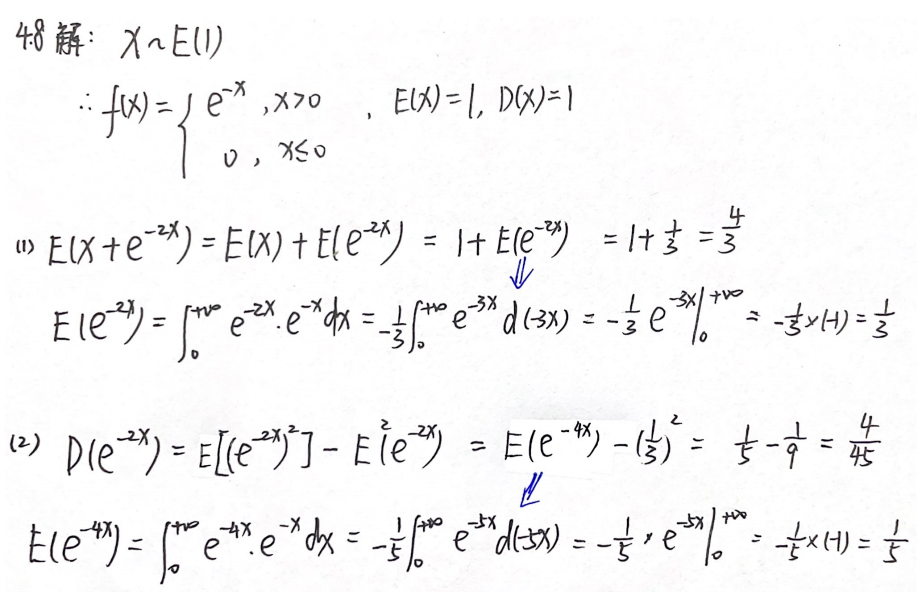
答案: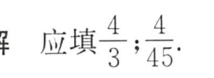
例题2:11年23.(2) 卡方分布

分析:估计量服从卡方分布,用卡方分布的数字特征来求估计量的期望与方差