在微分方程中,常见的形式是:
x
′
=
f
(
x
,
t
)
x'=f(x,t)
x′=f(x,t)
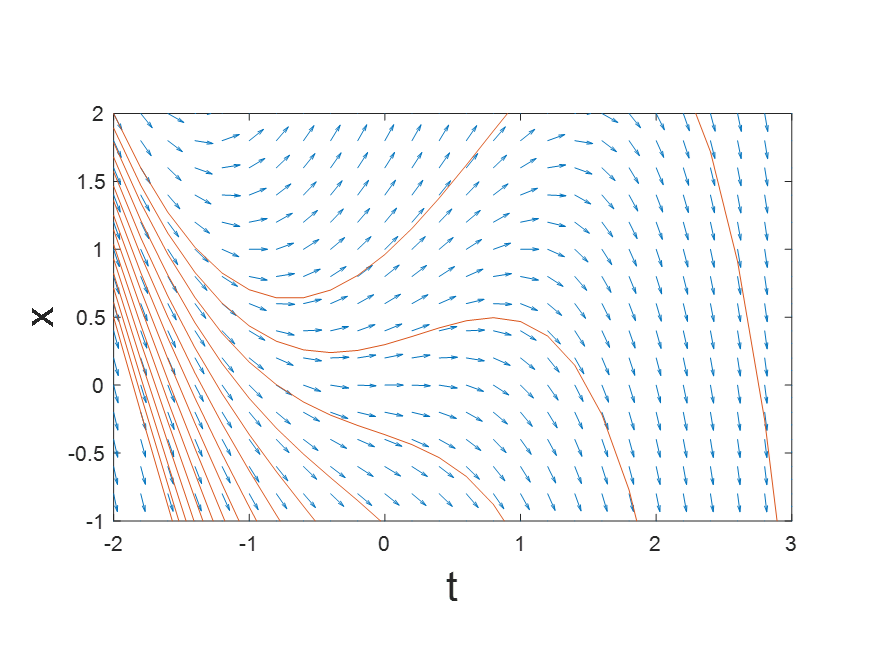
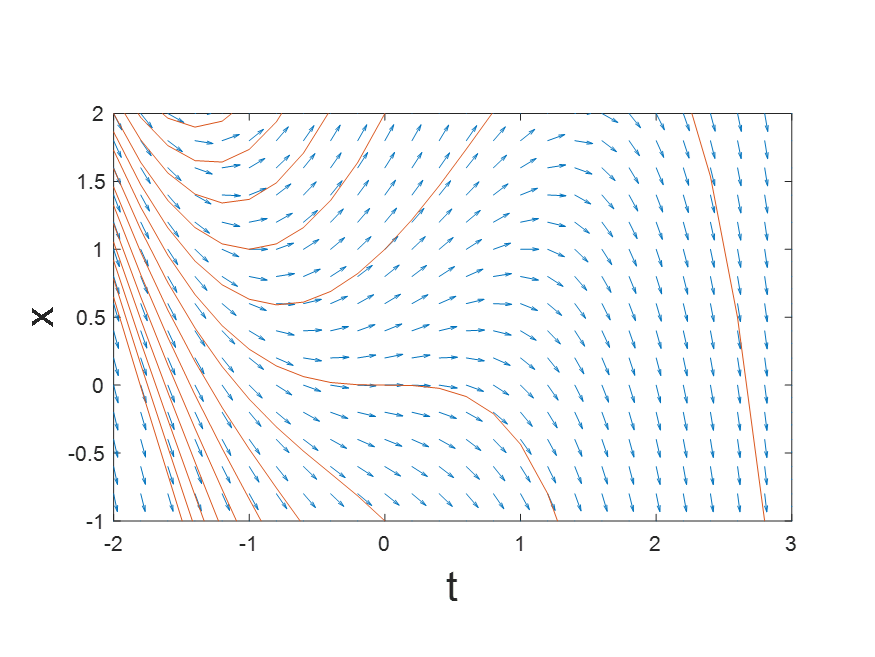
方向场的每一个矢量可以形象地刻画一阶微分方程的解。在方向场中的每个点处,都会出现一条其斜率等于通过该点的微分方程解的矢量。给定一个初值,微分方程对应一条curve曲线,点上的方向矢量和相切。
例子:解析解
d x d t = x − t 2 \frac{d x}{d t}=x-t^{2} dtdx=x−t2
我们可以求得解析解:
x ( t ) = C e t + t 2 + 2 t + 2 x(t)=C e^{t}+t^{2}+2 t+2 x(t)=Cet+t2+2t+2
编写matlab代码:
clc
clear
% 创建一个区域
[t,x] = meshgrid(-2:0.2:3,-1:0.2:2);
% 计算方向向量的斜率
slope = x - t.*t;
% find the length of the vector (1,slope)
length = sqrt(1 + slope .* slope);
% 绘制方向矢量
quiver(t,x,1./length,slope./length,0.5,'Color', '#0072BD')
axis equal equal
hold on
% 给定不同的初值求解析解
tt = [-2:0.2:3];
for cval = -10:1:10
x_exact = cval * exp(tt) + tt.*tt + 2*tt + 2;
plot(tt,x_exact,'Color','#D95319')
end
xlim([-2,3]);
ylim([-1,2]);
xlabel('t','Fontsize',20)
ylabel('x','Fontsize',20)
例子:数值解
还是上面的这个方程,如果我们解不出解析解,那么我们就用数值解来算一下。
d x d t = f ( x , t ) = x − t 2 \frac{d x}{d t}=f(x,t)=x-t^{2} dtdx=f(x,t)=x−t2
使用前向欧拉法的迭代方法:
x
k
+
1
=
x
k
+
h
f
(
x
k
,
t
k
)
x_{k+1}=x_{k}+hf(x_k,t_k)
xk+1=xk+hf(xk,tk)
clc
clear
% 创建一个区域
[t,x] = meshgrid(-2:0.2:3,-1:0.2:2);
% 计算方向向量的斜率
slope = x - t.*t;
% find the length of the vector (1,slope)
length = sqrt(1 + slope .* slope);
% 绘制方向矢量
quiver(t,x,1./length,slope./length,0.5,'Color', '#0072BD')
axis equal equal
hold on
% 给定不同的初值求数值解
tt = [-2:0.2:3];
t_step = 0.2;
k=1;
for x0 = linspace(0.5,2,15)
x_numer(1) = x0;
for t_numer = tt(1:end-1)
k = k + 1;
slope_numer = x_numer(k-1) - t_numer.*t_numer;
x_numer(k) = x_numer(k-1) + slope_numer * t_step;
end
plot(tt,x_numer,'Color','#D95319');
k=1;
end
xlim([-2,3]);
ylim([-1,2]);
xlabel('t','Fontsize',20)
ylabel('x','Fontsize',20)