题解：ABC276E - Round Trip

·题目

链接：Atcoder。

链接：洛谷。

·难度

算法难度：普及。

思维难度：提高。

调码难度：提高。

综合评价：困难。

·算法

bfs。

·思路

从起点周围四个点中任选两个可以走的（记为点1、点2），判断他们两个在不经过起点的情况下是否连通（当然是用bfs判断），由于该两个点之间路径长度至少为2（见图1），所以该回路总长度一定不少于4（起点—{1}—点1—{不少于2}—点2—{1}—起点）。因此，只要有任意两个点可以并经过起点并且互相联通，就应该输出Yes，否则输出No。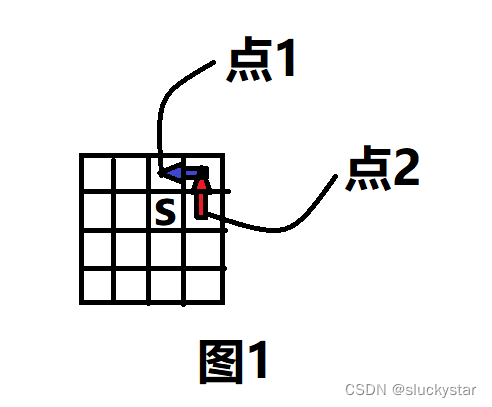

·代价

O(N+M)。

·细节

由于数据大小不确定，对于存储问题可以用vector、string、map等实现。

·代码

#include<bits/stdc++.h>
#define N 1100000
using namespace std;
struct Node{
    int d,x,y;
};
map<pair<int,int>,bool>see;
string mp[N]={};
Node q[N]={};
int c[4][2]={{-1,0},{0,-1},{0,1},{1,0}},h=0,w=0,x=0,y=0;
char in[N]={};
bool can_get(int ax,int ay,int bx,int by);
int main(){
    scanf("%d%d",&h,&w);
    for(int i=1;i<=h;i++){
        scanf("%s",in);
        mp[i]=in;
    }
    for(int i=1;i<=h;i++){
        mp[i]=' '+mp[i];
        for(int j=1;j<=w;j++){
            if(mp[i][j]=='S'){
                x=i;
                y=j;
            }
        }
    }
    for(int i=0;i<4;i++){
        for(int j=i+1;j<4;j++){
            int ax=x+c[i][0],ay=y+c[i][1],bx=x+c[j][0],by=y+c[j][1];
            if(mp[ax][ay]!='#'&&mp[bx][by]!='#'){
                if(can_get(ax,ay,bx,by)==true){
                    printf("Yes\n");
                    return 0;
                }
            }
        }
    }
    printf("No\n");
    return 0;
}
bool can_get(int ax,int ay,int bx,int by){
    see.clear();
    int front=1,rear=0;
    rear++;
    q[rear]={0,ax,ay};
    see[{ax,ay}]=true;
    while(front<=rear){
        Node now=q[front];
        if(now.x==bx&&now.y==by){
            return true;
        }
        for(int i=0;i<4;i++){
            int nx=now.x+c[i][0],ny=now.y+c[i][1];
            if(see[{nx,ny}]==true||nx<1||ny<1||nx>h||ny>w||nx==x&&ny==y||mp[nx][ny]=='#'){
                continue;
            }else{
                see[{nx,ny}]=true;
                rear++;
                q[rear]={now.d+1,nx,ny};
            }
        }
        front++;
    }
    return false;
}