栈和队列的应用

---

目录

 栈和队列的应用

一、括号匹配（栈）

二、表达式的各种转换

(1)中缀转后缀(手工)

(2)后缀转中缀表达式(手工)

(3)中缀转后缀(栈)

(4)中缀转后缀（树）

(5)后缀表达式求值

(6)中缀表达式求值（栈）

三、栈在递归的应用

四、队列的应用

一、括号匹配（栈）

        思想：括号匹配就是有() [] {},各种各样的括号，符合相应匹配的括号正确，否则为非法情况。

        主要利用栈，给括号凑存入数组中。然后读取，当读取左括号时，入栈，当遇到右括号时，栈内出栈，与之对比，若匹配则继续扫描数组，否则则非法，程序结束，非法情况除了括号不对应外，还有，两种，一个是扫到右括号，去栈内拿括号，结果栈空了。另一种则是栈内还有括号，但是数组已经读取完了。

        代码如下：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
//创建栈
typedef struct
{
	char data[50];
	int top;	
}SqStack;
void InitStack(SqStack *s)
{
	s->top=-1;	
}
//入栈 
void StackPush(SqStack *s,char x)
{
	s->top++;
	s->data[s->top]=x;
}
//出栈
void StackPop(SqStack *s,char *e)
{
	if(s->top == -1)
	{
		printf("栈都空了，没东西了\n");
		exit(-1);
	}
	
	*e =s->data[s->top];
	s->top--;			
}
void  KuohaoMatch(char *num,int len)
{
	SqStack s;
	InitStack(&s);
	int i;
	for(i=0;i<len;i++)
	{
		if(num[i]=='(' || num[i]=='[' || num[i]== '{') 
		StackPush(&s,num[i]);
		else
		{
			if(s.top== -1)
			{
				printf("栈内没有匹配的括号，匹配失败\n"); 
				exit(-1);
			}
			char e='a';
			StackPop(&s,&e);
			
			if(num[i]=='}' && e != '{') 
			{
				printf("}匹配失败\n");
				exit(-1);
			}
			if(num[i]==']' && e != '[') 
			{
				printf("]匹配失败\n");
				exit(-1);
			}
			if(num[i]==')' && e != '(') 
			{
				printf(")匹配失败\n");
				exit(-1);
			}
		}
	} 
	if(s.top==-1)
	printf("匹配完毕，未发现异常，匹配成功\n");
	else
	printf("栈内仍有括号，匹配失败\n"); 
	
}

int main()
{
	char num[10]="{([])}";
	int len=strlen(num);
	KuohaoMatch(num,len);
	
	return 0;
}

二、表达式的各种转换

       表达式，根据操作符的位置，有不同的叫法，如a+b，为中缀，因为+在中间。同理+ab为前缀，ab-为后缀。

        我们日常见到的为中缀表达式，但如果让计算机识别的话，比较费劲，因此我们如果给中缀表达式转化为后缀表达式（当计算机遇到两个操作数和一个操作算符就会直接计算）或前缀表达式（当计算机遇到一个操作算符和两个操作数就会直接计算），这计算机就可直接进行计算，

(1)中缀转后缀(手工)

        如：A+B*(C-D)-E/F.

由于同级操作算符，中缀可以转不同的后缀表达式，不唯一，

两种计算方法：
        方法一：我们可以根据优先级，一块一块的去算，先计算（C-D）为CD-，E/F为EF/，而B*（CD-）也是两操作数，因此为BCD-*,随后A+（BCD-*）为两个操作数，所以ABCD-*+，最后（ABCD-*+）-（EF/）为两个操作数，因此为：ABCD-*+EF/-.

 方法二：从左至右书写字符，按照优先级，如果能计算，优先计算，

(2)后缀转中缀表达式(手工)

        后缀表达式则跟中缀思想差不多，也是块思想，每一个小的操作计算，都是一小块一个整体，又内向外，逐层计算。

 注意：变为中缀，要根据优先级，加括号记得，此外由后缀转中缀，结果唯一。

(3)中缀转后缀(栈)

        之前是手工草稿推的，一般选择填空应用，够用了，不过如果，要求按照栈的思想，去实现中缀转后缀，则需要学一下这个。

        大致思想：遍历到字符，直接输出，遍历到操作符，给它入栈，如果又遇到操作符，便与栈顶的操作符对比，如果栈顶的操作符优先级高，则给栈顶弹出，优先级低的，入栈。此外遇到（），先入（，之后遇见）,则给栈内（之前的内容都弹出。

        

(4)中缀转后缀（树）

即给表达式，写成树的形式，其中根节点为符号，每一棵树为一个小计算整体，此外选每颗树的根时，先理清楚计算先后，以及整体。

        给中缀先转化成树的形式。

根据计算优先级，划分括号，然后再原意义一样的情况下，组成树。最开始的根节点为操作符。

如：A+B*(C-D)-E/F

 

 

 

        给出表达式树，求中缀或前缀，后缀表达式：

给每个结点表上1 2 3，然后从最上层开始画线，跑一圈，其中1代表前缀，2中缀，3后缀

(5)后缀表达式求值

        利用栈的大致思想：给操作数入栈，遇到操作符，从栈中弹出两个数，进行计算，计算结果，接着入栈。依次类推。

最后几步，类似这样，一直弄完，

手工求解。

方法一：可先给后缀表达为中缀，（画框法，没每一个小块先转换，由内向外逐层转换）

方法二：遇到两个操作数和一个操作符，三者挨着的，优先计算，依次类推。前缀一样思想

 

(6)中缀表达式求值（栈）

创建两个栈，一个栈存操作符，一个栈存操作数，

当识别到操作符，并且比操作符栈顶操作符优先级小时，弹出两个数，进行计算，并入字符数栈。

优先级相同时，遵循最左原则，操作符栈内的优先计算，

如：3*（7-2），另外，进行栈求的时候，需要给表达式两边加上#号。

#3*(7-2)#

操作符栈：#  *  ( - 

操作数栈：3  7   2 

栈内-比）优先级高，-弹出，7 2 弹出，计算，7-2=5，5入数栈，另外计算减法时，按照原本意义计算，不能减反了

操作符栈：#  *  

操作数栈：3  5

栈内*比栈外，#优先级高，*弹出，3 5 弹出，计算3*5=15，15入栈

操作符栈：##

操作数栈：15

#检测到与它相等的#，程序结束。

三、栈在递归的应用

        这里即递归的意义。

        递归就是在系统栈中，开辟临时空间，进行操作。逐层创建内推，到最内层的结束条件时，再往回返回。

四、队列的应用

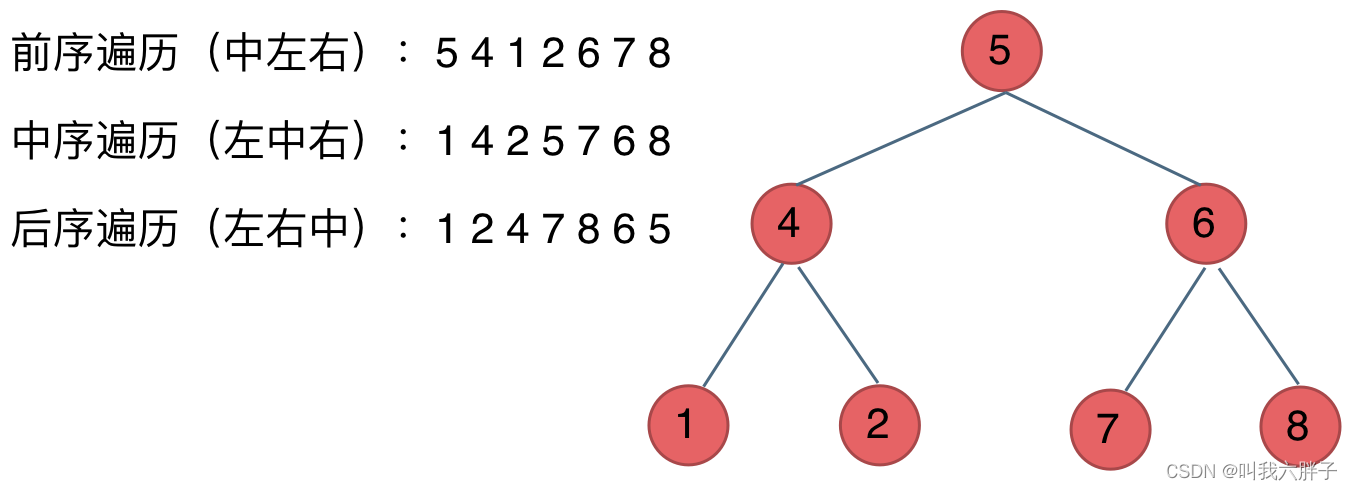
二叉树层次遍历，

        从上而下，从左至右，一个树一个树的进行，每次遍历都是入队，然后从对头挨个处理即可！