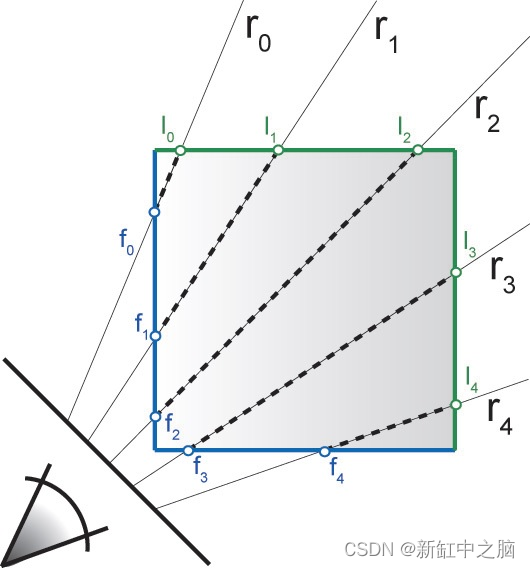
一、下一个更大元素II
链接:力扣
描述如下:给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。

思路如下:
分两个思路,就是将原数组进行拼块,两个拼一起。还有就是处理循环数组。将两个nums数组拼接在一起,使用单调栈计算出每一个元素的下一个最大值,最后再把结果集即result数组resize到原数组大小就可以了。
循环数组的处理方式:

代码如下:
第一种思路:
class Solution {
public:
//需要去遍历成环的数组,将两个数组合起来
//可采用扩展数组的方式来实现
vector<int> nextGreaterElements(vector<int>& nums)
{
//存放结果
vector<int>result(2*nums.size(),-1);
vector<int>temp(nums.begin(), nums.end());//扩展后的数组
for (int i = 0; i < nums.size(); i++)
{
temp.push_back(nums[i]);
}
stack<int>st;//单调栈
st.push(0);
for (int i = 1; i < temp.size(); i++)
{
if (temp[i] < temp[st.top()])
{
st.push(i);
}
else if (temp[i] == temp[st.top()])
{
st.push(i);
}
else
{
while (!st.empty() && temp[st.top()] < temp[i])
{
int index = st.top();
result[index] = temp[i];
st.pop();
}
}
st.push(i);
}
result.resize(nums.size());
return result;
}
};第二种思路:
class Solution {
public:
//需要去遍历成环的数组,将两个数组合起来
//可采用扩展数组的方式来实现
vector<int> nextGreaterElements(vector<int>& nums)
{
//不用扩充数组的方式
stack<int>st;//单调栈
vector<int>result(nums.size(), -1);
st.push(0);
for (int i = 1; i < 2 * nums.size(); i++)
{
int index = st.top();
if (nums[i%nums.size()] < nums[index])
{
st.push(i % nums.size());
}
else if (nums[i % nums.size()] == nums[index])
{
st.push(i % nums.size());
}
else
{
while (!st.empty() && nums[i % nums.size()] > nums[st.top()])
{
result[st.top()] = nums[i % nums.size()];
st.pop();
}
st.push(i % nums.size());
}
}
return result;
}
};运行如下:
二、接雨水
链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
描述如下:给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

思路如下:
接雨水这道题目,需要寻找一个元素,右边最大元素以及左边最大元素,来计算雨水面积。
本题使用单调栈有如下几个问题:
1、首先单调栈是按照行方向来计算雨水,如图:

2、使用单调栈内元素的顺序
从大到小还是从小到大呢?从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
如图:
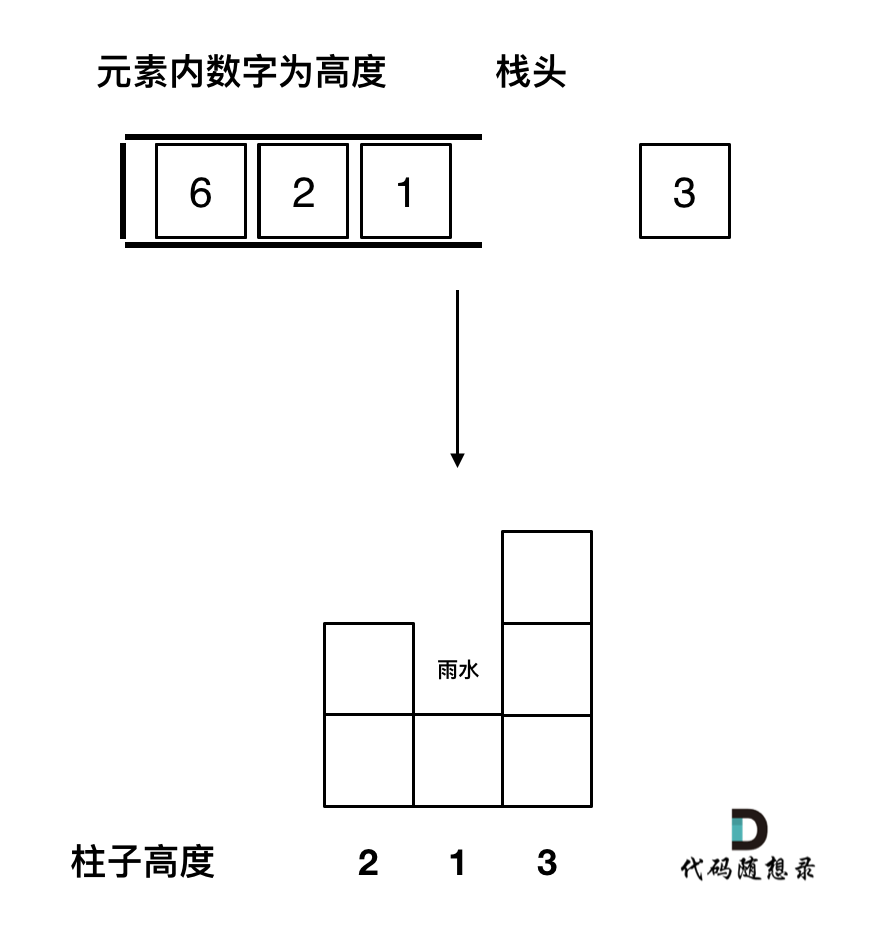
3、遇到相同高度的柱子怎么办。
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
因为要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
如图所示:
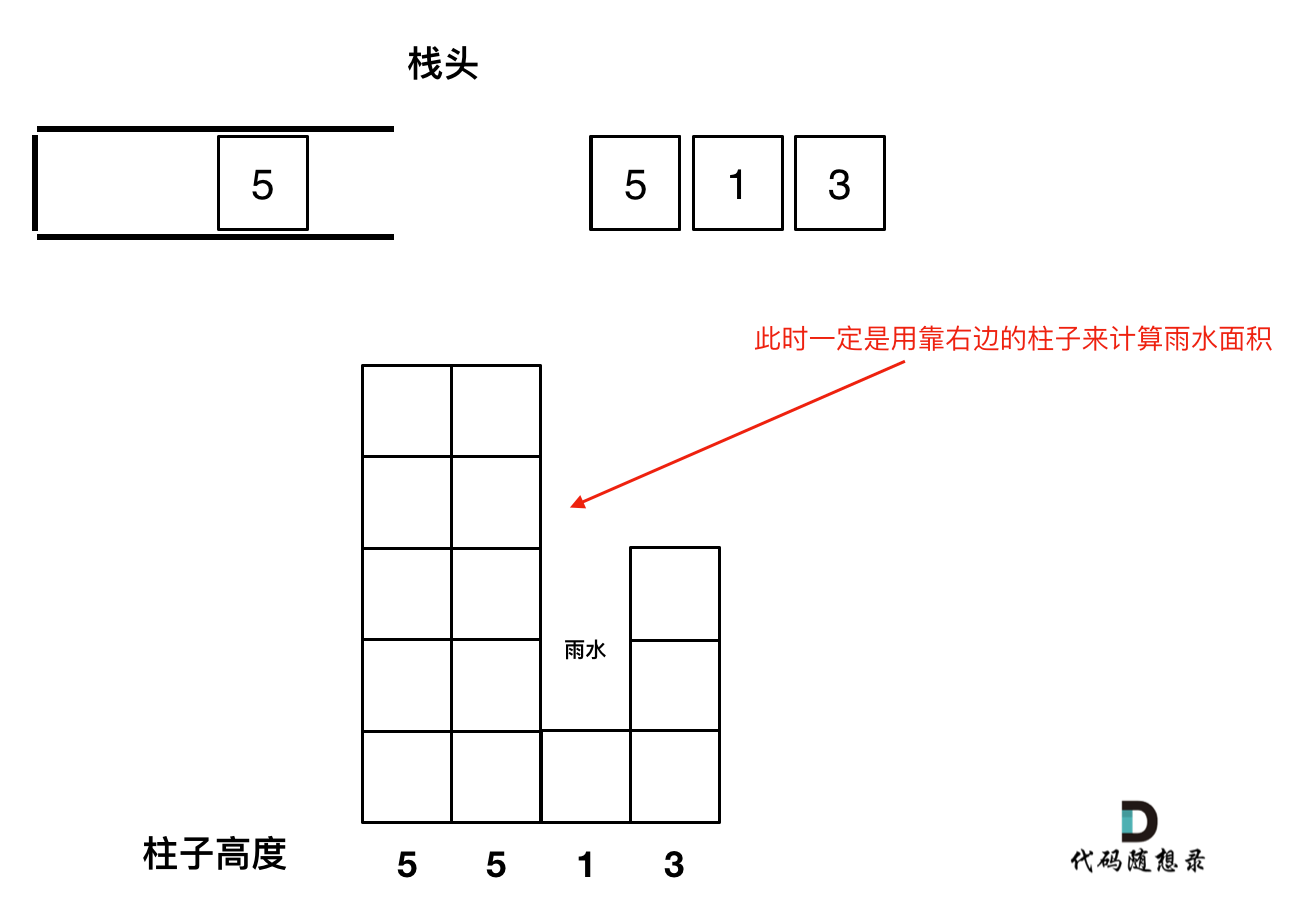
4、栈里要保存什么数值
使用单调栈,也是通过 长 * 宽 来计算雨水面积的。
长就是通过柱子的高度来计算,宽是通过柱子之间的下标来计算,栈里就存放下标就行,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下标对应的高度了。
所以栈的定义如下:
stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度
以下逻辑主要就是三种情况
- 情况一:当前遍历的元素(柱子)高度小于栈顶元素的高度 height[i] < height[st.top()]
- 情况二:当前遍历的元素(柱子)高度等于栈顶元素的高度 height[i] == height[st.top()]
- 情况三:当前遍历的元素(柱子)高度大于栈顶元素的高度 height[i] > height[st.top()]
先将下标0的柱子加入到栈中,st.push(0);。 栈中存放遍历过的元素,所以先将下标0加进来。
然后开始从下标1开始遍历所有的柱子,for (int i = 1; i < height.size(); i++)。
如果当前遍历的元素(柱子)高度小于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从小到大的顺序(从栈头到栈底)。
代码如下:
if (height[i] < height[st.top()]) st.push(i);
如果当前遍历的元素(柱子)高度等于栈顶元素的高度,要跟更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度。
代码如下:
else if (height[i] == height[st.top()]) {
st.push(i);
}
如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
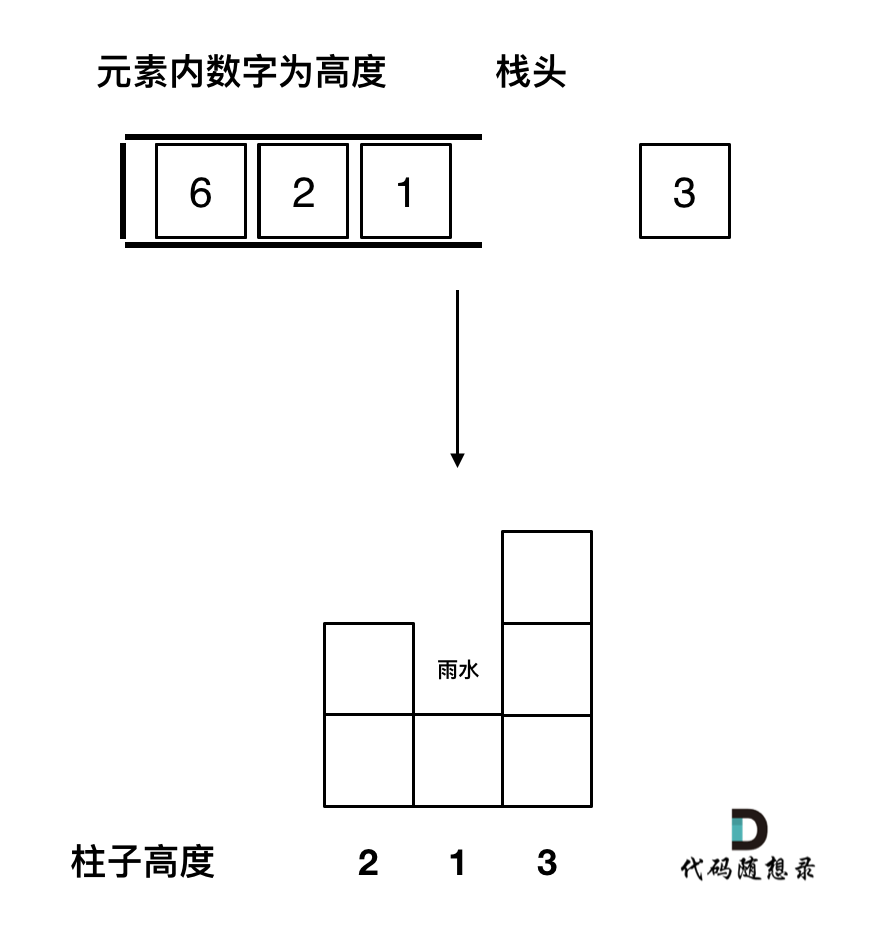
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
此时的栈顶元素st.top(),就是凹槽的左边位置,下标为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
当前遍历的元素i,就是凹槽右边的位置,下标为i,对应的高度为height[i](就是图中的高度3)。
可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的元素,三个元素来接水!
那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:int h = min(height[st.top()], height[i]) - height[mid];
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:int w = i - st.top() - 1 ;
当前凹槽雨水的体积就是:h * w。
求当前凹槽雨水的体积代码如下:

代码如下:
class Solution {
public:
int trap(vector<int>& height)
{
if (height.size() == 0)
{
return 0;
}
stack<int>st;//单调栈
st.push(0);
int result = 0;//记录雨水的面积
for (int i = 1; i < height.size(); i++)
{
if (height[st.top()] > height[i])
{
st.push(i);
}
if (height[st.top()] == height[i])
{
st.push(i);
}
else
{
//记录中间位置
while (!st.empty() && height[st.top()] < height[i])
{
int mid = st.top();
st.pop();//弹出取左边第一个比中间元素大的元素
if (!st.empty())
{
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1;//宽度
result += h * w;
}
}
st.push(i);
}
}
return result;
}
};运行如下: