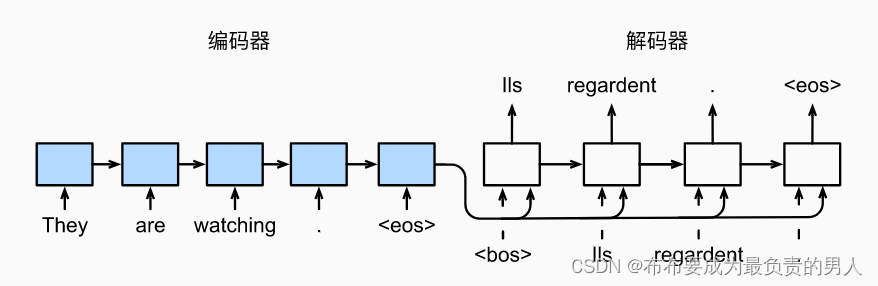
这节课我们主要学习一下(Linear Independence)线性无关,(spanning a space)生成空间,(basis)基和(dimension)维度。同时我们要注意这四个很重要的基本概念的描述对象,我们会说向量组线性无关,由一个向量组生成的空间,子空间的基是一组向量组,但我们不会用这些词来修饰矩阵,至于维度则是一个数值,他是用于描述空间的维度,如列空间的维度,零空间的纬度,而不适用于描述矩阵。我们现在只会用矩阵的秩和主列的个数来描述矩阵。

x.1 Linear independence
我们首先给出(Linear independence)线性无关的定义:给定一组向量组,如果我们能找不到一组不全为0的数c1,c2…cn使得c1x1+c2x2+…+cnxn=0成立,则向量组线性无关。若找到线性组合系数,则线性相关。
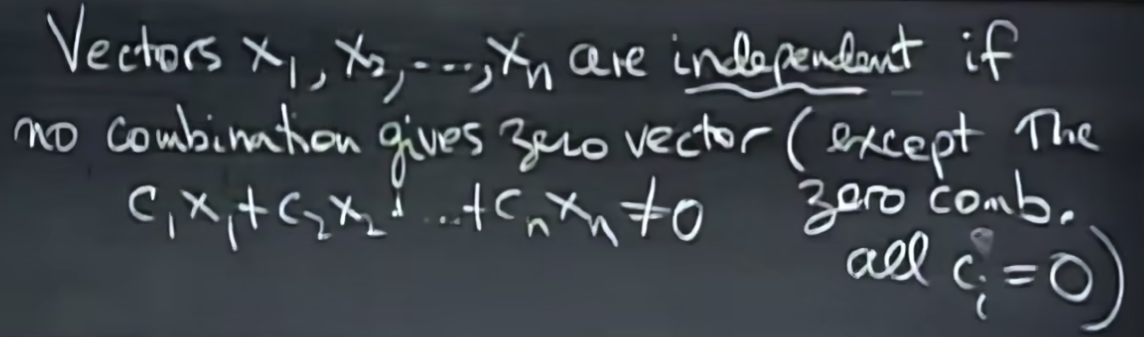
接下来我们结合画图来理解下,假如在R2二维空间中,两个向量共线则易见相关,
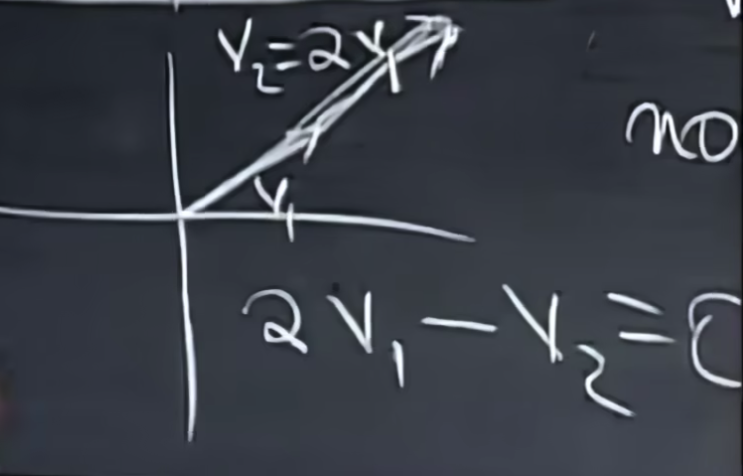
若向量组中存在零向量,则一定相关,
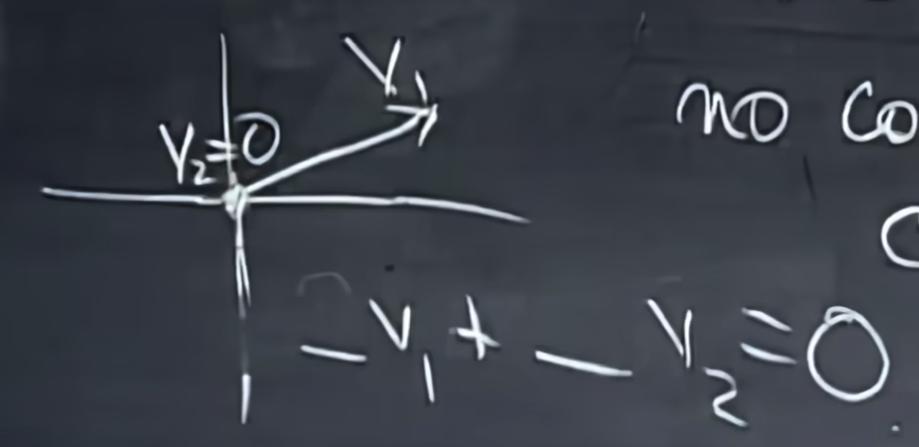
下面这个则是线性无关,
但是三个向量则一定线性相关,那这是为什么呢?接下来,我们会将线性相关性和方程组求解,以及矩阵联系起来。我们在先前已经将方程组求解和矩阵联系起来过了。

我们将向量组以列向量的方式表示,化为矩阵A,我们发现这是一个自由度为3,约束条件为2的方程组,易于发现他是存在自由列的,
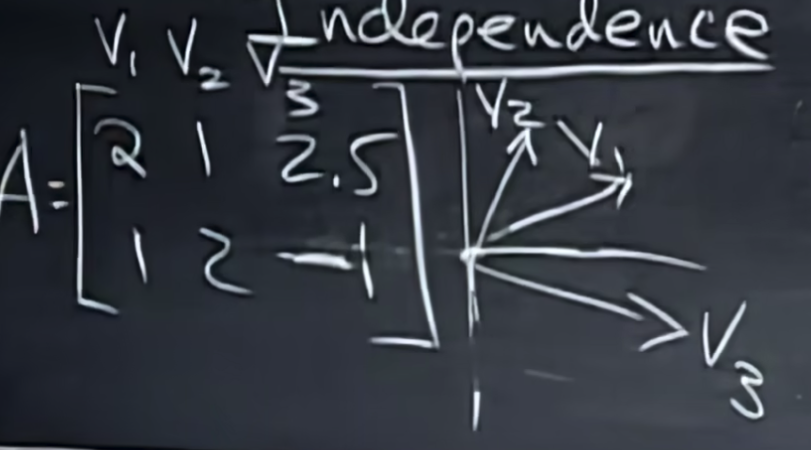
我们将线性无关和Ax=0零空间求解联系起来,我们得到如下定义:由列向量组组成的矩阵A,如果A的零空间只有零向量则向量组线性无关,如果零空间还有别的非零向量则向量组线性相关。
换言之,如果矩阵A满秩,即rank=r,即没有自由变量则线性无关;如果矩阵A不满秩,即rank<r,即有自由变量则线性相关。

x.2 Span a Space
对于生成一个空间,给定的定义如下:对于向量组v1,…,vn生成一个空间,即指这个空间包含这些向量的所有线性组合。
例如列空间即是由矩阵A的所有列向量生成的空间。
x.3 Basis
对于基的定义如下:对于向量组v1,…,vn他们首先是线性无关的;其他他们生成了一个空间。那么对于这个空间,它的基就是这一组向量组。
首先我们需要知道对于一个空间,构成他们的基的个数永远是相同的。即如果一个空间由3个基构成,如果你有3个线性无关的向量,则这3个向量构成的向量组就是这个空间的基。
基并不唯一,有无数多个。
x.4 Dimension
维数定义:基的个数即空间的维数。
所有我们有了一个重要性质,对于矩阵A,矩阵A的秩r=主列的个数=A的列空间的维数。
对于矩阵A,矩阵A的自由变量数n-r=自由列的个数=A的零空间的维数。